2023-2024学年海南省澄迈县八年级（下）期末数学试卷（含答案）

展开

这是一份2023-2024学年海南省澄迈县八年级（下）期末数学试卷（含答案），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.使 x−2024有意义的x的取值范围是( )
A. x>2024B. x<−2024C. x≤2024D. x≥2024
2.下列运算中，正确的是( )
A. 22=2B. ± 9=3C. 16=8D. (−2)2=−2
3.若点A(−5,y1)，B(1,y2)都在直线y=2x+7上，则y1与y2的大小关系是( )
A. y1y2D. 无法比较大小
4.一次函数y=kx+b(k≠0，k,b为常数)的图象如图所示，则k,b的取值范围是( )
A. k>0,b>0B. k<0,b>0C. k>0,b<0D. k<0,b<0
5.菲尔兹奖(Fields Medal)是数学领域的国际最高奖项之一，每四年颁发一次，每次授予2至4名有卓越贡献的数学家.下面数据是部分获奖者获奖时的年龄(单位：岁)：32，35，29，33，40，35，则这组数据的众数是( )
A. 29B. 32C. 33D. 35
6.甲、乙、丙三个旅行团的游客人数相等，且平均年龄都是32岁，游客年龄的方差分别是S甲2=27，S乙2=19.6，S丙2=8.6，导游小王最喜欢带游客年龄相近的团，则他应选( )
A. 甲团B. 乙团C. 丙团D. 无法确定
7.如图，平面直角坐标系中，点A，B的坐标分别为(0,6)，(8,0)，以点A为圆心，AB长为半径画弧，交y轴负半轴于点C，则点C的坐标为( )
A. (−10,0)
B. (0,−10)
C. (0,−2)
D. (0,−4)
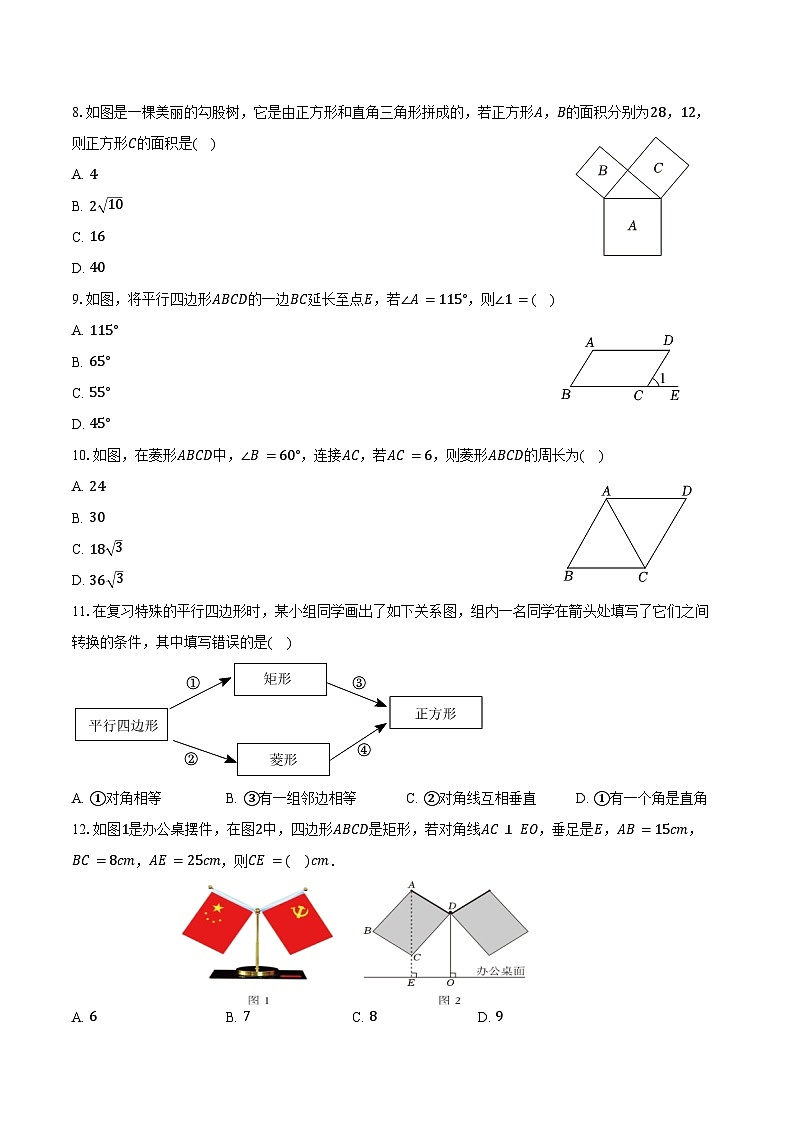
8.如图是一棵美丽的勾股树，它是由正方形和直角三角形拼成的，若正方形A，B的面积分别为28，12，则正方形C的面积是( )
A. 4
B. 2 10
C. 16
D. 40
9.如图，将平行四边形ABCD的一边BC延长至点E，若∠A=115°，则∠1=( )
A. 115°
B. 65°
C. 55°
D. 45°
10.如图，在菱形ABCD中，∠B=60°，连接AC，若AC=6，则菱形ABCD的周长为( )
A. 24
B. 30
C. 18 3
D. 36 3
11.在复习特殊的平行四边形时，某小组同学画出了如下关系图，组内一名同学在箭头处填写了它们之间转换的条件，其中填写错误的是( )
A. ①对角相等B. ③有一组邻边相等 C. ②对角线互相垂直D. ①有一个角是直角
12.如图1是办公桌摆件，在图2中，四边形ABCD是矩形，若对角线AC⊥EO，垂足是E，AB=15cm，BC=8cm，AE=25cm，则CE=( )cm．
A. 6B. 7C. 8D. 9
二、填空题：本题共4小题，每小题3分，共12分。
13.计算： 5× 10÷ 12= ______．
14.某校举办了以“展礼仪风采，树文明形象”为主题的比赛.已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为90分，80分，80分，若依次按照30%，45%，25%的百分比确定成绩，则该选手的成绩是______分.
15.如图所示，在正方形ABCD中，若对角线的长为10cm，P是CD上任意一点，过点P分别作PE⊥BD，PF⊥AC，垂足分别为E，F，则PE+PF= ______cm．
16.如图，▱ABCD中，AB=3，BC=4，BE平分∠ABC，交AD于点E，CF平分∠BCD，交AD于点F，交BE于点O，点G，H分别是OF和OE的中点，则AE=DF= ______，GH= ______．
三、解答题：本题共6小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题12分)
计算：(1) 2+ 8−(13)−1+|−3|；
(2)( 5+ 2)( 5− 2)+( 5−1)2．
18.(本小题10分)
八年级二班小明和小亮同血学习了“勾股定理”之后，为了测得得如图风筝的高度CE，
他们进行了如下操作：
(1)测得BD的长度为15米．(注：BD⊥CE)
(2)根据手中剩余线的长度计算出风筝线BC的长为25米．
(3)牵线放风筝的小明身高1.6米．
求风筝的高度CE．
19.(本小题10分)
科学教育是提升国家科技竞争力、培养创新人才、提高全民科学素质的重要基础，某学校计划在八年级开设“人工智能”“无人机”“创客”“航模”四门校本课程，要求每人必须参加，并且只能选择其中一门课程，为了解学生对这四门课程的选择情况，学校从八年级全体学生中随机抽取部分学生进行问卷调查，并根据调查结果绘制成如图1和2所示的条形统计图和扇形统计图(部分信息未给出)．

请你根据以上信息解决下列问题：
(1)参加问卷调查的学生人数为______名，补全条形统计图(画图并标注相应数据)；
(2)在扇形统计图中，选择“创客”课程的学生占______%，所对应的圆心角度数为______；
(3)若该校八年级一共有1000名学生，试估计选择“航模”课程的学生有多少名？
20.(本小题12分)
“黄金8号”玉米种子的价格5元/kg，如果一次购买10kg以上的种子，超过10kg部分的种子价格打8折．
(1)购买8kg种子需付款______元；购买13kg种子需付款______元．
(2)设购买种子x(x>10)kg，付款金额为y元，写出y与x之间的函数关系式．
(3)张大爷第一次买了6kg种子，第二次买了9kg种子．如果张大爷一次性购买种子，会少花多少钱？
21.(本小题13分)
如图，在四边形ABCD中，AB//DC，AB=CD，对角线AC，BD交于点O，过点C作CE⊥AB交AB的延长线于点E，且∠ABO=∠ACE，连接OE．
(1)求证：四边形ABCD是菱形；
(2)若AB=2 10，BD=4，求OE的长．
22.(本小题15分)
如图，在平面直角坐标系中，直线AB与x轴、y轴相交于A(4,0)，B(0,2)两点，点C在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，点D恰好落在直线AB上，过点D作DE⊥x轴于点E．
(1)求直线AB的函数表达式；
(2)求证：△BOC≌△CED；
(3)点D的坐标为：______，△BCD的面积为______；
(4)在平面内是否存在点Q，使以B、C、D、Q为顶点的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，请说明理由．
参考答案
1.D
2.A
3.A
4.C
5.D
6.C
7.D
8.C
9.B
10.A
11.A
12.C
13.10
14.83
15.5
16.3 1
17.解：(1) 2+ 8−(13)−1+|−3|
= 2+2 2−3+3
=3 2；
(2)( 5+ 2)( 5− 2)+( 5−1)2
=5−2+5−2 5+1
=9−2 5．
18.解：在Rt△CDB中，
由勾股定理得，CD2=BC2−BD2=252−152=400，
所以，CD=±20(负值舍去)，
所以，CE=CD+DE=20+1.6=21.6米，
答：风筝的高度CE为21.6米．
19.(1)由题知，
问卷调查的学生中选择“无人机”课程的学生人数为15，且所占百分比为30%，
所以15÷30%=50(名)，
即问卷调查的学生人数为50名．
所以选择“人工智能”课程的学生人数为：50−15−10−5=20(名)，
条形统计图，如图所示，
．
(2)20，72°．
(3)1000×550=100(名)，
答：选择“航模”课程的学生有100名．
20.(1)40，62；
(2)y与x之间的函数关系式为：
y=10×5+5×80%⋅(x−10)=50+4x−40=4x+10(x>10)；
(3)第一次买了6kg种子付款金额为6×5=30(元)，
第二次买了9kg种子付款金额为9×5=45(元)，
一次性购买种子付款金额为4×15+10=70(元)，
∴会少花30+45−70=5(元)
答：如果张大爷一次性购买种子，会少花5元钱．
21.(1)证明：∵CE⊥AB，
∴∠CEA=90°，
∴∠CAE+∠ACE=90°，
∵∠ABO=∠ACE，
∴∠ABO+∠BAO=90°，
∴∠AOB=90°，
∴AO⊥OB，
∵AB//CD，AB=CD，
∴四边形ABCD是平行四边形，
又∵AC⊥BD，
∴平行四边形ABCD是菱形；
(2)解：∵四边形ABCD是菱形，BD=4，
∴OA=OC，BD⊥AC，OB=OD=2，
∴∠AOB=90°，
∴OA= AB2−OB2= 40−4=6，
∴AC=2OA=12，
∵CE⊥AB，
∴OE=12AC=6．
22.(1)解：设直线AB解析式为y=kx+b，把A(4,0)，B(0,2)代入上式得：
0=4k+bb=2，
解得k=−12b=2，
故直线AB的解析式为y=−12x+2；
(2)证明：∵∠BOC=∠BCD=∠CED=90°，
∴∠OCB+∠DCE=90°，∠DCE+∠CDE=90°，
∴∠BCO=∠CDE，
在△BOC与△CED中，
∠BOC=∠CED∠BCO=∠CDEBC=CD，
∴△BOC≌△CED(AAS)；
(3)(83,23)，209；
(4)解：∵D(83,23)，B(0,2)，C(23,0)，
∴存在点Q，使以B、C、D、Q为顶点的四边形是平行四边形，
当BD为平行四边形的边时，可得Q1(−2,43)，Q2(103,−43).
当BD为对角线时，可得Q3(2,83).
综上所述，满足条件的点Q的坐标为(−2,43)或(103,−43)或(2,83).