




初中数学湘教版九年级上册4.4 解直接三角形的应用课文ppt课件
展开1.理解并掌握坡度的定义.2.学会用坡度解决实际问题.(重点、难点)
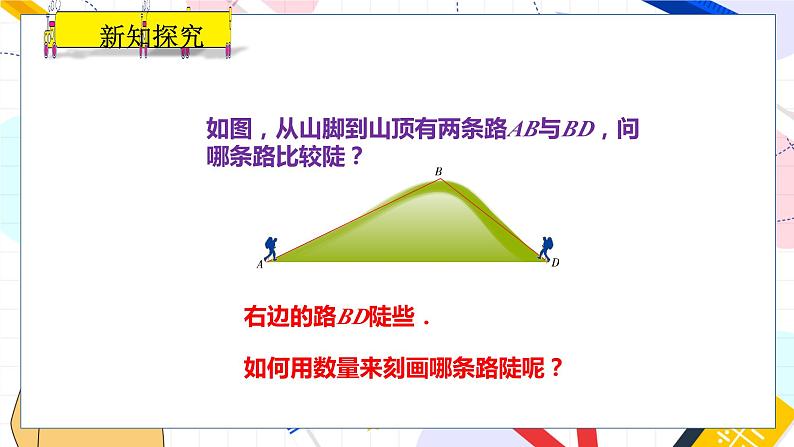
如图,从山脚到山顶有两条路AB与BD,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
如上图所示,从山坡脚下点 A 上坡走到点B时,升高的高度h(即线段BC的长度)与水平前进的距离l(即线段AC 的长度)的比叫作坡度,用字母i表示,即
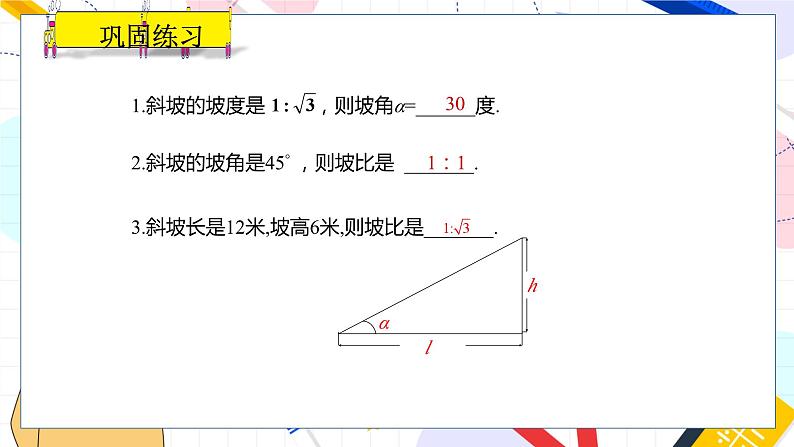
1.斜坡的坡度是 ,则坡角α=______度.2.斜坡的坡角是45° ,则坡比是 _______.3.斜坡长是12米,坡高6米,则坡比是_______.
如图,在Rt△ABC中,∠B=90°,∠A=26.57°,AC=240m,
答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.
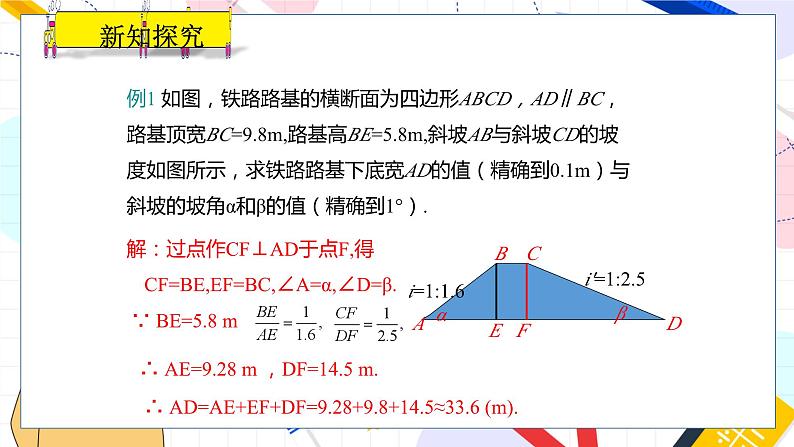
例1 如图,铁路路基的横断面为四边形ABCD,AD∥BC,路基顶宽BC=9.8m,路基高BE=5.8m,斜坡AB与斜坡CD的坡度如图所示,求铁路路基下底宽AD的值(精确到0.1m)与斜坡的坡角α和β的值(精确到1°).
解:过点作CF⊥AD于点F,得
CF=BE,EF=BC,∠A=α,∠D=β.
∵ BE=5.8 m
∴ AE=9.28 m ,DF=14.5 m.
∴ AD=AE+EF+DF=9.28+9.8+14.5≈33.6 (m).
与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢?
我们设法“化曲为直,以直代曲”. 我们可以把山坡“化整为零”地划分为一些小段,如图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角a1,这样就可以算出这段山坡的高度h1=l1sina1.
在每小段上,我们都构造出直角三角形,利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,然后我们再“积零为整”,把h1,h2,…,hn相加,于是得到山高h.
以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,它在数学中有重要地位,在今后的学习中,你会更多地了解这方面的内容.
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识. 例如,当我们要测量如图所示大坝的高度h时,只要测出仰角a和大坝的坡面长度l,就能算出h=lsina,但是,当我们要测量如图所示的山高h时,问题就不那么简单了,这是由于不能很方便地得到仰角a和山坡长度l.
化整为零,积零为整,化曲为直,以直代曲的解决问题的策略
引例 如图,一船以40km/h的速度向东航行,在A处测得灯塔C在北偏东60°方向上,继续航行 1 h 到达B处,再测得灯塔C在北偏东30°方向上.已知灯塔C四周30km 内有暗礁,问这艘船继续向东航行,是否安全?
与方位角有关的实际问题
【分析】这船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于 30km .
解:由点C作CD⊥AB,
设CD= x km,
所以,这船继续向东航行是安全的.
由AB=AD-BD,得
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?
解:如图 ,在Rt△APC中,
PC=PA·cs(90°-65°)
在Rt△BPC中,∠B=34°
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130.23海里.
利用解直角三角形的知识解决实际问题的一般过程是:(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;(3)得到数学问题的答案;(4)得到实际问题的答案.
例2 一条东西走向的高速公路上有两个加油站A,B,在A的北偏东45°方向还有一个加油站C,C到高速公路的最短距离是30km,B,C间的距离是60km,想要经过C修一条笔直的公路与高速公路相交,使两路交叉口P到B,C的距离相等,请求出交叉口P到加油站A的距离(结果保留根号).
分析:此题针对点P的位置分两种情况讨论,即点P可能在线段AB上,也可能在BA的延长线上.
解:分两种情况:(1)如图①,在Rt△BDC中,CD=30km,BC=60km,∴∠B=30°.∵PB=PC,∴∠BCP=∠B=30°.∴在Rt△CDP中,∠CPD=∠B+∠BCP=60°.
在Rt△ADC中,∵∠A=45°,∴AD=DC=30km.
(2)如图②,同理可求得 km,AD=30km.
求一般三角形的边长或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
1.如图,某水库堤坝横断面迎水坡AB的坡度是1: ,堤坝高BC=50m,则迎水坡面AB的长度是( )
B.100 m
D.50 m
2.如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于 .
3.一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽(精确到0.1米, ).
初中数学冀教版九年级上册26.4 解直角三角形的应用多媒体教学课件ppt: 这是一份初中数学冀教版九年级上册<a href="/sx/tb_c107219_t3/?tag_id=26" target="_blank">26.4 解直角三角形的应用多媒体教学课件ppt</a>,共13页。PPT课件主要包含了解直角三角形的应用,坡度问题,坡度或坡比等内容,欢迎下载使用。
初中数学湘教版九年级上册4.3 解直角三角形作业课件ppt: 这是一份初中数学湘教版九年级上册4.3 解直角三角形作业课件ppt,共53页。
初中数学湘教版九年级上册4.4 解直接三角形的应用教学ppt课件: 这是一份初中数学湘教版九年级上册4.4 解直接三角形的应用教学ppt课件,文件包含湘教版数学九年级上册442与坡度坡角有关的实际问题pptx、第2课时与坡度坡角有关的实际问题doc等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。












