数学九年级上册5 相似三角形判定定理的证明课前预习课件ppt

这是一份数学九年级上册5 相似三角形判定定理的证明课前预习课件ppt，共33页。PPT课件主要包含了课前预习，典例讲练等内容，欢迎下载使用。

数学 九年级上册 BS版
三角形相似的判定定理.（1）定理一： ⁠；（2）定理二： ⁠；（3）定理三： ⁠.
两角分别相等的两个三角形相似　
两边成比例且夹角相等的两个三角形相似　
三边成比例的两个三角形相似　
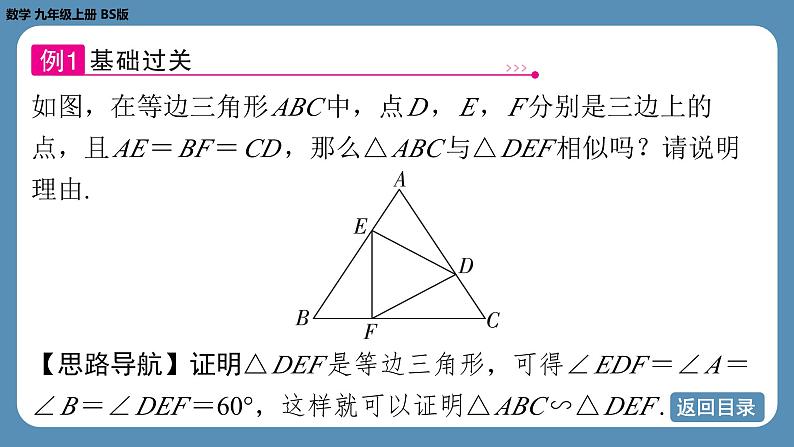
如图，在等边三角形 ABC 中，点 D ， E ， F 分别是三边上的 点，且 AE ＝ BF ＝ CD ，那么△ ABC 与△ DEF 相似吗？请说明 理由.
【思路导航】证明△ DEF 是等边三角形，可得∠ EDF ＝∠ A ＝ ∠ B ＝∠ DEF ＝60°，这样就可以证明△ ABC ∽△ DEF .
【点拨】在等边三角形三边上取三点，截取三条相等线段，无 论三截点怎么变化，截出的含顶角的三个小三角形都全等，中 间小三角形一定是等边三角形.特别地，若截点是各边中点，则 四个三角形都是等边三角形.
如图，在Rt△ ABC 中，已知∠ ACB ＝90°， CD ⊥ AB 于点 D ，分 别以 AC ， BC 为边向三角形外部作等边三角形 ACE 和等边三角 形 BCF ，连接 DE ， DF . 证明：△ ADE ∽△ CDF .
证明：∵四边形 ABCD 是正方形，∴ AB ＝ BC ，∠ DAB ＝90°.∴∠ GBA ＋∠ AEG ＝90°.∵ AG ⊥ BE ，∴∠ EGA ＝∠ AGB ＝90°.∴∠ EAG ＋∠ AEG ＝90°.∴∠ EAG ＝∠ GBA . ∴△ AGE ∽△ BGA .
【点拨】当无法证明“比例式”或“等积式”线段所在的两个 三角形相似时，可以考虑“等线段替换”或者“等比替换”， 将问题进行转化.
如图，在菱形 ABCD 中，已知∠ ABC ＝60°，点 E 是射线 CB 上 一点，点 F 是线段 CD 上一点，且∠ EAF ＝120°，求证： AE · CF ＝ AF · BC .
证明：如答图，连接 AC .
∵四边形 ABCD 是菱形，
∴ AB ＝ BC ， AD ∥ BC .
∵∠ ABC ＝60°，
∴△ ABC 是等边三角形.
∴∠ ACB ＝∠ BAC ＝60°， AC ＝ BC .
∵ AD ∥ BC ，∠ ABC ＝60°，
∴∠ BAD ＝120°，∠ CAD ＝∠ ACB ＝∠ ACF ＝60°.
又∵∠ EAF ＝120°，
∴∠ EAB ＝∠ FAD .
设∠ EAB ＝∠ FAD ＝α，则∠ E ＝∠ ABC －α＝60°－α.
∵∠ CAF ＝∠ CAD －∠ FAD ＝60°－α，
∴∠ E ＝∠ CAF .
又∵∠ ACF ＝∠ ACB ＝60°，
∴△ ACF ∽△ ECA .
∵ AC ＝ BC ，
∴ AE · CF ＝ AF · BC .
已知点 E 是矩形 ABCD 的边 BC 上一点，连接 AE ，过点 E 作 EF ⊥ AE 于点 E ，分别交 AC ， CD 于点 M ， F . 过点 B 作 BG ⊥ AC 于点 G ，交 AE 于点 H .
（1）如图1，求证：△ ABE ∽△ ECF ；
（2）如图1，找出与△ ABH 相似的三角形，并证明；
（3）如图2，若点 E 是 BC 的中点， BC ＝2 AB ， AB ＝2，求 EM 的长.
【思路导航】（1）易知∠ ABE ＝∠ ECF ＝90°，要证明△ ABE ∽△ ECF ，只需要再找一组对应角相等即可；（2）找出图中与 ∠ ABH ，∠ BAH 相等的角，进而可找出与△ ABH 相似的三角 形；（3）首先作 MR ⊥ BC ，垂足为 R ，由相似三角形，可求得 MR ， ER 的长，再由勾股定理即可求得 EM 的长.
（1）证明：∵四边形 ABCD 是矩形，∴∠ ABE ＝∠ ECF ＝90°.∵ EF ⊥ AE ，∴∠ AEB ＋∠ FEC ＝90°.又∵∠ AEB ＋∠ BAE ＝90°，∴∠ BAE ＝∠ CEF . ∴△ ABE ∽△ ECF .
（2）解：△ ECM ∽△ ABH . 证明如下：∵ BG ⊥ AC ，∴∠ ABG ＋∠ BAG ＝90°.∵∠ ACB ＋∠ BAC ＝90°，∴∠ ECM ＝∠ ABH . 由（1）知，∠ CEM ＝∠ BAH ，∴△ ECM ∽△ ABH .
（3）解：如图，作 MR ⊥ BC ，垂足为 R .
∵ BC ＝2 AB ，点 E 是 BC 的中点，
∴ BE ＝ EC ＝ AB ＝2.
∴∠ AEB ＝45°.
∴∠ MER ＝45°.
∴ MR ＝ ER .
易知△ MRC ∽△ ABC ，
∴ CR ＝2 MR .
在Rt△ EMR 中，由勾股定理，得
【点拨】注意数形结合思想的应用，以及有两组角对应相等的 两个三角形相似的判定定理的应用.
如图，在平面直角坐标系中，已知点 A ， C 分别在 x 轴和 y 轴 上，四边形 AOCB 为矩形， AB ＝16， BC ＝12，点 D 与点 A 关于 y 轴对称.点 E ， F 分别是线段 AD ， AC 上的动点（点 E 不与点 A ， D 重合），且∠ CEF ＝∠ ACB .
（1）求 AC 的长与点 D 的坐标；
（2）说明△ AEF 与△ DCE 相似；
解：（2）∵点 D 与点 A 关于 y 轴对称，∴∠ CDE ＝∠ CAO . ∵∠ CEF ＝∠ ACB ，∠ ACB ＝∠ CAO ，∴∠ CDE ＝∠ CEF . 又∵∠ AEC ＝∠ AEF ＋∠ CEF ＝∠ CDE ＋∠ DCE ，∴∠ AEF ＝∠ DCE . ∵∠ EAF ＝∠ CDE ，∠ AEF ＝∠ DCE ，∴△ AEF ∽△ DCE .
（3）若△ EFC 为等腰三角形，且 EF ＝ FC ，求点 E 的坐标.