北师数学9年级上册 1.4 回顾与思考 PPT课件

这是一份北师数学9年级上册 1.4 回顾与思考 PPT课件，共27页。

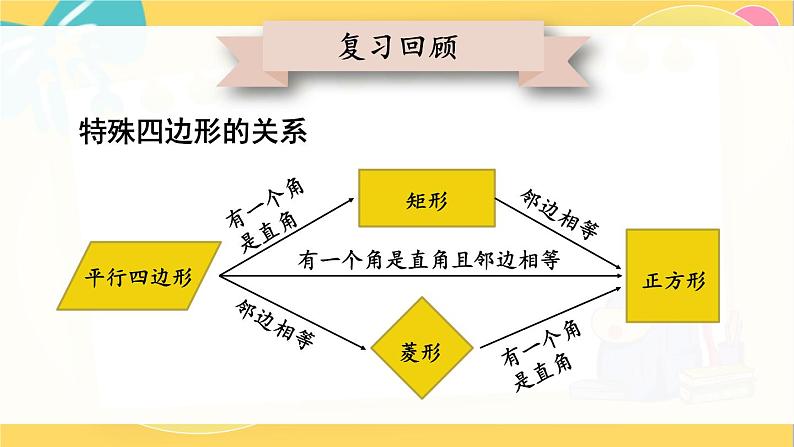
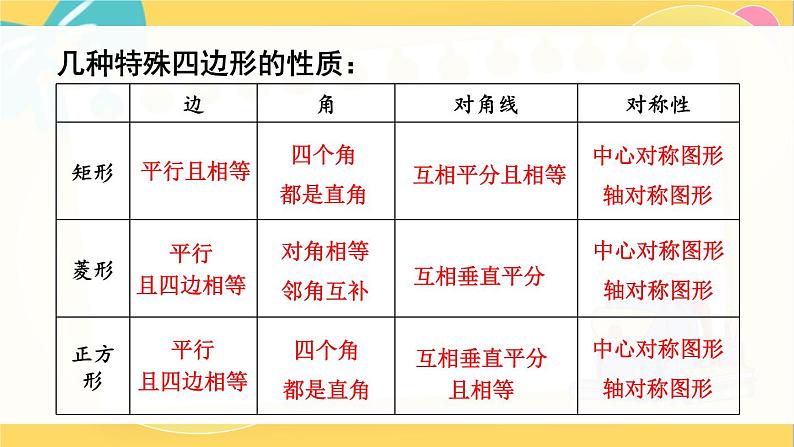
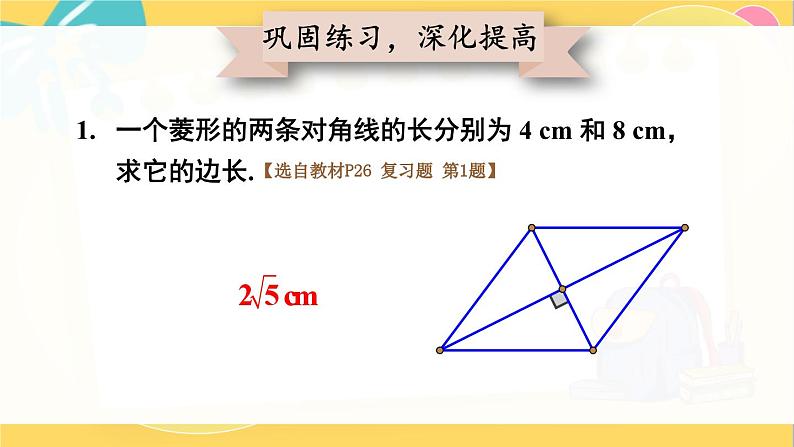
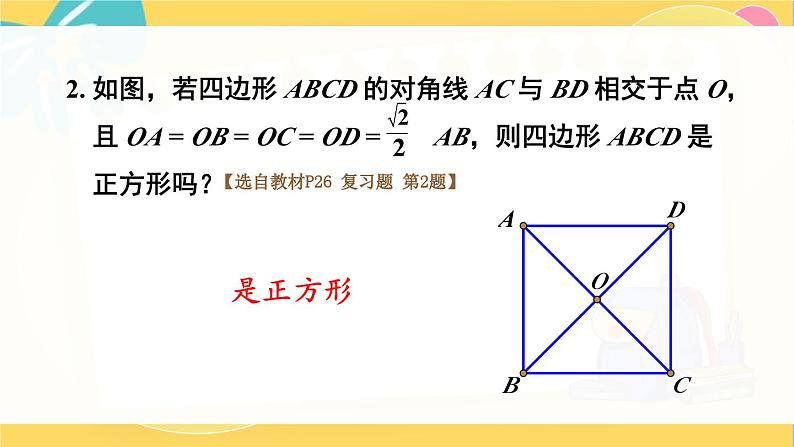
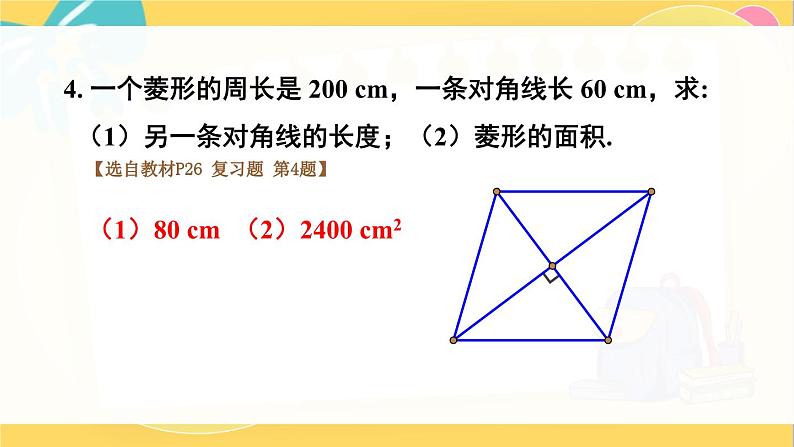
回顾与思考北师版九年级上册复习回顾特殊四边形的关系平行四边形矩形菱形正方形有一个角是直角有一个角是直角且邻边相等邻边相等邻边相等有一个角是直角几种特殊四边形的性质：平行且相等四个角都是直角互相平分且相等中心对称图形轴对称图形平行且四边相等平行且四边相等对角相等邻角互补四个角都是直角互相垂直平分互相垂直平分且相等中心对称图形轴对称图形中心对称图形轴对称图形几种特殊四边形的常用判定方法：1.定义：有一角是直角的平行四边形 2.三个角是直角的四边形3.对角线相等的平行四边形1.定义：一组邻边相等的平行四边形 2.四条边都相等的四边形 3.对角线互相垂直的平行四边形1.定义：一组邻边相等且有一个角是直角的平行四边形2.有一组邻边相等的矩形 3.有一个角是直角的菱形一个菱形的两条对角线的长分别为 4 cm 和 8 cm，求它的边长.【选自教材P26 复习题 第1题】巩固练习，深化提高2. 如图，若四边形 ABCD 的对角线 AC 与 BD 相交于点 О， 且 OA = OB = OC = OD = AB，则四边形 ABCD 是 正方形吗？【选自教材P26 复习题 第2题】是正方形3. 如果一个四边形是轴对称图形，而且有两条互相垂直的 对称轴，那么这个四边形一定是菱形吗？为什么？【选自教材P26 复习题 第3题】不一定，因为筝形也符合条件．4. 一个菱形的周长是 200 cm，一条对角线长 60 cm，求: （1）另一条对角线的长度；（2）菱形的面积.【选自教材P26 复习题 第4题】（1）80 cm （2）2400 cm25. 证明：如果四边形两条对角线互相垂直且相等，那么 以它的四边中点为顶点可组成一个正方形.【选自教材P26 复习题 第5题】证明: 如图， 四边形 ABCD 中，E，F，G，H 分别为 AB，BC，CD ，AD 中点，BD ，AC 交于点 O，则 HE BD FG，HG AC EF．又∵∠COB ＝∠1 ＝ 90°＝∠HEF，∴四边形 EFGH 为正方形．6. 如图，四边形 ABCD 是一个正方形，E 是 BC 延长线上 一点，且 AC = EC，求∠DAE 的度数.【选自教材P26 复习题 第6题】解: 由题意，可知 AC＝ EC，∠CAE＝∠AEC．又∵∠CAE ＋∠AEC ＝ 45°，∴∠CAE ＝ 22.5°，∴∠DAE＝ 22.5.°7.（1）如果一个菱形绕对角线的交点旋转 90°后， 所得图形与原来的图形重合，那么这个菱形是正 方形吗？为什么？解:（1）是正方形．因为绕对角线交点旋转 90°，所得图形与原图形重合，说明菱形两条对角线相等，所以这个菱形是正方形.【选自教材P26 复习题 第7题】7. （2）如果一个四边形绕对角线的交点旋转90°后， 所得图形与原来的图形重合，那么这个四边形是正 方形吗？为什么？【选自教材P26 复习题 第7题】（2）是正方形．因为绕对角线交点旋转 90°，所得图形与原图形重合，说明四个角相等，均为90°，且四条边相等，所以这个四边形是正方形．8. 已知: 如图，AD 是△ABC 的角平分线，过点 D 分别 作 AC 和 AB 的平行线，交 AB 于点 E，交 AC 于点 F . 求证: 四边形 AEDF 是菱形.【选自教材P27 复习题 第8题】证明: ∵AD 为∠BAC 的平分线，∴∠DAC＝∠DAB．又∵DF∥AB，DE∥AC，∴四边形 AEDF 为平行四边形，∠DAC ＝∠EDA ，∠FDA ＝∠EAD ，∴∠FDA ＝∠DAF＝∠EAD ＝∠EDA ,即AF ＝ FD ，AE ＝ ED ．又∵四边形 AEDF 为平行四边形,∴四边形 AEDF 是菱形．9. 已知: △ABC 的两条高分别为 BE，CF，点 M 为 BC 的 中点 . 求证: ME = MF.【选自教材P27 复习题 第9题】证明: 如图．∵△FBC 为直角三角形，△EBC 为直角三角形．M 点为 BC 中点，∴MF＝ BC ＝ EM ．10. 已知正方形的对角线的长为 l，求这个正方形的 周长和面积.【选自教材P27 复习题 第10题】这个正方形的周长为 l；面积为 .11. 已知: 如图，在矩形 ABCD 中，对角线 AC 与 BD 相交 于点 O，过点 C 作 BD 的平行线，过点 D 作 AC 的平 行线，两线相交于点 P. 求证: 四边形 CODP 是菱形.【选自教材P27 复习题 第11题】证明: ∵DP ∥AC，PC∥BD ,∴四边形 OCPD 为平行四边形，OC＝PD ，PC＝OD ．又∵四边形 ABCD 为矩形，∴AC＝BD ，则OC ＝PD ＝ AC ＝ BD ＝ OD ＝ PC．∴四边形 CODP 是菱形．12. 已知: 如图，在矩形 ABCD 中，对角线 AC 与 BD 相交于 点 O，点 M， P，N，Q 分别在 AO，BO，CO，DO 上， 且 AM = BP = CN = DQ. 求证: 四边形 MPNQ 是矩形.【选自教材P27 复习题 第12题】证明: 在矩形 ABCD 中，AM ＝ BP ＝CN ＝ DQ．∴OM ＝ OQ＝ ON ＝ OP ．易证△MOQ≌△PON ．∴MQ ＝ PN ，∠MQP ＝∠NPQ，∴MQ∥PN ，∴四边形 MQNP 为矩形．13. 已知: 如图，在 Rt △ABC 中，∠ACB = 90°， CD 是 △ABC 的角平分线， DE⊥BC，DF⊥ AC，垂足分别为 E，F. 求证: 四边形 CEDF 是正方形.【选自教材P27 复习题 第13题】证明:由题意，知∠FCE＝90°＝∠CED＝∠CFD＝∠FDE．∴四边形 CEDF 为矩形．又∵CD 是△ACB 的角平分线，∴∠DCE＝∠FCD ＝45°＝∠EDC，即DE＝EC，∴四边形 CEDF 是正方形．14. 如图，在矩形 ABCD 中，AB = 20 cm. 动点 P 从点 A 开始沿 AB 边以 4 cm/s 的速度运动，动点 Q 从点 C 开始沿 CD 边以 1 cm/s 的速度运动. 点 P 和点 Q 同时出发，当其中一点到达终点时，另一点也随之停止运动. 设动点的运动时间为 t s，则当 t 为何值时，四边形 APQD 是矩形？【选自教材P27 复习题 第14题】解:根据题意,四边形 APQD 是矩形时，DQ ＝AP ，DQ ＝20－t，AP ＝4t，令 DQ＝AP，即20－t＝4t，解得 t＝4 (s)．∴当 t 为 4 s 时，四边形 APQD 是矩形．几何画板.GSP15. 如图，把一张矩形纸片沿对角线折叠，重合部分 是什么图形？试说明理由.【选自教材P28 复习题 第15题】解: 重合部分是等腰三角形．由题意知，四边形 ABCD 为矩形,∴∠ADB＝∠CBD ＝∠EBD ,即 FB ＝ FD ．故重合部分是等腰三角形．几何画板.GSP16. 如图，把两个全等的矩形 ABCD 和矩形 CEFG 拼成 如图所示的图案，求∠ACF，∠AFC 的度数.【选自教材P28 复习题 第16题】解: 由题意，可得∠FCE＝∠ACD ，∠GCF＝∠BCA ，∴∠ACF＝90°．又∵AC＝CF，∴∠AFC＝45°17. 小颖在商店里看到一块漂亮的方纱巾，非常想买，但当她拿起来时，又感觉纱巾不太方．商店老板看她犹豫的样子，马上过来将纱巾沿对角线对折，让小颖检验（如图）.小颖还是有些疑惑，老板又将纱巾沿另一条对角线对折，让小颖检验，小颖发现这两次对折后两个对角都能对齐，终于下决心买下这块纱巾.你认为小颖买的这块纱巾一定是正方形吗？你认为用什么方法可以检验纱巾是不是正方形？【选自教材P28 复习题 第17题】小颖买的这块纱巾不一定是正方形.18. 已知：如图，平行四边形ABCD 各角的平分线分别相交于点 E，F，G，H 求证：四边形 EFGH 是矩形.【选自教材P28 复习题 第18题】证明: 延长AH ，交 CD 于点 M ，延长BH ，交 CD 于点 N ．由题意，知∠BAM ＝ ∠DAB ＝∠DMA ＝∠DCF，∴EH ∥FG．同理，可证 HG ∥EF，即四边形 EFGH 为平行四边形．又∵ ∠DAB ＋ ∠ABC ＝180°，∴∠HAB＋∠ABH ＝ ×180°＝90°,即∠AHB＝90°，∴四边形 EFGH 为矩形．MN19. 你能通过剪切和拼接下列图形得到一个矩形吗？在这些 剪拼的过程中，剪下的图形是经过怎样的运动最后拼接 在一起的？ 【选自教材P28 复习题 第19题】（1）平行四边形；（2）三角形；（3）菱形几何画板.GSP20. 将相应的条件填在相应的箭头上，使得下图能清楚地 表达几种四边形之间的关系.【选自教材P29 复习题 第20题】四边形平行四边形矩形菱形正方形两组对边分别平行的四边形有一个角是直角的平行四边形有一组邻边相等的平行四边形有一组邻边相等的矩形有一个角是直角的菱形21. 已知两条对角线，利用尺规作一个菱形.【选自教材P29 复习题 第21题】课堂小结这节课你们都学会了哪些知识？状元成才路