青岛版初中八年级数学上册第2章素养基础测试卷课件

这是一份青岛版初中八年级数学上册第2章素养基础测试卷课件，共34页。

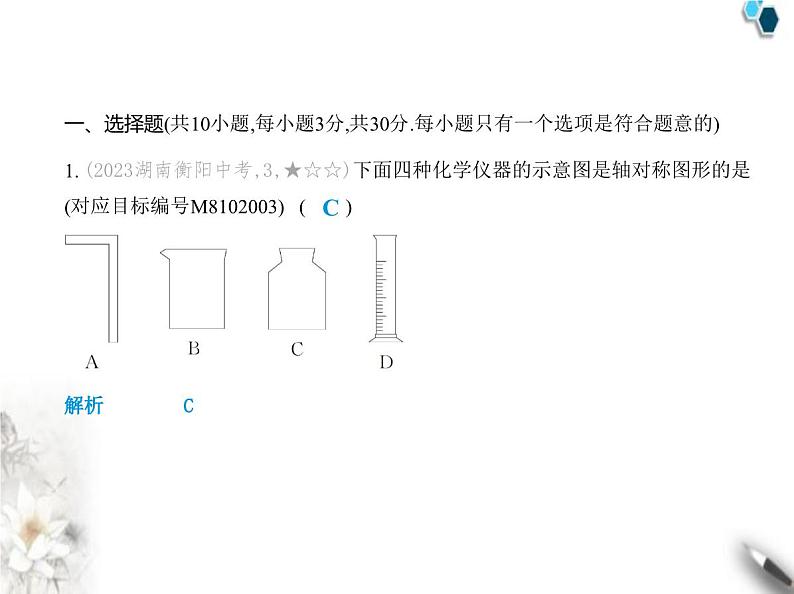
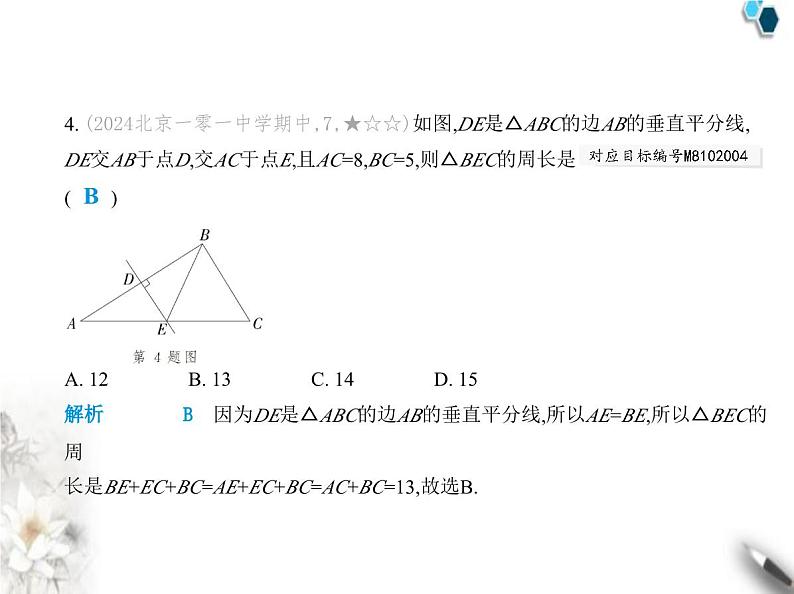
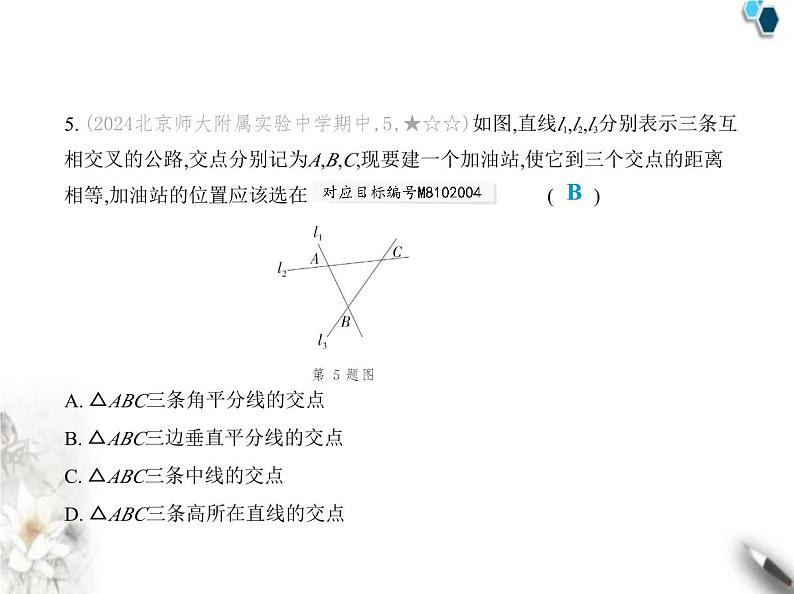
(时间：90分钟 满分：120分)第2章　素养基础测试卷一、选择题(共10小题,每小题3分,共30分.每小题只有一个选项是符合题意的)1. (2023湖南衡阳中考,3,★☆☆)下面四种化学仪器的示意图是轴对称图形的是(对应目标编号M8102003) (　    ) 　     　     　      C解析    C    2. (2023湖南怀化中考,5,★☆☆)在平面直角坐标系中,点P(2,-3)关于x轴对称的点P'的坐标是 (　    )A. (-2,-3)　　　    B. (-2,3)　　　    C. (2,-3)　　　    D. (2,3)D解析    D　根据关于x轴对称的点的坐标特点:横坐标不变,纵坐标互为相反数,可知点P(2,-3)关于x轴对称的点P'的坐标是(2,3),故选D.3. (2023江苏宿迁中考,5,★☆☆)若等腰三角形有一个内角为110°,则这个等腰三角形的底角是(对应目标编号M8102007) (　    )A. 70°　　　    B. 45°　　　    C. 35°　　　    D. 50°C4. (2024北京一零一中学期中,7,★☆☆)如图,DE是△ABC的边AB的垂直平分线,DE交AB于点D,交AC于点E,且AC=8,BC=5,则△BEC的周长是(　    ) A. 12　　　    B. 13　　　    C. 14　　　    D. 15B解析    B　因为DE是△ABC的边AB的垂直平分线,所以AE=BE,所以△BEC的周长是BE+EC+BC=AE+EC+BC=AC+BC=13,故选B.5. (2024北京师大附属实验中学期中,5,★☆☆)如图,直线l1,l2,l3分别表示三条互相交叉的公路,交点分别记为A,B,C,现要建一个加油站,使它到三个交点的距离相等,加油站的位置应该选在 (　    ) A. △ABC三条角平分线的交点B. △ABC三边垂直平分线的交点C. △ABC三条中线的交点D. △ABC三条高所在直线的交点B解析    B　到点A,B距离相等的点在线段AB的垂直平分线上,到A、C距离相等的点在线段AC的垂直平分线上,到点B,C距离相等的点在线段BC的垂直平分线上.因为加油站到点A,B,C的距离相等,所以加油站为AB、BC、AC的垂直平分线的交点,故选B.6. (2024山东聊城阳谷期末,5,★☆☆)如图,将长方形纸片ABCD沿对角线BD折叠,点C的对应点为E,若∠CBD=35°,则∠AFB的度数为 (　    ) A. 70°　　　    B. 75°　　　    C. 80°　　　    D. 85°A解析    A　由折叠的性质,得∠EBD=∠CBD=35°,所以∠EBC=∠EBD+∠CBD=70°.因为四边形ABCD是长方形,所以AD∥BC,所以∠AFB=∠EBC=70°,故选A.7. (2024山东菏泽成武期中,4,★☆☆)如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD  (　    ) A. 36°　　　    B. 54°　　　    C. 18°　　　    D. 64°B解析    B　在等腰△ABC中,AB=AC,∠ABC=72°,所以∠ABC=∠ACB=72°,所以∠A=180°-∠ABC-∠ACB=36°.因为BD⊥AC,所以∠ADB=90°,所以∠ABD=180°-∠ADB-∠A=54°.故选B.8. (2024山东滨州滨城期中,4,★★☆)下列推理中,不能判断△ABC是等边三角形的是 (　    )A. ∠A=∠B=∠C　　　     B. AB=AC,∠B=60°C. ∠A=60°,∠B=60°　　　    D. AB=AC,且∠B=∠CD解析    D　选项A,由“三个角都相等的三角形是等边三角形”可以判断△ABC是等边三角形,选项A不符合题意.选项B,由“有一个角是60°的等腰三角形是等边三角形”可以判断△ABC是等边三角形,选项B不符合题意.选项C,由“∠A=60°,∠B=60°”可以得到“∠A=∠B=∠C=60°”,由“三个角都相等的三角形是等边三角形”可以判断△ABC是等边三角形,选项C不符合题意.由“AB=AC,且∠B=∠C”只能判定△ABC是等腰三角形,不可以判断△ABC是等边三角形,选项D符合题意.故选D.9. (2024山东菏泽成武期末,3,★★☆)如图,在△ABC中,AB=AC,AD是△ABC的角平分线,过点D分别作DE⊥AB,DF⊥AC,垂足分别是点E,F,则下列结论不一定正确的是(　    ) A. ∠ADC=90°　　　    B. DE=DFC. AD=BC　　　     D. BD=CDC解析    C　因为AB=AC,AD是△ABC的角平分线,所以AD⊥BC,BD=CD,∠B=∠C,所以∠ADC=90°.因为AD平分∠BAC,DE⊥AB,DF⊥AC,所以DE=DF.根据题中条件,无法证明AD=BC,故选项C符合题意,故选C.10. (2024山东聊城冠县期中,12,★★☆)如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上的一动点.若AB=5,AC=4,BC=6,则△APC周长的最小值是 (        ) A. 9　　　    B. 10　　　    C. 10.5　　　    D. 11A解析    A　连接BP(图略),因为直线m是△ABC中BC边的垂直平分线,所以BP=PC,所以△APC的周长=AC+AP+PC=AC+AP+BP.因为两点之间线段最短,所以AP+BP≥AB,所以△APC的周长=AC+AP+BP≥AC+AB,因为AC=4,AB=5,所以△APC周长的最小值为AC+AB=9,故选A.二、填空题(共6个小题,每小题4分,共24分)11. (2024山东泰安宁阳期末,13,★☆☆)如图,△ABC和△A'B'C'关于直线l对称.若∠A=45°,∠C'=30°,则∠B的度数为　　　    .  105°答案    105°解析　因为△ABC和△A'B'C'关于直线l对称,所以△ABC≌△A'B'C',所以∠C=∠C'=30°,所以∠B=180°-∠A-∠C=180°-45°-30°=105°.12. (2024北京朝阳陈经纶中学分校期中,15,★☆☆)如图,在△ABC中,∠C=90°,AD是∠CAB的平分线,已知AC=4 cm,AB=5 cm,则S△ACD∶S△ABD=　　　    .  4∶5答案    4∶5解析　如图,过D作DE⊥AB于E,因为AD是∠CAB的平分线,∠C=90°,所以DE=DC.因为S△ACD= AC·DC,S△ABD= AB·DE,所以S△ACD∶S△ABD=AC∶AB=4∶5.13. (★☆☆)如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC,若∠AEB=50°,则∠EBC的度数是　　　    .   25°14. (新考向　尺规作图)(2023吉林中考,11,★★☆)如图,在△ABC中,AB=AC.分别以点B和点C为圆心,大于 BC的长为半径作弧,两弧交于点D,作直线AD交BC于点E.若∠BAC=110°,则∠BAE的大小为　　　    度.  55答案    55解析　因为AB=AC,所以△ABC是等腰三角形,所以点A在BC的垂直平分线上.因为分别以点B和点C为圆心,大于 BC的长为半径作弧,两弧交于点D,所以DB=DC,所以点D在BC的垂直平分线上,所以AE垂直平分BC,所以AE⊥BC,因为AB=AC,所以AE是∠BAC的平分线,所以∠BAE= ∠BAC=55°.15. (2024山东菏泽曹县期末,17,★★☆)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=　　　    °.  35答案    35解析　如图,过点M作MN⊥AD于N.因为∠B=∠C=90°,所以∠B+∠C=180°,所以AB∥CD,所以∠DAB=180°-∠ADC=70°.因为DM平分∠ADC,MN⊥AD,MC⊥CD,所以MN=MC,因为M是BC的中点,所以MC=MB,所以MN=MB,又MN⊥AD,MB⊥AB,所以AM平分∠DAB,所以∠MAB= ∠DAB=35°.  16. (2023山东威海中考,14,★★☆)如图,在正方形ABCD中,分别以点A,B为圆心,以AB的长为半径画弧,两弧交于点E,连接DE,则∠CDE=　　　    °.  15答案    15解析　如图,连接AE、BE,由题意,得AE=BE=AB,所以△ABE是等边三角形,所以∠EAB=60°.在正方形ABCD中,AB=AD,∠ADC=∠DAB=90°,所以AE=AD,∠DAE=∠DAB-∠EAB=30°,所以∠ADE=∠AED= ×(180°-30°)=75°,所以∠CDE=∠ADC-∠ADE=15°.  三、解答题(共6个题,共66分)17. (2024山东菏泽曹县期中,21,★☆☆)(10分)已知△ABC,点A,B,C的坐标分别为A(3,0),B(-2,3),C(-4,-2),在如图所示的直角坐标系中,画出△ABC和它关于x轴对称的△A'B'C',并写出点A',B',C'的坐标.  解析　如图,△ABC即为所求.点A(3,0)关于x轴对称的点的坐标为A'(3,0),点B(-2,3)关于x轴对称的点的坐标为B'(-2,-3),点C(-4,-2)关于x轴对称的点的坐标为C'(-4,2),如图所示,△A'B'C'即为所求.  18. (学科素养　应用意识)(★★☆)(10分)如图,计划在某小区建一个智能垃圾分类投放点P,需要满足以下条件:附近的两栋住宅楼A,B到智能垃圾分类投放点P的距离相等,P点到两条道路OM,ON的距离相等.请在图中利用尺规作图(保留作图痕迹,不写作法),确定点P的位置.  解析　如图,点P即为所求.  19. (2024山东聊城阳谷期中,20,★★☆)(10分)如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是9 cm2,AB=5 cm,AC=4 cm,求DE的长.  解析　因为AD为∠BAC的平分线,DE⊥AB,DF⊥AC,所以DE=DF.因为S△ABC=S△ABD+S△ACD= AB·DE+ AC·DF= (AB+AC)·DE,△ABC的面积是9 cm2,所以 ×(5+4)×DE=9,所以DE=2 cm.20. (2024山东菏泽定陶期末,20,★★☆)(10分)如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,点D为CE的中点,连接AD,此时∠CAD=24°,∠ACB=66°.求证:BE=AC.  证明　如图,连接AE.在△ADC中,因为∠ACB=66°,∠DAC=24°,所以∠ADC=180°-∠DAC-∠ACB=180°-24°-66°=90°,所以AD⊥EC.因为点D为CE的中点,所以DE=DC,所以AD是线段CE的垂直平分线,所以AE=AC.因为EF垂直平分AB,所以AE=BE,所以BE=AC.  21. [教材变式P59挑战自我](2024山东潍坊诸城期中,20,★★☆)(12分)如图,在△ABC中,BO和CO分别平分∠ABC和∠ACB,BO和CO交于点O,过O作MN∥BC,分别交AB,AC于点M,N.(1)指出图中的等腰三角形,并说明理由.(2)若AB=7,AC=5,求△AMN的周长.  解析    (1)图中的等腰三角形有△MOB,△NOC.理由:因为BO和CO分别平分∠ABC和∠ACB,所以∠ABO=∠OBC,∠ACO=∠OCB,因为MN∥BC,所以∠MOB=∠OBC,∠NOC=∠OCB,所以∠ABO=∠MOB,∠ACO=∠NOC,所以MB=MO,NO=NC,所以△MOB和△NOC都是等腰三角形.(2)因为AB=7,AC=5,MB=MO,NO=NC,所以△AMN的周长=AM+MN+AN=AM+MO+ON+AN=AM+MB+NC+AN=AB+AC=7+5=12,即△AMN的周长是12.22. (学科素养　推理能力)(2023山东菏泽曹县期中,27,★★☆)(14分)如图,P为等边△ABC的边BC延长线上一点,BP=CD,∠DCP=60°.(1)说明△ABP≌△ACD的理由.(2)判断△ADP是什么特殊三角形,并说明理由.  解析    (1)因为△ABC是等边三角形,所以AB=AC=BC,∠ABC=∠ACB=∠BAC=60°,因为∠DCP=60°,所以∠ACD=180°-∠ACB-∠DCP=60°,所以∠B=∠ACD.因为AB=AC,BP=CD,所以△ABP≌△ACD(SAS).(2)△ADP是等边三角形.理由如下:因为△ABP≌△ACD,所以AP=AD,∠BAP=∠CAD,所以∠BAP-∠CAP=∠CAD-∠CAP,即∠BAC=∠PAD,因为∠BAC=60°,所以∠PAD=60°,又因为AP=AD,所以△ADP是等边三角形.