
2023-2024学年河南省郑州市郑州东区七年级(下)期末数学试卷(含解析)
展开1.第33届夏季奥林匹克运动会将于2024年7月26日在巴黎开幕,此次奥运会体育项目图标充满了图形变换的元素.下列运动项目图标中,不是轴对称图形的是( )
A. B. C. D.
2.若∠1和∠2互补,∠1=36°,则∠2的度数是( )
A. 44°B. 54°C. 144°D. 154°
3.下列计算正确的是( )
A. x5+x5=x10B. b6÷b3=b2C. (ab4)4=a4b16D. (−c2)2n=−c4n
4.如图所示,货车匀速通过隧道(隧道长大于货车长)时,货车从进入隧道至离开隧道的时间x与货车在隧道内的长度y之间的关系用图象描述大致是( )
A. B.
C. D.
5.小红在学习垂线时遇到了这样一个问题,请你帮她解决:如图,线段AB和CD相交于点O,则下列条件中能说明AB⊥CD的是( )
A. AO=OB
B. CO=OD
C. ∠AOC=∠BOD
D. ∠AOC=∠BOC
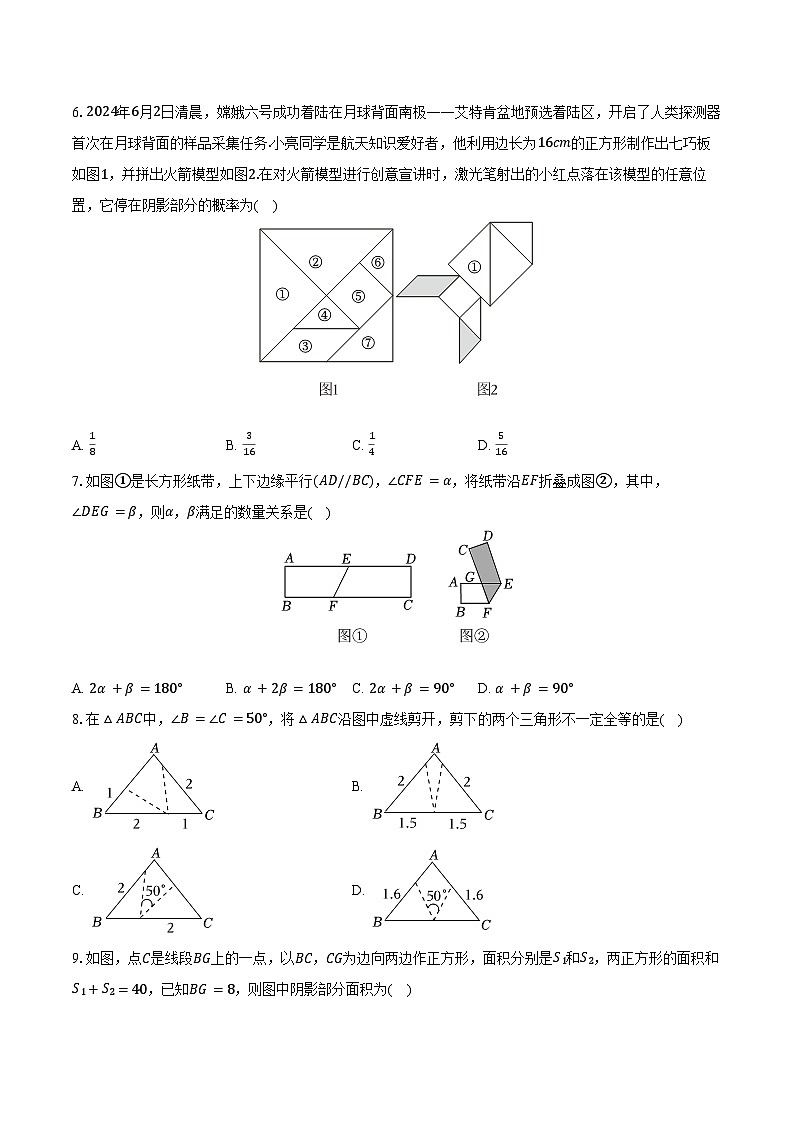
6.2024年6月2日清晨,嫦娥六号成功着陆在月球背面南极——艾特肯盆地预选着陆区,开启了人类探测器首次在月球背面的样品采集任务.小亮同学是航天知识爱好者,他利用边长为16cm的正方形制作出七巧板如图1,并拼出火箭模型如图2.在对火箭模型进行创意宣讲时,激光笔射出的小红点落在该模型的任意位置,它停在阴影部分的概率为( )
A. 18B. 316C. 14D. 516
7.如图①是长方形纸带,上下边缘平行(AD//BC),∠CFE=α,将纸带沿EF折叠成图②,其中,∠DEG=β,则α,β满足的数量关系是( )
A. 2α+β=180°B. α+2β=180°C. 2α+β=90°D. α+β=90°
8.在△ABC中,∠B=∠C=50°,将△ABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
A. B.
C. D.
9.如图,点C是线段BG上的一点,以BC,CG为边向两边作正方形,面积分别是S1和S2,两正方形的面积和S1+S2=40,已知BG=8,则图中阴影部分面积为( )
A. 6
B. 8
C. 10
D. 12
10.如图,在四边形ACDB中,∠CAB=114°,M、N分别是BD、CD上的点,当△AMN的周长最小时,则∠MAN的度数为( )
A. 66°
B. 48°
C. 57°
D. 90°
二、填空题:本题共5小题,每小题3分,共15分。
11.自2004年探月一期工程正式立项起,20年来中国探月工程八战八捷,每一步都取得了重要成果.已知月球的半径长约为1.7×103km,地球的半径大概是月球的3.7倍,则地球半径约为______km.
12.如图,B是AD中点,∠C=∠E,请添加一个条件,使得△ABC≌△DBE,可以添加的条件是______.(写出一个即可)
13.如图,某种型号的自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.如果x节链条的总长度是ycm,那么y与x之间的关系式为______.
14.如图,D是△ABC内一点,且AD平分∠BAC,CD⊥AD连接BD,若△ABD的面积为16,那么△ABC的面积是______.
15.如图,在△ABC中,AB=AC,∠ABC=75°,分别以A,B为圆心,以AB长为半径的两条弧相交于点P,则∠APC的度数为______.
三、解答题:本题共7小题,共55分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题9分)
(1)计算:(12)0+5−2−(−1)2024.
(2)先化简,再求值:[(2x−y)(2x+y)−(x−y)2−3x2]÷2y,其中x=1,y=2.
17.(本小题6分)
为了方便市民绿色出行和锻炼身体,环保人士倡导大家使用共享单车.图1是一辆共享单车放在水平地面上的实物图,图2是其示意图,其中AB//l,CD//l,∠BCD=72°,∠BAC=50°.若AM//BC,求∠MAC的度数.
18.(本小题7分)
如图,在8×8的网格中,每个小正方形的边长都为1,△ABC的顶点都在格点上,仅用无刻度的直尺在给定的网格中分别按下列要求画图(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示).
(1)画出△ABC关于AC对称的△ACD(点B的对应点是点D).
(2)画出△ABC的重心O.
(3)直接写出四边形ABCD的面积______.
19.(本小题7分)
在一个不透明的盒子里装有红、黑两种颜色的球共60只,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,七(1)班的数学学习小组做了摸球试验.他们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到表中的一组统计数据:
(1)补全表格中的数据:a= ______,b= ______.
(2)请估计:当次数n足够大时,摸到红球频率将会接近______.(精确到0.1)
(3)小明、小亮做游戏,游戏规则是:从盒子中任意摸出一个球,摸到红球小明胜,摸到黑球小亮胜.你认为这个游戏公平吗?若公平,说明理由:若不公平,怎样调整,使得游戏公平.
20.(本小题7分)
学习《利用三角形全等测距离》后,数学兴趣小组同学就“测量河两岸A、B两点间距离”这一问题,设计了如下方案.
(1)A、B两点间距离是______米.
(2)请你说明方案正确的理由.
21.(本小题7分)
研究表明,当每公顷土地中钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
如果用x表示氮肥施用量,用y表示土豆产量,根据表中的实验数据,将氮肥施用量x与土豆产量y的关系拟合成图象,见图:
(1)上述问题中的两个变量,自变量是______.
(2)图中点A表示的实际意义是______.
(3)当每公顷土地氮肥的施用量为100kg时,土豆的产量约为______kg.(保留两位小数)
(4)你认为氮肥的施用量大概是多少时比较适宜?说说你的理由.
22.(本小题12分)
劳动课上,老师给同学们布置了任务:将手边的三角形边角料加工成等腰三角形样式的部件.为了合理利用、科学剪裁,同学们开启了探究活动.
【测量】
如图,是一块三角形板材,经过测量发现,△ABC中,∠BAC=4∠ACB.
【操作】
(1)利用无刻度的直尺和圆规,作∠BAC的平分线AD,交BC于点E.(保留画图痕迹,不写作法)
【探究】
(2)在第(1)题完成的图形中,若△ABE是等腰三角形,则∠ACB是多少度.
【挑战】
(3)在第(1)题完成的图形中,请你试着把△ACE分成两个等腰三角形,并说明分法的合理性.
答案解析
1.B
【解析】解:A.图形是轴对称图形,不符合题意;
B.图形不是轴对称图形,符合题意;
C.图形是轴对称图形,不符合题意;
D.图形是轴对称图形,不符合题意,
故选:B.
根据轴对称图形的定义:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形进行逐一判断即可.
本题主要考查了轴对称图形和中心对称图形的识别,熟练掌握相关定义是解答本题关键.
2.C
【解析】解:∵∠1和∠2互补,∠1=36°,
∴∠2=180°−36°=144°,
故选:C.
若两个角的和为180°,则这两个角互为补角,据此即可求得答案.
本题考查余角和补角,熟练掌握其定义是解题的关键.
3.C
【解析】解:A、x5+x5=2x5,故该项不正确,不符合题意;
B、b6÷b3=b3,故该项不正确,不符合题意;
C、(ab4)4=a4b16,故该项正确,符合题意;
D、(−c2)2n=c4n,故该项不正确,不符合题意;
故选:C.
根据同底数幂的除法法则、合并同类项的方法、幂的乘方与积的乘方法则进行解题即可.
本题考查同底数幂的除法、合并同类项、幂的乘方与积的乘方,熟练掌握运算法则是解题的关键.
4.A
【解析】解:根据题意可知货车进入隧道的时间x与货车在隧道内的长度y之间的关系具体可描述为:
当货车开始进入隧道时y逐渐变大,当货车完全进入隧道,由于隧道长大于货车长,此时y不变且最大,
当货车开始离开隧道时y逐渐变小.另外货车是匀速运动,货车进入隧道或离开隧道y随x的均匀变化而均匀增大或减小,故图象呈直线型,排除选项B、C、D.
故选:A.
根据当货车开始进入隧道时y均匀变大,当货车完全进入隧道,y值不变且等于车长,当货车开始离开隧道时y均匀变小,逐一判断.
本题主要考查了一次函数的应用,解决问题的关键是熟练掌握函数值随自变量变化的增减性质和均匀性.
5.D
【解析】【分析】
本题考查垂直的概念,以及线段中点和对顶角的定义,掌握相关概念是解题关键.根据线段的中点,对顶角以及垂直的定义分析即可.
【解答】
解:A.由OA=OB只能得出O是AB的中点,故A选项不符合题意;
B.由OC=OD只能得出O是CD的中点,故B选项不符合题意;
C.∠AOC和∠BOD是对顶角,始终是相等的,故C选项不符合题意;
D.∠AOC和∠BOC互补,当∠AOC=∠BOC时,∠AOC=180°÷2=90°,
∴CD⊥AB,故选项D符合题意;
故选D.
6.B
【解析】解:因为边长为16cm的正方形可分成16个图④的等腰直角三角形,图③可分割成2个图④的等腰直角三角形,
所以激光笔射出的小红点落在该模型的任意位置,它停在阴影部分的概率=316.
故选:B.
利用正方形的性质得到大正方形可分成16个图④的等腰直角三角形,图③可分割成2个图④的等腰直角三角形,然后根据几何概率的计算方法求解.
本题考查了几何概率:某事件的概率=某事件所占有的面积与总面积之比.
7.A
【解析】解:如图②,
由折叠的性质得到:∠EFG=∠EFK=α,
∵AE//BF,
∴∠FEG=∠EFK=α,
∴∠CGE=∠EFG+∠FEG=2α,
∵CG//DE,
∴∠CGE+∠DEG=180°,
∴2α+β=180°.
故选:A.
由折叠的性质得到∠EFG=∠EFK=α,由平行线的性质推出∠FEG=∠EFK=α,∠CGE+∠DEG=180°,由三角形外角的性质得到∠CGE=∠EFG+∠FEG=2α,于是得到2α+β=180°.
本题考查平行线的性质,折叠的性质,三角形外角的性质,关键是由折叠的性质得到∠EFG=∠EFK,由三角形外角的性质求出∠CGE,由平行线的性质推出∠FEG=∠EFK=α,∠CGE+∠DEG=180°.
8.D
【解析】解:A、根据SAS可以推出剪下的两个三角形全等,故A选项不符合题意;
B、根据SAS可以推出剪下的两个三角形全等,故B选项不符合题意;
C、如下图:
∵∠DFC=∠DFE+∠EFC且∠DFC=∠B+∠BDF,
∴∠DFE+∠EFC=∠B+∠BDF,
∵∠B=∠DFE=50°,
∴∠EFC=∠BDF,
∵BD=FC,∠B=∠C,
∴△DBF≌△FCE(ASA).
根据ASA可以推出剪下的两个三角形全等,故C选项不符合题意;
D、如下图:
由C选项可得:∠EFC=∠BDF,∠B=∠C,但FC不一定等于BD,,所以两个三角形不一定全等,故D选项符合题意;
故选:D.
根据全等三角形的判定定理逐个判断即可.
本题考查了全等三角形的判定,掌握三角形全等的判定方法是解题的关键.
9.A
【解析】【分析】
本题考查完全平方公式的运用,正方形、三角形面积公式,通过面积关系构造使用完全平方公式的条件是求解本题的关键.
设BC=a,CG=b,建立关于a,b的关系,最后求阴影部分面积.
【解答】
解:设BC=a,CG=b,则S1=a2,S2=b2,a+b=BG=8.
∴a2+b2=40.
∵(a+b)2=a2+b2+2ab=64,
∴2ab=64−40=24,
∴ab=12,
∴阴影部分的面积等于12ab=12×12=6.
故选:A.
10.B
【解析】解:作A关于BD和CD的对称点A′,A″,连接A′A″,交BD于M,交CD于N,则A′A″即为△AMN的周长最小值.作CA延长线AH,
∵∠CAB=114°,
∴∠HAA′=66°,
∴∠AA′M+∠A″=∠HAA′=66°,
∵∠MA′A=∠MAA′,∠NAC=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAC+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAC+∠A″=2(∠AA′M+∠A″)=2×66°=132°,
∴∠MAN=48°,
故选:B.
根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BD和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=66°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
本题考查的是轴对称−最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出E,F的位置是解题关键.
×103
【解析】解:地球半径约为:3.7×1.7×103km=6.29×103km.
故答案为:6.29×103.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
12.∠A=∠D(答案不唯一)
【解析】解:∵AB=DB,∠CBE=∠ABD,
∴可添加∠A=∠D,
在△ABC和△DBE中,
∠C=∠E∠A=∠DAB=DB,
∴△ABC≌△DBE(SAS),
故答案为:∠A=∠D答案不唯一).
由条件AB=DB,∠C=∠E,故可再添加一组角相等.
本题主要考查全等三角形的判定,掌握全等三角形的判定方法SSS、SAS、ASA、AAS和HL是解题的关键.
13.y=1.7x+0.8
【解析】解:2.5−0.8=1.7(cm),
∵1节链条的长度为:2.5,
2节链条的长度为:2.5+1.7,
3节链条的长度为:2.5+1.7×(3−1),
∴y=2.5+1.7(x−1)
=1.7x+0.8.
故答案为:y=1.7x+0.8.
通过列举法,找出规律,归纳出x节链条的总长度即可.
本题考查了函数关系式,掌握通过列举得到:x节链条的总长度=2.5+1.7(x−1)是解题的关键.
14.32
【解析】解:延长CD交AB于E,如下图所示:
∵AD平分∠BAC,
∴∠CAD=∠EAD,
∵CD⊥AD,
∴∠ADC=∠ADE=90°,
在△ADC和△ADE中
∠CAD=∠EAD,AD=AD,∠ADC=∠ADE=90°,
∴△ADC≌△ADE(ASA),
∴CD=DE,S△ADC=S△ADE,
∴S△BCD=S△BDE,
∴S△ADC+S△BCD=S△ADE+S△BDE=S△ABD,
∴S△ABC=2S△ABD=32.
故答案为:32.
延长CD交AB于E,证明△ADC和△ADE全等得CD=DE,S△ADC=S△ADE,进而得S△BCD=S△BDE,由此得S△ADC+S△BCD=S△ABD,则S△ABC=2S△ABD,据此可得△ABC的面积.
此题主要考查了角平分线的定义,全等三角形的判定和性质,理解角平分线的定义,熟练掌握全等三角形的判定和性质是解决问题的关键.
15.45°或75°
【解析】解:分两种情况讨论如下:
①当交点P在AB的左侧时,连接PB,如图1所示:
由作图可知:AP=AB=PB,
∴△ABP为等边三角形,
∴∠PAB=60°,
∵AB=AC,∠ABC=75°,
∴∠ACB=∠ABC=75°,AP=AB=AC,
∴∠BAC=180°−(∠ACB+∠ABC)=30°,
∴∠PAC=∠PAB+∠BAC=60°+30°=90°,
∴△APC为等腰直角三角形,
∴∠APC=45°;
②当交点P在AB的右侧时,连接PB,如图2所示:
同理:△ABP为等边三角形,∠BAC=30°,AP=AC,
∴∠PAB=60°,
∴∠CAP=∠PAB−∠BAC=30°,
∴∠APC=∠ACP=12(180°−∠CAP)=12×(180°−30°)=75°.
综上所述:∠APC的度数为45°或75°.
故答案为:45°或75°.
分两种情况讨论如下:①当交点P在AB的左侧时,连接PB,由作图可知△ABP为等边三角形,则∠PAB=60°,根据AB=AC,∠ABC=75°得∠BAC=30°,则∠PAC=∠PAB+∠BAC=90°,由此得△APC为等腰直角三角形,进而可得∠APC的度数;②当交点P在AB的右侧时,连接PB,同理△ABP为等边三角形,∠BAC=30°,AP=AC,则∠PAB=60°,进而得∠CAP=∠PAB−∠BAC=30°,由此可得∠APC的度数,综上所述即可得出答案.
此题主要考查了等腰三角形的性质,准确识图,熟练掌握等腰三角形的性质是解决问题的关键.
16.解:(1)(12)0+5−2−(−1)2024
=1+125−1
=125;
(2)[(2x−y)(2x+y)−(x−y)2−3x2]÷2y
=(4x2−y2−x2+2xy−y2−3x2)÷2y
=(2xy−2y2)÷2y
=x−y,
当x=1,y=2时,原式=1−2=−1.
【解析】(1)先化简各式,然后再进行计算即可解答;
(2)先利用完全平方公式,平方差公式计算括号里,再算括号外,然后把x,y的值代入化简后的式子进行计算,即可解答.
本题考查了整式的混合运算−化简求值,完全平方公式,平方差公式,实数的运算,准确熟练地进行计算是解题的关键.
17.解:∵AB//CD,
∴∠BAC+∠ACD=180°即∠BAC+∠ACB+∠BCD=180°
∵∠BCD=72°,∠BAC=50°
∴∠ACB=58°,
∵AM//BC,
∴∠AMC=∠ACB=58°.
【解析】根据平行线的判定定理与性质定理求解即可.
此题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.
18.24
【解析】解:(1)如图,△ACD即为所求;
(2)如图,点O即为所求;
(3)四边形ABCD的面积=2×12×4×6=24.
故答案为:24.
(1)利用轴对称变换的性质作出图形即可;
(2)作出中线BF,AE交于点O,点O即为所求;
(3)根据四边形ABCD的面积=△ABC的面积的2倍求解.
本题考查作图−轴对称变换,三角形的重心等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
19.33 0.301 0.3
【解析】解:(1)a=100×0.33=33,b=602÷2000=0.301;
故答案为:33,0.301;
(2)当次数n足够大时,摸到红球的频率将会接近0.3,
故答案为:0.3;
(3)∵摸到红球的概率小于摸到黑球的概率,
∴这个游戏不公平.
方法:盒子里装有红、黑两种颜色的球各20只;
游戏规则是:从盒子中任意摸出一个球,摸到红球小明胜,摸到黑球小亮胜.
(1)根据频数、频率与总数之间的关系即可得出a和b;
(2)由表中摸球次数逐渐增大后,摸到红球的频率逐渐靠近于0.3可得;
(3)根据摸到红球的概率判断即可.
此题考查了利用频率估计概率.大量反复试验下频率稳定值即概率.用到的知识点为:部分的具体数目=总体数目×相应频率.
20.30
【解析】解:(1)∵∠DCB=100°,∠ADC=65°,
∴∠A=180°−∠DCB−∠ADC=15°,
∵∠E=15°,
∴∠A=∠E,
在△DCA和△BCE中,
∠A=∠E∠ACD=∠ECBCD=BC,
∴△DCA≌△BCE(AAS),
∴AC=EC,
∵BC=CD,
∴AC−BC=CE−CD,即AB=DE,
∴测得DE的长就是A、B两点间的距离,即30米,
故答案为:30;
(2)理由:∵∠DCB=100°,∠ADC=65°,
∴∠A=180°−∠DCB−∠ADC=15°,
∵∠E=15°,
∴∠A=∠E,
在△DCA和△BCE中,
∠A=∠E∠ACD=∠ECBCD=BC,
∴△DCA≌△BCE(AAS),
∴AC=EC,
∵BC=CD,
∴AC−BC=CE−CD,即AB=DE,
∴测得DE的长就是A、B两点间的距离.
证明△DCA≌△BCE(AAS),推出AC=EC,即可得到结论.
本题考查了全等三角形的判定和性质,熟练掌握知识点是解题的关键.
21.氮肥施用量 不施用氮肥时,每公顷土地土豆的产量约为15tkg 21t
【解析】解:(1)上述问题中的两个变量,自变量是氮肥施用量;
故答案为:氮肥施用量;
(2)图中点A表示的实际意义是不施用氮肥时,每公顷土地土豆的产量约为15tkg;
故答案为:不施用氮肥时,每公顷土地土豆的产量约为15tkg;
(3)当每公顷土地氮肥的施用量为100kg时,土豆的产量约为2tkg,
故答案为:21t;
(4)由图象可知,氮肥的施用量大概是300kg时比较适宜,因为此时每公顷土地土豆的产量最高.
(1)根据函数的定义解答即可;
(2)根据图象解答即可;
(3)观察图象可得当每公顷土地氮肥的施用量为100kg时,土豆的产量约为21tkg;
(4)观察图象的最高点可得答案.
本题考查函数的图象,利用数形结合的思想解答是解答本题的关键.
22.解:(1)图形如图所示:
(2)当∠B=∠BAE时,设∠ACB=x,则有x+4x+2x=180°,
∴x=(1807)°.
当B=∠AEB时,设∠ACB=y,则有y+4y+3y=180°,
y=22.5°.
综上所述,∠ACB的度数为(1807)°或22.5°;
(3)如图点F即为所求.
理由:∵EA=EF,
∴∠EAF=∠EFA,
∵∠EAF=∠BAE=2∠C,∠AFE=∠C+∠FEC,
∴∠C=∠FEC,
∴FE=FC,
∴△AEF,△EFC都是等腰三角形.
【解析】(1)根据要求作出图形;
(2)分两种情形:当∠B=∠BAE时,当B=∠AEB时,分别构建方程求解;
(3)在AC上取一点F,使得AE=EF即可.
本题考查作图−应用与设计作图,角平分线的性质,等腰三角形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.摸球的次数n
50
100
300
500
800
1000
2000
摸到红球的次数m
14
a
95
155
241
298
602
摸到红球的频率mn
0.28
0.33
0.317
0.31
0.301
0.298
b
课题
测量河两岸A、B两点间距离
测量工具
测量角度的仪器,皮尺等
测量方案示意图
测量步骤
①在点B所在河岸同侧的平地上取点C和点D,使得点A、B、C在一条直线上,且CD=BC;
②测得∠DCB=100°,∠ADC=65°;
③在CD的延长线上取点E,使得∠BEC=15°;
④测得DE的长度为30米.
氮肥施用量/kg
0
34
67
110
135
202
255
336
404
471
土豆产量/t
14.73
21.10
26.61
32.82
35.92
42.38
45.55
47.22
45.55
41.20
2023-2024学年河南省郑州市郑州东区七年级(下)期末数学试卷(含答案): 这是一份2023-2024学年河南省郑州市郑州东区七年级(下)期末数学试卷(含答案),共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
河南省郑州市郑州东区2023-2024学年七年级下学期数学期末试卷: 这是一份河南省郑州市郑州东区2023-2024学年七年级下学期数学期末试卷,共8页。
河南省郑州市郑州东区2023-2024学年七年级下学期数学期末试卷: 这是一份河南省郑州市郑州东区2023-2024学年七年级下学期数学期末试卷,共8页。












