考点21与圆有关的计算（精讲）-2024年中考数学一轮复习之核心考点精讲精练（全国通用）原卷版+解析版

这是一份考点21与圆有关的计算（精讲）-2024年中考数学一轮复习之核心考点精讲精练（全国通用）原卷版+解析版，文件包含考点21与圆有关的计算精讲原卷版-2024年中考数学一轮复习之核心考点精讲精练全国通用docx、考点21与圆有关的计算精讲解析版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。

从近年各地中考来，与圆相关的计算考查频率还是比较高，主要结合圆周角和圆心角相关知识围绕计算正多边形相关知识、弧长、扇形面积、不规则图形的面积及圆锥相关知识命题，题型主要以选填题为主，难度不大。预测2024年各地中考还会延续这种命题趋势，并也有可能出现创新型题目。
【知识清单】
1：正多边形的相关概念与计算（☆☆）
1）正多边形的相关概念
正多边形概念：各条边相等，并且各个内角也都相等的多边形叫做正多边形。
正多边形的中心：正多边形的外接圆的圆心叫做这个正多边形的中心。
正多边形的半径：正多边形外接圆的半径叫做正多边形的半径。
正多边形的中心角：正多边形每一边所对的圆心角叫做正多边形的中心角。
正多边形的边心距：中心到正多边形的一边的距离叫做正多边形的边心距。
2）正多边形的常用公式 （Rn为正多边形外接圆的半径）
边长：；周长：；边心距： ；面积： ；
内角度数：；外角/中心角度数：；边长、半径、边心距的关系： 。
注意：正多边形的内切圆与外接圆为同心圆.
2：弧长、扇形面积、圆锥的相关计算（☆☆☆）
1)设⊙O QUOTE 的半径为R，n° QUOTE 圆心角所对弧长为l，n为弧所对的圆心角的度数，则

（1）弧长公式： ；（2）扇形面积公式： 或 ．
（3）圆锥侧面积公式：S圆锥侧=πrl （其中l是圆锥的母线长，r是圆锥的底面半径）
（4）圆锥全面积公式：S圆锥全=πrl+πr2 （圆锥的表面积=扇形面积+底面圆面积）
注：圆锥的相关公式难以记忆，建议牢记圆锥与侧面展开图的图形形式，并理解侧面展开图与扇形之间的关系。相关公式在解题过程中进行推导。
3：不规则图形的面积的计算（☆☆☆）
求与圆有关的不规则图形的面积时，最基本的思想就是转化思想，即把所求的不规则的图形的面积转化为规则图形的面积。常用的方法有：割补法、等积变换法、图形变换法等。
【核心考点】
核心考点1. 正多边形的相关概念与计算
例1：（2023年江苏省无锡市中考数学真题）下列命题：①各边相等的多边形是正多边形；②正多边形是中心对称图形；③正六边形的外接圆半径与边长相等；④正n边形共有n条对称轴．其中真命题的个数是（ ）
A．4B．3C．2D．1
【答案】C
【分析】根据正多边形的性质以及正多边形与圆的关系逐一进行判断即可．
【详解】解：各边相等各角相等的多边形是正多边形，只有各边相等的多边形不一定是正多边形，如菱形，故①是假命题；
正三角形和正五边形就不是中心对称图形，故②为假命题；
正六边形中由外接圆半径与边长可构成等边三角形，所以外接圆半径与边长相等，故③为真命题；
根据轴对称图形的定义和正多边形的特点，可知正n边形共有n条对称轴，故④为真命题.故选：C．
【点睛】本题考查的是正多边形的概念以及正多边形与圆的关系，属于基础题型．
变式1.（2023·广东揭阳·统考一模）一个正多边形的中心角为36°，则这个正多边形的内角和为 度．
【答案】1440
【分析】依据正多边形的中心角和为求得边数，再依据多边形内角和公式代入求解即可．
【详解】解：因为正多边形的中心角为36°，且中心角和为，所以这个多边形边数：，
则这个多边形的内角和为：．故答案为：．
【点睛】本题考查了正多边形内角和公式、中心角性质，通过中心角求得边数是解题的关键．
变式2．（2023湖南省衡阳市中考数学真题）如图，用若干个全等的正五边形排成圆环状，图中所示的是其中3个正五边形的位置．要完成这一圆环排列，共需要正五边形的个数是 个．

【答案】10
【分析】先求出正五边形的外角为，则，进而得出，即可求解．
【详解】解：根据题意可得：∵正五边形的一个外角，∴，
∴，∴共需要正五边形的个数（个），故答案为：10．

【点睛】本题主要考查了圆的基本性质，正多边形的外角，解题的关键是掌握正多边形的外角的求法．
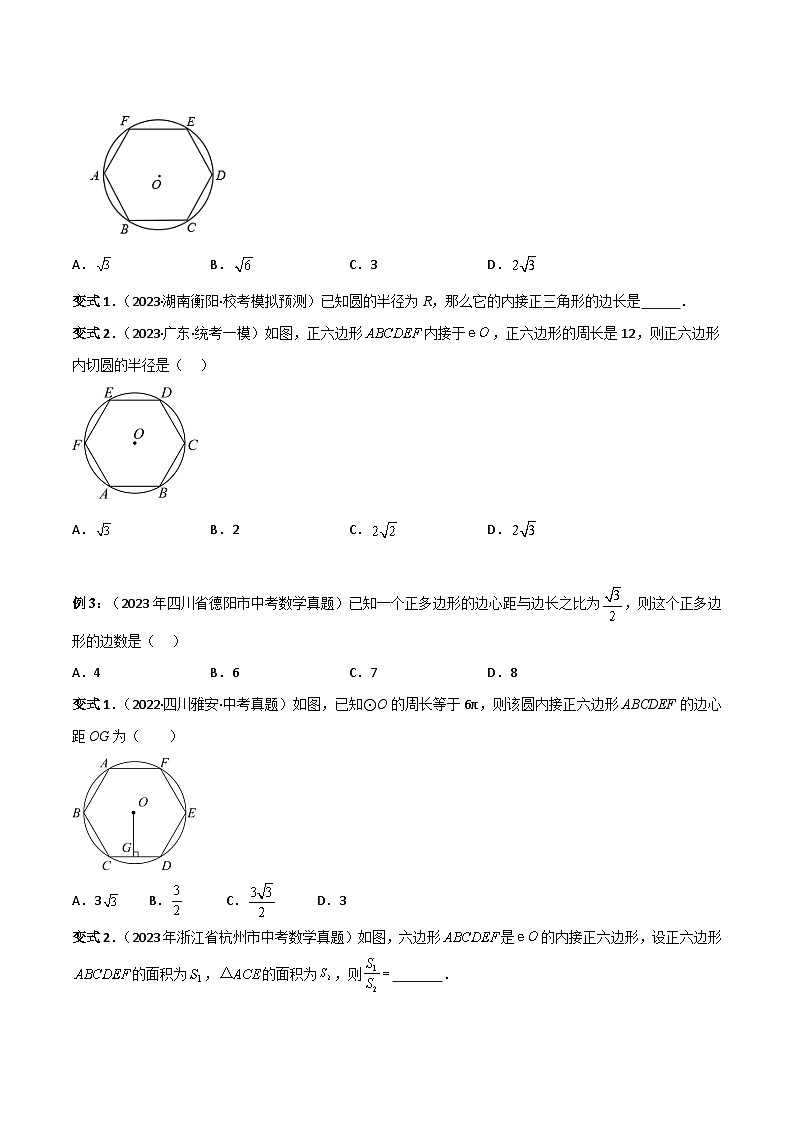
例2：（2022·四川成都·中考真题）如图，正六边形内接于⊙，若⊙的周长等于，则正六边形的边长为（ ）
A．B．C．3D．
【答案】C
【分析】连接OB，OC，由⊙O的周长等于6π，得⊙O的半径，又由圆的内接多边形的性质，即可求得答案．
【详解】解：连接OB，OC，
∵⊙O的周长等于6π，∴⊙O的半径为：3，∵∠BOC360°＝60°，∵OB＝OC，
∴△OBC是等边三角形，∴BC＝OB＝3，∴它的内接正六边形ABCDEF的边长为3，故选：C．
【点睛】此题考查了正多边形与圆的性质．此题难度适中，注意掌握数形结合思想的应用．
变式1．（2023·湖南衡阳·校考模拟预测）已知圆的半径为R，那么它的内接正三角形的边长是 ．
【答案】
【分析】根据正三角形外心的性质得，，，，再根据含30度直角三角形的性质及勾股定理求出边长即可．
【详解】解：如图所示，为正三角形外接圆的圆心，
，，，，
在中，，，，，
故答案为：
【点睛】本题考查圆与正多边形的相关计算，解题关键掌握正三角形外心的性质．
变式2．（2023·广东·统考一模）如图，正六边形内接于，正六边形的周长是12，则正六边形内切圆的半径是（ ）

A．B．2C．D．
【答案】A
【分析】根据已知条件先求出正六边形的边长以及对应角度，构建直角三角形，利用勾股定理即可求出答案．
【详解】解：连接、，过作于点，如图所示，

∵多边形是正六边形，正六边形的周长是12，∴，,
∵，∴是等边三角形，∴，
∵，∴,在中，，,
由勾股定理得，即正六边形内切圆的半径是；故选：．
【点睛】本题考查的是正多边形和圆，熟知正六边形的性质是解答此题的关键．
例3：（2023年四川省德阳市中考数学真题）已知一个正多边形的边心距与边长之比为，则这个正多边形的边数是（ ）
A．4B．6C．7D．8
【答案】B
【分析】如图，A为正多边形的中心，为正多边形的边，，为正多边形的半径，为正多边形的边心距，由可得，可得，而，可得为等边三角形，从而可得答案．
【详解】解：如图，A为正多边形的中心，为正多边形的边，，为正多边形的半径，为正多边形的边心距，

∴，，，∴，∴，即，
∴，∴，而，∴为等边三角形，
∴，∴多边形的边数为：，故选B
【点睛】本题考查的是正多边形与圆，锐角三角函数的应用，熟练的利用数形结合的方法解题是关键．
变式1．（2022·四川雅安·中考真题）如图，已知⊙O的周长等于6π，则该圆内接正六边形ABCDEF的边心距OG为（ ）
A．3B．C．D．3
【答案】C
【分析】利用圆的周长先求出圆的半径，正六边形的边长等于圆的半径，正六边形一条边与圆心构成等边三角形，根据边心距即为等边三角形的高用勾股定理求出OG．
【详解】∵圆O的周长为，设圆的半径为R，∴∴R=3
连接OC和OD，则OC=OD=3∵六边形ABCDEF是正六边形，

∴∠COD=，∴△OCD是等边三角形，OG垂直平分CD，
∴OC=OD=CD，∴故选 C
【点睛】本题考查了正多边形，熟练掌握圆内接正多边形的相关概念是解题的关键．
变式2．（2023年浙江省杭州市中考数学真题）如图，六边形是的内接正六边形，设正六边形的面积为，的面积为，则 ．

【答案】2
【分析】连接，首先证明出是的内接正三角形，然后证明出，得到，，进而求解即可．
【详解】如图所示，连接，

∵六边形是的内接正六边形，∴，∴是的内接正三角形，
∵，，∴，
∵，∴，∴，同理可得，，
又∵，∴，∴，
由圆和正六边形的性质可得，，由圆和正三角形的性质可得，，
∵，∴．答案：2．
【点睛】此题考查了圆内接正多边形的性质，正六边形和正三角形的性质，全等三角形的性质和判定等知识，解题的关键是熟练掌握以上知识点．
例4：（2023年安徽省舒城县中考模拟数学试题）如图，正六边形内接于，点在上，是的中点，则的度数为（ ）
A．B．C．D．
【答案】C
【分析】先计算正六边形的中心角，再利用同圆或等圆中，等弧对的圆心角相等，圆周角定理计算即可．
【详解】如图，连接，∵正六边形，是的中点，
∴，，
∴，∴，故选Ｃ．
【点睛】本题考查正多边形与圆，圆周角定理，熟练掌握正多边形中心角计算，圆周角定理是解题的关键．
变式1．（2023年安徽中考数学真题）如图，正五边形内接于，连接，则（ ）

A．B．C．D．
【答案】D
【分析】先计算正五边形的内角，再计算正五边形的中心角，作差即可．
【详解】∵，∴，故选D．
【点睛】本题考查了正五边形的外角，内角，中心角的计算，熟练掌握计算公式是解题的关键．
变式2．（2023·吉林长春·校联考二模）如图，正六边形内接于，点在上，则的大小为（ ）
A．60°B．45°C．30°D．15°
【答案】C
【分析】由正六边形的性质得出，由圆周角定理求出．
【详解】解：连接，，
∵多边形是正六边形，∴，∴，故选：C．
【点睛】本题考查了正六边形的性质，圆周角定理，熟练掌握知识点是解题的关键．
核心考点2.弧长、扇形面积、圆锥的相关计算
例5：（2023年四川省达州市中考数学真题）如图，四边形是边长为的正方形，曲线是由多段的圆心角的圆心为，半径为；的圆心为，半径为的圆心依次为循环，则的长是（ ）

A．B．C．D．
【答案】A
【分析】曲线是由一段段90度的弧组成的，半径每次比前一段弧半径，得到，，得出半径，再计算弧长即可．
【详解】解：由图可知，曲线是由一段段90度的弧组成的，半径每次比前一段弧半径，，，，，
，，，，，
，，
故的半径为，
的弧长．故选A
【点睛】此题考查弧长的计算，弧长的计算公式：，找到每段弧的半径变化规律是解题关键．
变式1. （2023.重庆中考模拟预测）如图，扇形的半径为1，分别以点A、B为圆心，大于的长为半径画弧，两弧相交于点P，，则的长 （结果保留π）．

【答案】/
【分析】先求解，再利用弧长公式计算即可．
【详解】解：由作图知：垂直平分，∵，∴，
∵扇形的半径是1，∴的长．故答案为：．
【点睛】本题考查的是线段的垂直平分线的作图，等腰三角形的性质，弧长的计算，熟记弧长公式是解本题的关键．
变式2．（2023年辽宁省大连市中考数学真题）圆心角为，半径为3的扇形弧长为（ ）
A．B．C．D．
【答案】C
【分析】根据弧长公式（弧长为l，圆心角度数为n，圆的半径为r），由此计算即可．
【详解】解：该扇形的弧长，故选：C．
【点睛】本题考查了扇形的弧长计算公式（弧长为l，圆心角度数为n，圆的半径为r），正确记忆弧长公式是解答此题的关键．
变式3.（2023年湖北省荆州市中考数学真题）如图，一条公路的转弯处是一段圆弧（），点是这段弧所在圆的圆心，为上一点，于．若，，则的长为（ ）

A．B．C．D．
【答案】B
【分析】据垂径定理求出长度，再根据勾股定理求出半径长度，最后利用弧长公式即可求出答案.
【详解】解： ，点是这段弧所在圆的圆心，，，
，，，.
，，.设，则，
在中，，，.
，，.故选：B.
【点睛】本题考查了圆的垂径定理，弧长公式，解题的关键在于通过勾股定理求出半径长度，从而求出所求弧长所对应的圆心角度数.
例6：（2023年山东省济南市中考数学真题）如图，正五边形的边长为，以为圆心，以为半径作弧，则阴影部分的面积为 （结果保留）．

【答案】
【分析】根据正多边形内角和公式求出正五边形的内角和，再求出的度数，利用扇形面积公式计算即可．
【详解】解：正五边形的内角和，
，，故答案为：．
【点睛】本题考查了扇形面积和正多边形内角和的计算，熟练掌握扇形面积公式和正多边形内角和公式是解答本题的关键．
变式1．（2022·四川达州·中考真题）如图所示的曲边三角形可按下述方法作出：作等边，分别以点A，B，C为圆心，以长为半径作，，，三弧所围成的图形就是一个曲边三角形．如果一个曲边三角形的周长为，则此曲边三角形的面积为（ ）
A．B．C．D．
【答案】A
【分析】根据此三角形是由三段弧组成，所以根据弧长公式可得半径，即正三角形的边长，根据曲边三角形的面积等于三角形的面积与三个弓形的面积和，边长为的等边三角形的面积为，即可求解．
【详解】解：设等边三角形ABC的边长为r，
解得，即正三角形的边长为2，
此曲边三角形的面积为 故选A
【点睛】本题考查了扇形面积的计算．此题的关键是明确曲边三角形的面积等于三角形的面积与三个弓形的面积和，然后再根据所给的曲线三角形的周长求出三角形的边长．
变式2．（2023年辽宁省锦州市中考数学真题）如图，点A，B，C在上，，连接，．若的半径为3，则扇形（阴影部分）的面积为（ ）

A．B．C．D．
【答案】D
【分析】先利用圆周角定理求出的度数，然后利用扇形面积公式求解即可．
【详解】解：∵，∴，
又的半径为3，∴扇形（阴影部分）的面积为．故选：D．
【点睛】本题考查的是圆周角定理，扇形面积公式等，掌握“同弧所对的圆周角是它所对的圆心角的一半”是解题的关键．
例7：（2023年黑龙江省牡丹江市中考数学真题）用一个圆心角为，半径为8的扇形作一个圆锥的侧面，则这个圆锥的底面直径是（ ）
A．6B．5C．4D．3
【答案】C
【分析】先利用弧长公式求出扇形的弧长即圆锥的底面周长，再根据圆的周长公式求出直径即可．
【详解】解：扇形的弧长：，则圆锥的底面直径：．故选：C．
【点睛】本题考查圆锥侧面积公式，熟记公式的灵活应用是解题的关键．
变式1．（2023年西藏自治区中考数学真题）圆锥的底面半径是，母线长，则它的侧面展开图的圆心角的度数为 ．
【答案】
【分析】设圆锥的侧面展开图的圆心角为，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到，然后解关于的方程即可．
【详解】解：设圆锥的侧面展开图的圆心角为，
根据题意得解得，即圆锥的侧面展开图的圆心角为．故答案为：．
【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
变式2．（2023年浙江省宁波市中考数学真题）如图，圆锥形烟囱帽的底面半径为，母线长为，则烟囱帽的侧面积为 ．（结果保留）

【答案】
【分析】根据圆锥侧面展开图是一个扇形，由扇形面积公式代值求解即可得到答案．
【详解】解：圆锥形烟囱帽的底面半径为，母线长为，
烟囱帽的侧面积（），故答案为：．
【点睛】本题考查圆锥侧面展开图及扇形面积公式，熟记扇形面积公式是解决问题的关键．
变式3．（2023年云南省中考数学真题）数学活动课上，某同学制作了一顶圆锥形纸帽．若圆锥的底面圆的半径为1分米，母线长为4分米，则该圆锥的高为 分米．
【答案】
【分析】根据勾股定理得，圆锥的高=母线长底面圆的半径得到结果．
【详解】解：由圆锥的轴截面可知：圆锥的高=母线长底面圆的半径
圆锥的高，故答案为．
【点睛】本题考查了圆锥，勾股定理，其中对圆锥的高，母线长，底面圆的半径之间的关系的理解是解决本题的关键．
例8：（2023年内蒙古赤峰市中考数学真题）某班学生表演课本剧，要制作一顶圆锥形的小丑帽．如图，这个圆锥的底面圆周长为，母线长为30，为了使帽子更美观，要粘贴彩带进行装饰，其中需要粘贴一条从点A处开始，绕侧面一周又回到点A的彩带（彩带宽度忽略不计），这条彩带的最短长度是（ ）

A．B．C．D．
【答案】B
【分析】根据圆锥的底面圆周长求得半径为，根据母线长求得展开后的扇形的圆心角为，进而即可求解．
【详解】解：∵这个圆锥的底面圆周长为，∴解得：
∵解得：∴侧面展开图的圆心角为
如图所示，即为所求，过点作，∵，，则
∵，则∴，，故选：B．

【点睛】本题考查了圆锥侧面展开图的圆心角的度数，勾股定理解直角三角形，求得侧面展开图的圆心角为解题的关键．
变式1．（2023·广东湛江·统考一模）如图，已知圆锥底面圆的半径为，母线长为，一只蚂蚁从点A出发沿圆锥侧面一周（回到原来的位置A）所爬行的最短路径为 ．

【答案】
【分析】本题考查了圆锥侧面展开图的圆心角，把圆锥的侧面展开得到圆心角为，半径为的扇形，求出扇形中的圆心角所对的弦长即为最短路径．将圆锥中的数据对应到展开图中是解题的关键．
【详解】解：圆锥的侧面展开如图，过点S作，

∴，设，即：，得：，
∵，，∴，∴
∴，∴．故答案为：．
变式2.（2023·江苏扬州·统考二模）如图，已知圆锥的底面半径是，母线长是．如果A是底面圆周上一点，从点A拉一根绳子绕圆锥侧面一圈再回到A点，则这根绳子的最短长度是 ．
【答案】18
【分析】连接AC，过B作BD⊥AC于D，设圆锥的侧面展开图扇形的圆心角∠ABC为n．利用弧长公式可求出n的值，根据两点间线段最短可得AC为这根绳子的最短长度，根据等腰三角形的性质，利用∠CBD的正弦值求出AC的长即可得答案．
【详解】如图，连接AC，过B作BD⊥AC于D，设圆锥的侧面展开图扇形的圆心角为n．
∵两点间线段最短，∴AC为这根绳子的最短长度，
∵圆锥的底面半径是，∴，∴=，解得：，
∵BD⊥AC，BC=AB，∴∠CBD=∠ABC=60°，CD=AC，
∴CD=BC·sin60°=×=9，∴AC=2CD=18，故答案为：18
【点睛】此题考查了圆锥的计算、等腰三角形的性质及特殊角的三角函数值，熟练掌握圆锥的底面圆的周长和扇形弧长相等并熟记特殊角的三角函数值是解题关键．
核心考点3.不规则图形的面积的计算
例9：（2023年四川省成都市数学中考真题）为传承非遗文化，讲好中国故事，某地准备在一个场馆进行川剧演出．该场馆底面为一个圆形，如图所示，其半径是10米，从A到B有一笔直的栏杆，圆心O到栏杆的距离是5米，观众在阴影区域里观看演出，如果每平方米可以坐3名观众，那么最多可容纳 名观众同时观看演出．（取3.14，取1.73）

【答案】184
【分析】过点O作的垂线段，交于点，根据直角三角形的边长关系求出的角度，阴影面积即为扇形的面积减去三角形的面积，随机可以求出容纳观众的数量．
【详解】解：如图，过点O作的垂线段，交于点，

圆心O到栏杆的距离是5米，米，
，，米， ，
，，可容纳的观众
阴影部分面积（人），
最多可容纳184名观众同时观看演出，故答案为：184．
【点睛】本题考查弓形的面积，根据特殊角三角函数值求角的度数，熟知扇形面积公式是解题的关键．
变式1. （2023年重庆市中考数学真题（B卷））如图，在矩形中，，，E为的中点，连接，以E为圆心，长为半径画弧，分别与交于点M，N，则图中阴影部分的面积为 ．（结果保留）

【答案】
【分析】利用矩形的性质求得，进而可得，然后根据解答即可．
【详解】解：∵四边形是矩形，，，E为的中点，
∴，，∴，
∴；故答案为：．
【点睛】本题考查了矩形的性质和不规则面积的计算，熟练掌握矩形的性质、明确阴影面积为两个全等的等腰直角三角形的面积减去两个圆心角为的扇形面积是解题关键．
变式2.（2023年青海省中考数学真题）如图，正方形ABCD的边长是4，分别以点A，B，C，D为圆心，2为半径作圆，则图中阴影部分的面积是 （结果保留）.

【答案】/
【分析】分析出阴影面积正方形面积圆的面积，再利用相应的面积公式计算即可．
【详解】解：由图得，阴影面积正方形面积个扇形面积，
即阴影面积正方形面积圆的面积，．故答案为：．
【点睛】本题考查了扇形面积的求法，正方形面积及圆的面积的求法是解题关键．
例10：（2023年内蒙古包头市中考数学真题）如图，正方形的边长为2，对角线相交于点，以点为圆心，对角线的长为半径画弧，交的延长线于点，则图中阴影部分的面积为 ．

【答案】
【分析】根据正方形的性质得出阴影部分的面积为扇形的面积，然后由勾股定理得出，再由扇形的面积公式求解即可．
【详解】解：正方形，∴，，∴，
∵正方形的边长为2，∴
∴阴影部分的面积为扇形的面积，即，故答案为：．
【点睛】本题考查正方形的性质及扇形的面积公式，理解题意，将阴影部分面积进行转化是解题关键．
变式1.（2023年山东省滨州市中考数学真题）如图，某玩具品牌的标志由半径为的三个等圆构成，且三个等圆相互经过彼此的圆心，则图中三个阴影部分的面积之和为（ ）

A．B．C．D．
【答案】C
【分析】根据圆的对称性可知：图中三个阴影部分的面积相等，只要计算出一个阴影部分的面积即可，如图，连接，阴影的面积＝扇形的面积，据此即可解答.
【详解】解：根据圆的对称性可知：图中三个阴影部分的面积相等；
如图，连接，则，是等边三角形，
∴，弓形的面积相等，
∴阴影的面积＝扇形的面积，
∴图中三个阴影部分的面积之和；故选：C.

【点睛】本题考查了不规则图形面积的计算，正确添加辅助线、掌握求解的方法是解题关键.
变式2.（2023年湖北省恩施州中考数学真题）如图，等圆和相交于A，B两点，经过的圆心，若，则图中阴影部分的面积为（ ）
A．B．C．D．
【答案】D
【分析】先证明，再把阴影部分面积转换为扇形面积，最后代入扇形面积公式即可．
【详解】如图，连接，，
∵等圆和相交于A，B两点∴,
∵和是等圆∴∴是等边三角形∴
∵,,∴
∴．故选：D．
【点睛】本题考查了相交弦定理，全等的判定及性质，扇形的面积公式，转化思想是解题的关键．
变式3．（2023年湖南省娄底市中考数学真题）如图，正六边形的外接圆的半径为2，过圆心O的两条直线、的夹角为，则图中的阴影部分的面积为（ ）

A．B．C．D．
【答案】C
【分析】如图，连接，标注直线与圆的交点，由正六边形的性质可得：，，三点共线，为等边三角形，证明扇形与扇形重合，可得，从而可得答案．
【详解】解：如图，连接，标注直线与圆的交点，
由正六边形的性质可得：，，三点共线，为等边三角形，

∴，，∴，
∴扇形与扇形重合，∴，
∵为等边三角形，，过作于，
∴，，，
∴；故选C
【点睛】本题考查的是正多边形与圆，扇形面积的计算，勾股定理的应用，熟记正六边形的性质是解本题的关键．
例11：（2023年四川省广安市中考数学真题）如图，在等腰直角中，，以点为圆心，为半径画弧，交于点，以点为圆心，为半径画弧，交于点，则图中阴影部分的面积是（ ）

A．B．C．D．
【答案】C
【分析】先利用扇形的面积公式求出扇形和扇形的面积，再减去的面积即可得．
【详解】解：是等腰直角三角形，，
，∴图中阴影部分的面积是
，故选：C．
【点睛】本题考查了扇形的面积，熟练掌握扇形的面积公式是解题关键．
变式1. （2023年湖北省鄂州市中考数学真题）如图，在中，，，，点为的中点，以为圆心，长为半径作半圆，交于点，则图中阴影部分的面积是（ ）

A．B．C．D．
【答案】C
【分析】连接，，作交于点，首先根据勾股定理求出的长度，然后利用解直角三角形求出、的长度，进而得到是等边三角形，，然后根据角直角三角形的性质求出的长度，最后根据进行计算即可．
【详解】解：如图所示，连接，，作交于点

∵在中，，，，∴，
∵点为的中点，以为圆心，长为半径作半圆，∴是半圆的直径，∴，
∵，∴，，
又∵，∴，∴是等边三角形，∴，
∵，，∴，
∴．故选：C．
【点睛】本题考查了角直角三角形的性质，解直角三角形，等边三角形的性质和判定，扇形面积，勾股定理等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键．
变式2.（2022·湖北十堰·中考真题）如图，扇形中，，，点为上一点，将扇形沿折叠，使点的对应点落在射线上，则图中阴影部分的面积为_________．
【答案】2π+4–4
【分析】连接AB，在Rt△AOB中，由勾股定理，求得AB=，由折叠可得：，，则，设OC=x，则=2-x，在Rt△CO中，由勾股定理，得，解得：x=，最后由S阴影=S扇形-2S△AOC求解即可．
【详解】解：连接AB，
在Rt△AOB中，由勾股定理，得AB=，
由折叠可得：，，∴，设OC=x，则=2-x，
在Rt△CO中，由勾股定理，得，解得：x=，
S阴影=S扇形-2S△AOC===2π+4–4，故答案为：2π+4–4．
【点睛】本题考查折叠的性质，勾股定理，扇形的面积，利用折叠的性质和勾股定理求出OC长是解题关键．
变式3．（2023·河南周口·统考二模）如图所示的是以为直径的半圆形纸片，，沿着垂直于的半径剪开，将扇形沿向右平移至扇形，如图，其中点与点重合，点与点重合，则图中阴影部分的面积为 ．
【答案】
【分析】连接，作于点，，即可求得弧和以及围成的重叠部分的面积，则重叠部分的面积即可求得．
本题考查了扇形的面积的计算，正确理解不规则的图形的面积转化为规则图形的面积的和、差计算是关键．
【详解】解：连接，作于点．
，，，，
在直角中，，则，
则弧和以及围成的阴影部分的面积是：，
则．故答案是：．
例12：（2023年江苏省苏州市中考数学真题）如图，在中，，垂足为．以点为圆心，长为半径画弧，与分别交于点．若用扇形围成一个圆锥的侧面，记这个圆锥底面圆的半径为；用扇形围成另一个圆锥的侧面，记这个圆锥底面圆的半径为，则 ．（结果保留根号）

【答案】/
【分析】由，，，，，，，，求解，，证明，可得，再分别计算圆锥的底面半径即可．
【详解】解：∵在中，，，
∴，，∵，，
∴，，∴，
∵，∴，∴，，
解得：，，∴；故答案为：
【点睛】本题考查的是平行四边形的性质，勾股定理的应用，锐角三角函数的应用，扇形的弧长的计算，圆锥的底面半径的计算，熟记圆锥的侧面展开图的扇形弧长等于底面圆的周长是解本题的关键．
变式1. （2023·吉林白山·统考一模）如图，在半径为5，圆心角为的扇形中，阴影部分的面积；在半径为2的圆中，阴影部分的面积为，则 （结果保留π）．
【答案】
【分析】此题主要考查了扇形面积公式以及阴影部分面积求法，正确转化阴影图形的形状是解题关键．由图形可知等于半径为5，圆心角为的扇形的面积减去半径为2的圆的面积．
【详解】解：，故答案为．
变式2.（2022·湖南娄底·中考真题）如图，等边内切的图形来自我国古代的太极图，等边三角形内切圆中的黑色部分和白色部分关于等边的内心成中心对称，则圆中的黑色部分的面积与的面积之比是（ ）
A．B．C．D．
【答案】A
【分析】由题意，得圆中黑色部分的面积是圆面积的一半，令BC=2a，则BD=a，根据勾股定理，得出AD=，同时在Rt△BOD中，OD=，进而求出黑色部分的面积以及等边三角形的面积，最后求出答案．
【详解】解：令内切圆与BC交于点D，内切圆的圆心为O，连接AD，OB，
由题可知，圆中黑色部分的面积是圆面积的一半，
令BC=2a，则BD=a，在等边三角形ABC中AD⊥BC，OB平分∠ABC，∴∠OBD=∠ABC=30°，
由勾股定理，得AD=，在Rt△BOD中，OD=tan30°×BD=，
∴圆中的黑色部分的面积与的面积之比为．故选：A．
【点睛】本题考查了等边三角形的性质，内切圆的性质和面积，等边三角形的面积以及勾股定理求边长，正确地计算能力是解决问题的关键．