四川省内江市第一中学2024届九年级下学期中考一模数学试卷(含解析)

这是一份四川省内江市第一中学2024届九年级下学期中考一模数学试卷(含解析)，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．的倒数是（ ）
A．B．C．D．
2．人的大脑每天能记录大约条信息，用科学记数法表示为（ ）
A．B．C．D．
3．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
4．如图，，点在线段上（不与点，重合），连接，若，，则（ ）

A．B．C．D．
5．下列运算结果正确的是（ ）
A．B．C．D．
6．如图所示的几何体的左视图是( )
A．B．C．D．
7．在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表：
这些运动员跳高成绩的中位数和众数分别是（ ）
A．1.65，1.70B．1.70，1.65C．1.70，1.70D．3，5
8．在函数y＝中，自变量x的取值范围是（ ）
A．x≥3B．x≥﹣3C．x≥3且x≠0D．x≥﹣3且x≠0
9．《孙子算经》是中国古代重要的数学著作，是《算经十书》之一．书中记载了这样一个题目：今有木，不知长短．引绳度之，余绳四尺五寸；屈绳量之，不足一尺．木长几何？其大意是：用一根绳子去量一根长木，绳子还剩余尺；将绳子对折再量长木，长木还剩余尺．问木长多少尺？设木长尺，则可列方程为（ ）
A．B．
C．D．
10．如图，平行四边形中以点为圆心，适当长为半径作弧，交于，分别以点为圆心大于长为半作弧，两弧交于点，作交于点，连接，若，则的长为（ ）
A．B．C．D．
11．如图，在矩形中，，，点E、F分别为、的中点，、相交于点G，过点E作，交于点H，则线段的长度是（ ）
A．B．1C．D．
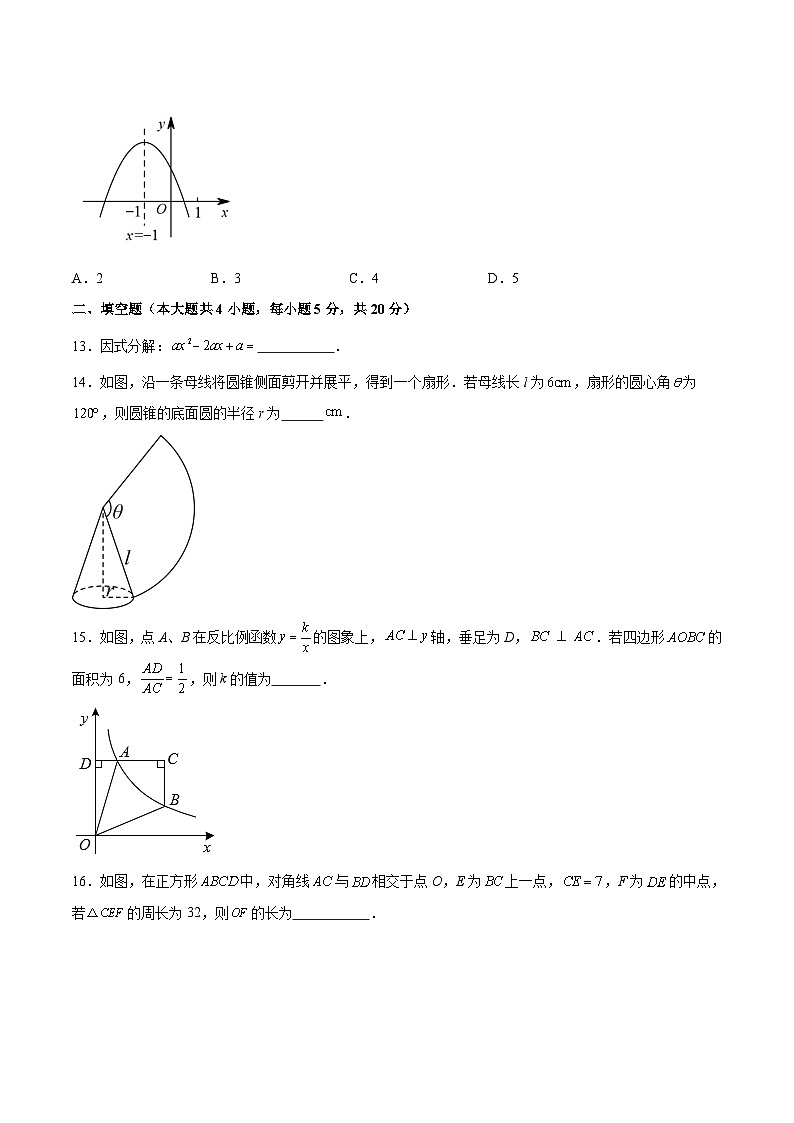
12．已知二次函数的图象如图所示，以下结论中：①；②；③；④（的任意实数）；⑤．正确的个数是（ ）
A．2B．3C．4D．5
二、填空题（本大题共4小题，每小题5分，共20分）
13．因式分解： ．
14．如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形．若母线长l为，扇形的圆心角为，则圆锥的底面圆的半径r为 ．

15．如图，点A、B在反比例函数的图象上，轴，垂足为D，．若四边形的面积为6，，则k的值为 ．
16．如图，在正方形中，对角线与相交于点O，E为上一点，，F为的中点，若的周长为32，则的长为 ．

三、解答题（本大题共5小题，共44分，解答应写出必要的文字说明或推演步骤）
17．计算：
18．如图，中，点D是AB上一点，点E是AC的中点，过点C作，交DE的延长线于点F．
(1)求证：；
(2)连接AF，CD．如果点D是AB的中点，那么当AC与BC满足什么条件时，四边形ADCF是菱形，证明你的结论．
19．某校组织学生观看“天宫课堂”第二课直播，跟着空间站的翟志刚、王亚平、叶光富三位宇航员学习科学知识，他们相互配合，生动演示了四个实验：（A）微重力环境下的太空“冰雪”实验，（B）液桥演示实验，（C）水油分离实验，（D）太空抛物实验．观看完后，该校对部分学生对四个实验的喜爱情况作了抽样调查，将调查情况制成了如下的条形统计图和扇形统计图．
请根据图中信息，回答下列问题：
(1)共调查了_________名学生，图2中A所对应的圆心角度数为_________；
(2)请补全条形统计图；
(3)若从两名男生、两名女生中随机抽取2人参加学校组织的“我爱科学”演讲比赛，请用列表或画树状图的方法，求抽到的学生恰好是一男一女的概率．
20．综合与实践活动中，要利用测角仪测量塔的高度，如图，塔AB前有一座高为DE的观骨台，已知，，点E，C，A在同一条水平直线上．某学习小组在观景台C处测得塔顶部B的仰角为45°，在观景台D处测得塔顶部B的仰角为27°．

(1)求的长；
(2)求塔的高度．（取0.5，取1.7，结果取整数）
21．如图，一次函数与反比例函数的图象交于A、两点，点A坐标为，点坐标为，直线交轴于点，过作轴的垂线，交反比例函数图象于点，连接、．
(1)求一次函数与反比例函数的解析式；
(2)请你根据图象直接写出不等式的解集，
(3)求四边形的面积．
B卷（共60分）
四、填空题（本大题共4小题，每小题6分，共24分）
22．若m，n为方程的两根，则多项式的值为 ．
23．若关于x的一元一次不等式组有且仅有3个整数解，且关于x的分式方程有正数解，则所有满足条件的整数a的和为 ．
24．如图，在第一象限内的直线：上取点，使，以为边作等边，交轴于点；过点作轴的垂线交直线于点，以为边作等边，交轴于点；过点作轴的垂线交直线于点，以为边作等边，交轴于点；…，依次类推，则点的横坐标为 ．
25．如图，的半径为4，圆心M的坐标为，点P是上的任意一点，，且、与x轴分别交于A、B两点．若点A、点B关于原点O对称，则当取最大值时，点A的坐标为 ．

五、解答题（本大题共3小题，每小题12分，共36分）
26．随着“双减”政策的逐步落实，其中增加中学生体育锻炼时间的政策引发社会的广泛关注，体育用品需求增加，某商店决定购进A、B两种羽毛球拍进行销售，已知每副A种球拍的进价比每副B种球拍贵20元，用2800元购进A种球拍的数量与用2000元购进B种球拍的数量相同．
(1)求A、B两种羽毛球拍每副的进价；
(2)若该商店决定购进这两种羽毛球拍共100副，考虑市场需求和资金周转，用于购买这100副羽毛球拍的资金不超过5900元，那么该商店最多可购进A种羽毛球拍多少副？
(3)若销售A种羽毛球拍每副可获利润25元，B种羽毛球拍每副可获利润20元，在第（2）问条件下，如何进货获利最大？最大利润是多少元？
27．如图，以的边上一点为圆心的圆，经过两点，且与边交于点，，连接交于点，若．
(1)求证：是的切线；
(2)若，，求的长；
(3)在（2）的条件下，若，求阴影部分的面积．
28．如图，在平面直角坐标系中，点、在轴上，点、在轴上，且，，抛物线经过三点，直线与抛物线交于另一点．
(1)求这条抛物线的解析式；
(2)在抛物线对称轴上是否存在一点，使得的周长最小，若存在，请求出点的坐标，若不存在，请说明理由；
(3)点是直线上一动点，点为抛物线上直线下方一动点，当线段的长度最大时，请求出点的坐标和面积的最大值．
参考答案与解析
1．C
解答：解：的倒数为．
故选C．
2．B
解答：解：用科学记数法表示为，
故选：B．
3．C
解答：A、不是轴对称图形，是中心对称图形，故此选项不合题意；
B、是轴对称图形，不是中心对称图形，故此选项不合题意；
C、是轴对称图形，是中心对称图形，故此选项符合题意；
D、是轴对称图形，不是中心对称图形，故此选项不合题意；
答案：C．
4．B
解答：解：∵，，
∴，
∵，
∴，
故选：B．
5．C
解答：解：A、，选项计算错误，不符合题意；
B、，选项计算错误，不符合题意；
C、，选项计算正确，符合题意；
D、，选项计算错误，不符合题意；
故选C．
6．B
解答：解：从左边看，可得如图：
．
故选：B．
7．A
解答：解：∵共有15名运动员，按照从小到大进行排列后，第8个数据即为中位数，
∴中位数为：1.65
∵1.70出现的次数最多，
∴众数为：1.70
故选A．
8．D
解答：解：由题意得：x+3≥0且x≠0，
解得：x≥﹣3且x≠0，
故选：D．
9．A
解答：解：设木长尺，根据题意得，
，
故选：A
10．D
解答：解：如图，过点作交于．
四边形是平行四边形，
，
，
，，
四边形是平行四边形，
，
平分，
，
，
，，，
，
，
，
，
，
，
，
，
故选：D．
11．A
解答：解析：四边形是矩形，，，
，，，
点E、F分别为、的中点，
，，
，
，
，
．
由勾股定理得：，
，
，
，
，
，
解得：，
故选：A．
12．C
解答：解：由图象得：，，，
∴，故①正确；
由图象知：二次函数图象与x轴有两个交点，
∴，故②正确；
∵图象对称轴为直线，
∴，故③正确；
当时，该函数图象有最高点，即函数有最大值，此时，
当（的任意实数）时，，
∴，即，故④正确；
∵图象对称轴为直线，
∴与时的函数值相等，
∴当时函数值大于零，即，故⑤错误；
综上分析可知，正确的有4个，故C正确．
故选：C．
13．
解答：解：
，
故答案为：．
14．2
解答：解：由题意得：母线长l为，，
，
∴，
故答案为：2．
15．3
解答：解∶设点，
∵轴，
∴，，
∵，
∴，
∴CD=3a，
∵．轴，
∴BC∥y轴，
∴点B，
∴，
∵，四边形间面积为6，
∴，
解得：．
故答案为：3．
16．
解答：解：的周长为32，
．
为DE的中点，
．
，
，
，
，
．
四边形是正方形，
，O为BD的中点，
是的中位线，
．
故答案为：．
17．6
解答：解：原式
．
18．(1)见解析
(2)当时，四边形ADCF是菱形，证明见解析
解答：（1）证明：∵，
∴∠ADF=∠CFD，∠DAC=∠FCA．
∵点E是AC的中点，
∴AE=CE，
∴，
∴；
（2）解：当时，四边形ADCF是菱形．
证明如下：
由（1）知，，
∵，
∴四边形ADCF是平行四边形．
∵，
∴是直角三角形．
∵点D是AB的中点，
∴，
∴四边形ADCF是菱形．
19．(1)50，；
(2)详见解析；
(3)，详见解析．
解答：（1）共调查的学生人数为：（名），
∴图2中A所对应的圆心角度数为：，
故答案为：；
（2）（2）由图知，D的人数为：（人），
∴C的人数为：（人），
补全条形统计图如下：
（3）（3）画树状图如下：
共有12种等可能的结果，其中抽到的学生恰好是一男一女的结果有8种，
∴抽到的学生恰好是一男一女的概率为．
20．(1)3m
(2)塔的高度约为
解答：（1）解：在中，，
∴．
即的长为．
（2）设，
在中，，
∴．
在中，由，，，
则.
∴．
即的长为．
如图，过点作，垂足为．

根据题意，，
∴四边形是矩形．
∴，．
可得．
在中，，，
∴．即．
∴．
答：塔的高度约为．
21．(1)一次函数表达式为，反比例函数表达式为
(2)或
(3)18
解答：（1）解：点坐标为，
，
点在反比例函数图象上，
，
解得，
点坐标为，
将点，点代入一次函数，
得，
解得，
一次函数表达式为，反比例函数表达式为；
（2）由图象可知，不等式的解集是或．
（3）当时，，
点坐标为，
轴，
点纵坐标为，
点在反比例函数上，
点横坐标为，
，
四边形的面积
22．30
解答：解：∵m为方程的根，
∴，
∴，
∴，
∵m，n为方程的两根，
∴，
∴．
故答案为：30．
23．13
解答：
解不等式①得：x＜5，
解不等式②得：x≥，
∴不等式组的解集为≤x＜5，
∵不等式组有且仅有3个整数解，
∴1＜≤2，
∴2＜a≤6；
分式方程两边都乘以（x-1）得：ax-2-3=x-1，
解得：x= ，
∵x-1≠0，
∴x≠1，
∵方程有正数解，
∴＞0，≠1，
∴a＞1，a≠5，
∴2＜a≤6，且a≠5，
∴a的整数解为3，4，6，和为13．
故答案为：13．
24．
解答：解：，是等边三角形，
，
的横坐标为，
，
的横坐标为1，
过点作轴的垂线交直线于点，以为边作等边，交轴于点，过点作轴的垂线交直线于点，
，
的横坐标为2，
依此类推：的横坐标为
的横坐标为，
故答案为：．
25．
解答：解：连接，
∵，
∴，
∵点、点关于原点对称，
∴，
∴，
若要使取得最大值，则需取得最大值，
连接，并延长交于点，当点位于位置时，取得最大值，
过点作轴于点，

则、，
∴，
又∵，
∴，
∴；
∴，
即点A的坐标为，
故答案为：．
26．(1)A种羽毛球拍每副的进价为70元，B种羽毛球拍每副的进价为50元
(2)45副
(3)购进A种羽毛球拍45副，B种羽毛球拍55副时，总获利最大，最大利润为2225元
解答：（1）解：设A种羽毛球拍每副的进价为x元，
根据题意，得，
解得，经检验是原方程的解，
（元），
答：A种羽毛球拍每副的进价为70元，B种羽毛球拍每副的进价为50元；
（2）设该商店购进A种羽毛球拍m副，
根据题意，得，
解得，m为正整数，
答：该商店最多购进A种羽毛球拍45副；
（3）设总利润为w元，
，
∵，
∴w随着m的增大而增大，
当时，w取得最大值，最大利润为（元），
此时购进A种羽毛球拍45副，B种羽毛球拍（副），
答：购进A种羽毛球拍45副，B种羽毛球拍55副时，总获利最大，最大利润为2225元．
27．(1)见解答
(2)
(3)
解答：（1）证明：连接，
，
，
，
，
，
，
，
，，，
，
即是的切线．
（2）解：设的半径为，
，
，
，
，
在中，由勾股定理得，
，
，
解得：或（不符合题意舍），
∴；
（3）解： ，
，
，
，
，
在中，．
，
，
，，
．
28．(1)抛物线的解析式为；
(2)时的周长最小；
(3)当面积最大时，点的坐标为，面积最大值为．
解答：（1）∵，，
∴点的坐标为，点的坐标为，点的坐标为 ，点的坐标为 ，
将，，代入得：
，解得：，
∴这条抛物线的解析式为；
（2）∵，
∴抛物线的对称轴为直线，
连接，交抛物线对称轴点，如图所示，
∵点，关于直线对称，
∴，
∴
∴当点，，三点共线时，取得最小值，即的周长最小，
设直线的解析式为，
将，代入得：
，解得：，
∴直线的解析式为，
当时，，
∴在这条抛物线的对称轴上存在点时的周长最小；
（3）∵，，
∴直线的解析式为，联立直线和抛物线的解析式成方程组，得：，
解得：，，
∴点的坐标为，
过点作轴，交直线于点，如图所示，
设点的坐标为，则点的坐标为，
∴，
∴，
，
，
，
∵，
∴当时，的面积取最大值，最大值为，
∴当面积最大时，点的坐标为，面积最大值为．跳高成绩（m）
1.50
1.55
1.60
1.65
1.70
1.75
跳高人数
1
3
2
3
5
1