华师大版九年级上册1. 相似三角形说课ppt课件

这是一份华师大版九年级上册1. 相似三角形说课ppt课件，共24页。

专项素养综合全练（四）
相似三角形判定的六种常见模型
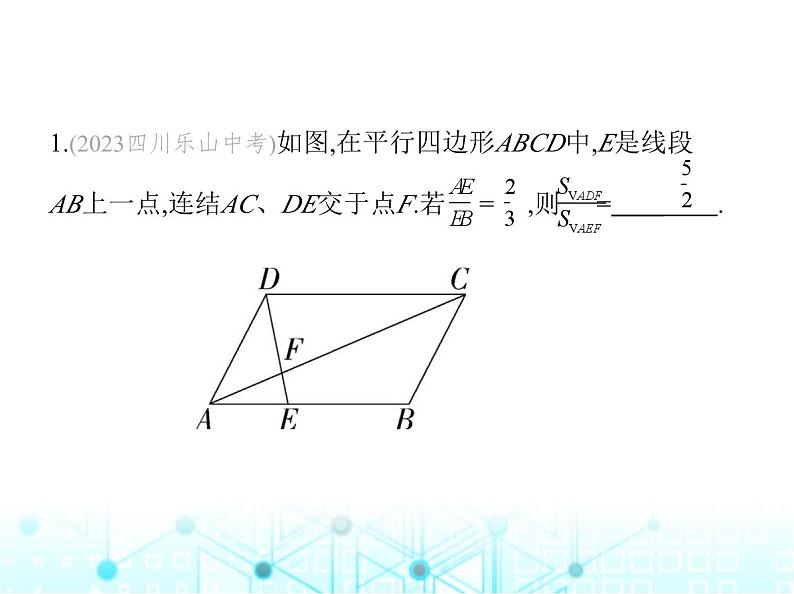
模型展示条件:DE∥BC.结论:△ADE∽△ABC.      
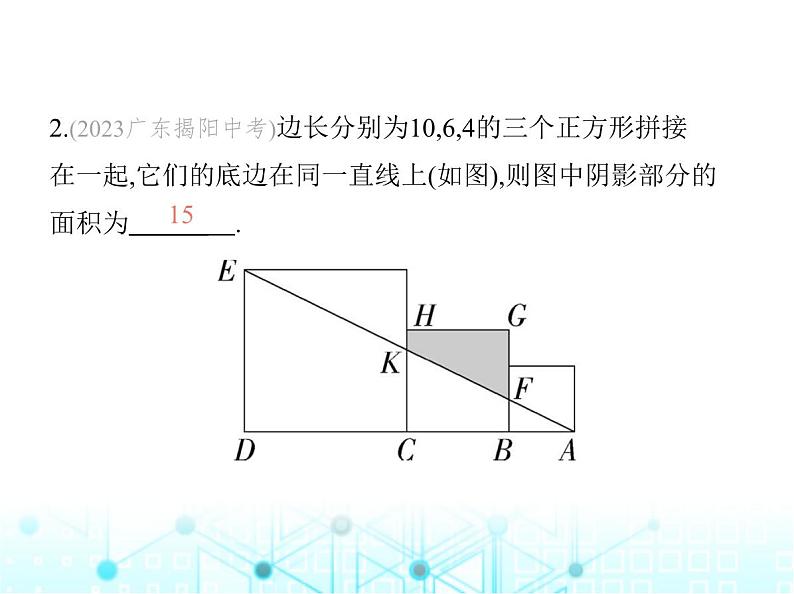
1.(2023四川乐山中考)如图,在平行四边形ABCD中,E是线段 AB上一点,连结AC、DE交于点F.若 = ,则 =　　        .  
解析　∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵  = ,∴设AE=2a,则BE=3a,∴AB=CD=5a,∵AB∥CD,∴△AEF∽△CDF,∴ = = ,∴ = .
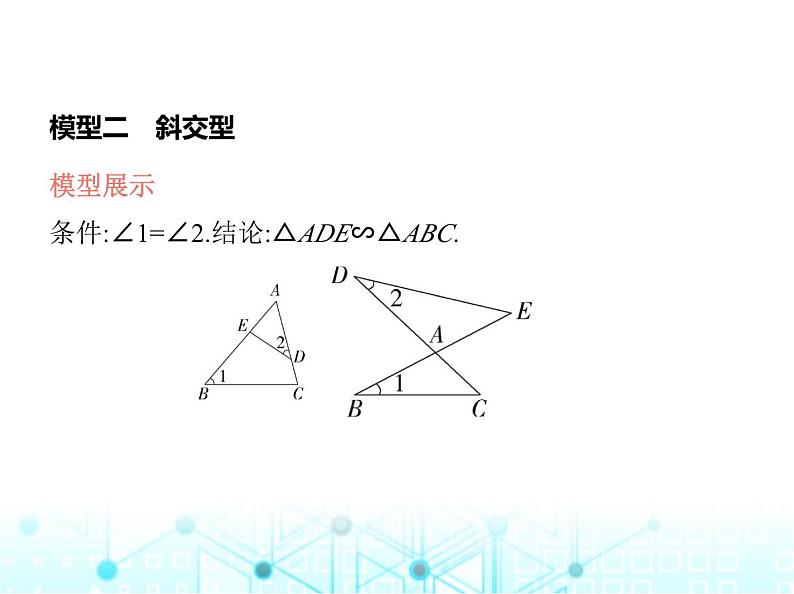
2.(2023广东揭阳中考)边长分别为10,6,4的三个正方形拼接 在一起,它们的底边在同一直线上(如图),则图中阴影部分的 面积为　　　    .
解析　∵三个四边形都是正方形,∴BF∥DE,∴△ABF∽△ ADE,∴ = ,∵AB=4,AD=4+6+10=20,DE=10,∴ = ,∴BF=2,∴GF=6-2=4,∵CK∥DE,∴△ACK∽△ADE,∴ = ,∵AC=4+6=10,AD=20,DE=10,∴ = ,∴CK=5,∴HK=6-5=1,∴阴影部分的面积= (HK+GF)·GH= ×(1+4)×6=15.
模型展示条件:∠1=∠2.结论:△ADE∽△ABC.      
3.(新考向·开放型试题)(2024湖南邵阳邵东月考)如图,已知AC、BD相交于点O,若补充一个条件后,便可得到△AOB∽△DOC,则要补充的条件可以是　　　　　     . 
答案不唯一,如∠A=∠D
解析　补充条件∠A=∠D时,∵∠AOB=∠COD,∠A=∠D,∴△AOB∽△DOC.
4.(2024河南驻马店汝南模拟)已知:在△ABC中,BD,CE分别 是AC,AB边上的高,连结ED,求证:△ABC∽△ADE. 
证明　设BD与CE交于点O,∵BD,CE分别是AC,AB边上的高, ∴∠BEC=∠BDC=90°,∵∠BOE=∠COD,∴∠ABD=∠ACE, ∵∠A=∠A,∴△ABD∽△ACE,∴ = ,∴ = ,∵∠A=∠A,∴△ABC∽△ADE.
模型展示条件:∠ACB=90°,CD⊥AB.结论:△ADC∽△ACB∽△CDB. 
5.(2023湖南湘潭中考)在Rt△ABC中,∠BAC=90°,AD是斜边 BC上的高.(1)证明:△ABD∽△CBA;(2)若AB=6,BC=10,求BD的长. 
解析    (1)证明:∵AD是斜边BC上的高,∴∠BDA=90°,∵∠ BAC=90°,∴∠BDA=∠BAC,∵∠B=∠B,∴△ABD∽△CBA.(2)由(1)知△ABD∽△CBA,∴ = ,∴ = ,∴BD=3.6.
模型四　一线三等角模型
模型展示(1)同侧型:如图1,已知∠A=∠CPD=∠B,当点P在线段AB上 时,易证△ACP∽△BPD.(2)异侧型:如图2,已知∠MAC=∠CPD=∠ABD,点P在线段AB 的延长线上时,易证△ACP∽△BPD.
6.(2023湖南邵阳中考)如图,CA⊥AD,ED⊥AD,点B是线段AD 上的一点,且CB⊥BE.已知AB=8,AC=6,DE=4.(1)证明:△ABC∽△DEB;(2)求线段BD的长. 
解析    (1)证明:∵CA⊥AD,ED⊥AD,CB⊥BE,∴∠A=∠CBE =∠D=90°,∴∠C+∠CBA=90°,∠CBA+∠DBE=90°,∴∠C= ∠DBE,∴△ABC∽△DEB.(2)∵△ABC∽△DEB,∴ = ,∴ = ,∴BD=3.
模型展示条件:∠A=∠A,∠ACD=∠B.结论:△ACD∽△ABC. 
7.(2024河南南阳南召期中)如图,△ABC中,AD是中线,BC=8, ∠B=∠DAC,求线段AC的长. 
解析　∵AD是中线,BC=8,∴BD=CD=4,在△CBA和△CAD 中,∵∠B=∠DAC,∠C=∠C,∴△CBA∽△CAD,∴ = ,∴AC2=CD·BC=4×8=32,∴AC=4 .
模型展示条件:DE∥BC,将△ADE旋转后,连结CE、BD.结论:(1)△ADE∽△ABC;(2)△ABD∽△ACE. 
8.(2023湖南常德中考改编)如图1,在Rt△ABC中,∠ABC=90°, AB=8,BC=6,D是AB上一点,且AD=2,过点D作DE∥BC交AC 于E,将△ADE绕A点顺时针旋转到图2的位置,求图2中 的值. 图1　     图2