华师大版九年级上册第23章 图形的相似23.3 相似三角形1. 相似三角形课堂教学课件ppt

这是一份华师大版九年级上册第23章 图形的相似23.3 相似三角形1. 相似三角形课堂教学课件ppt，共15页。PPT课件主要包含了成比例，对应边，对应角，知识回顾，对应练习1，知识探索，问题1，问题2，∴△ADE∽△ABC，知识概括等内容，欢迎下载使用。

1、两个边数相同的多边形,如果各边对应_________,各角对应_______,那么这两个多边形相似。
2、相似多边形的______________成比例，________相等。
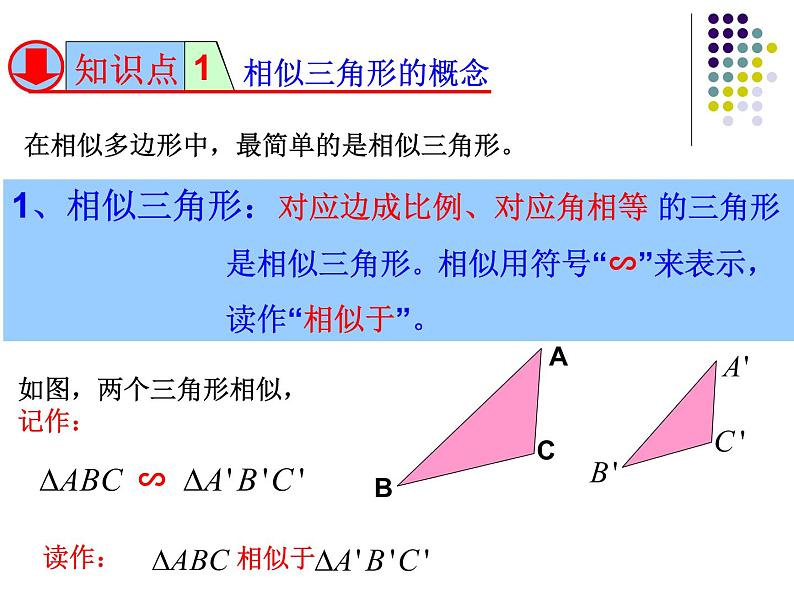
在相似多边形中，最简单的是相似三角形。
1、相似三角形：对应边成比例、对应角相等 的三角形 是相似三角形。相似用符号“∽”来表示， 读作“相似于”。
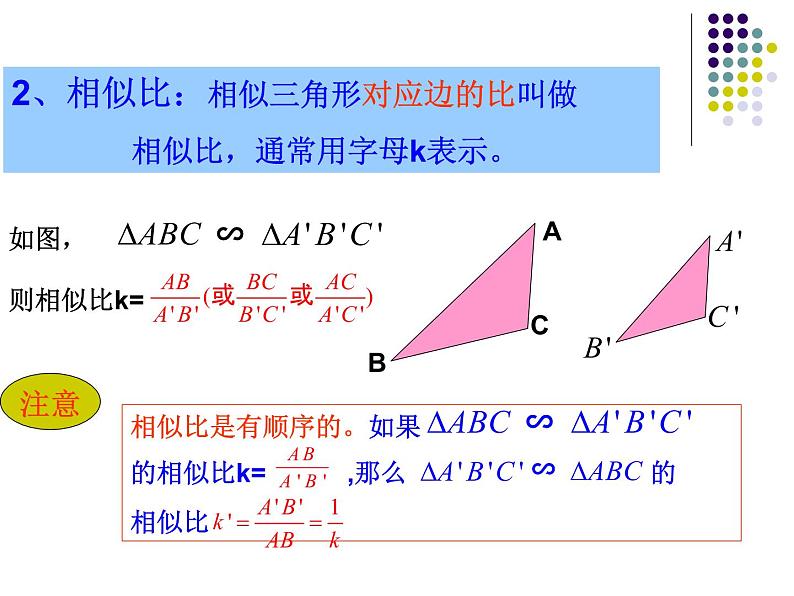
2、相似比：相似三角形对应边的比叫做 相似比，通常用字母k表示。
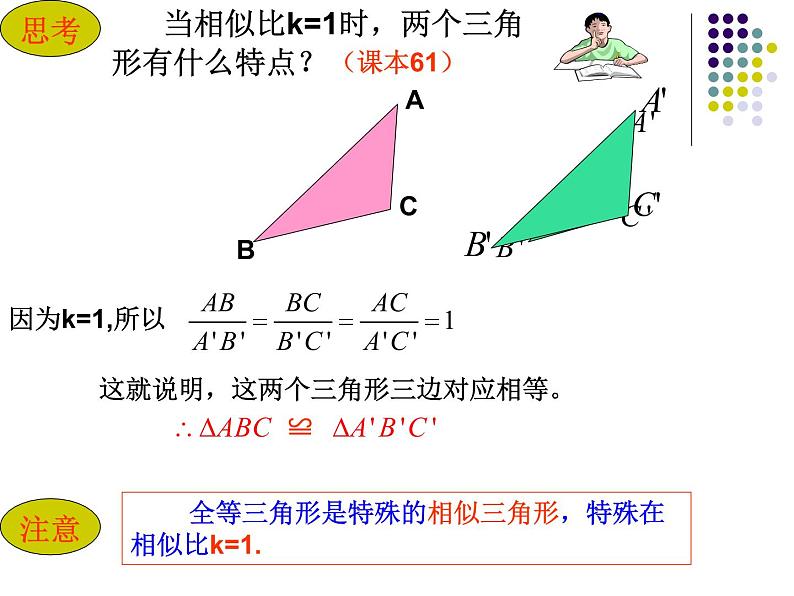
当相似比k=1时，两个三角形有什么特点？
这就说明，这两个三角形三边对应相等。
全等三角形是特殊的相似三角形，特殊在相似比k=1.
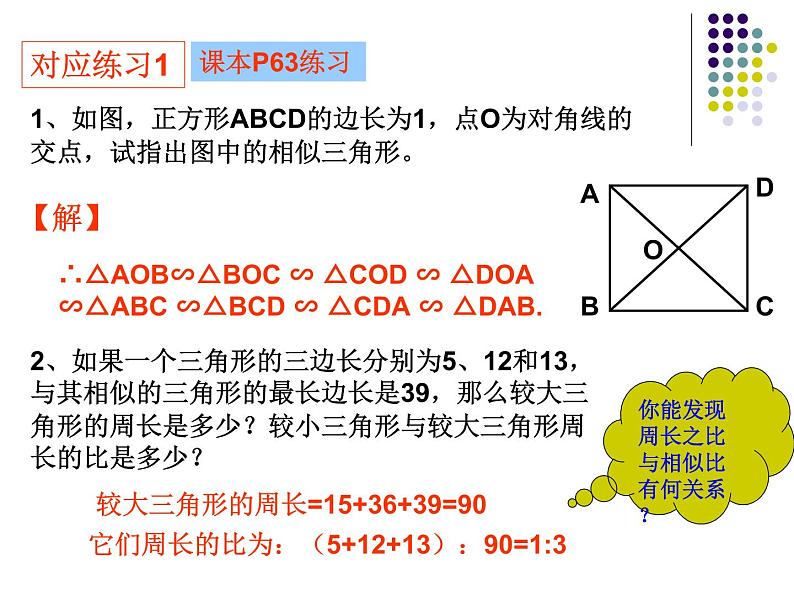
1、如图，正方形ABCD的边长为1，点O为对角线的交点，试指出图中的相似三角形。
∴△AOB∽△BOC ∽ △COD ∽ △DOA∽△ABC ∽△BCD ∽ △CDA ∽ △DAB.
2、如果一个三角形的三边长分别为5、12和13，与其相似的三角形的最长边长是39，那么较大三角形的周长是多少？较小三角形与较大三角形周长的比是多少？
你能发现周长之比与相似比有何关系？
较大三角形的周长=15+36+39=90
它们周长的比为：（5+12+13）：90=1:3
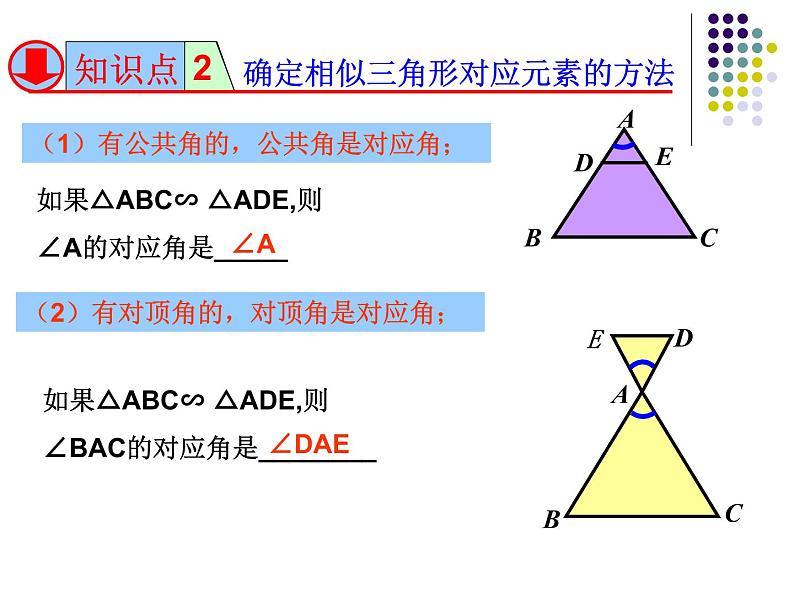
（1）有公共角的，公共角是对应角；
如果△ABC∽ △ADE,则∠A的对应角是_____
（2）有对顶角的，对顶角是对应角；
如果△ABC∽ △ADE,则∠BAC的对应角是________
（3）对应角所对的边是对应边，对应角所夹的边是对应边；
（4）对应边所对的角是对应角，对应边所夹的角是对应角；
如果AB对应DF,则∠C=______;
如图，DE∥BC, △ADE与△ABC是否相似？
要说明△ADE∽△ABC，根据定义，就要证明①对应角相等；②对应边成比例。
①在△ADE与△ABC中, ∠A=∠A,∵DE//BC,∴∠ADE=∠B, ∠AED=∠C.
②过点D作DF∥AC交BC于F点。
∵DE∥BC，∴DECF是平行四边形，∴CF=DE
而∠A=∠A,∠ADE=∠B, ∠AED=∠C.
如图，DE∥BC, △ADE与△ABC是否相似？
　　平行于三角形一边的直线，和其他两边（或两边的延长线）相交所构成的三角形与原三角形相似．
∵DE∥BC, ∴△ADE∽ △ABC
如图，在△ABC中，点D是边AB三等分点，DE∥BC,DE=5，求BC的长。
∴△ADE∽ △ABC（ ）
∵点D是边AB三等分点
如图，在△ABC中，点D是边AB四等分点，DE∥AC,DF ∥ BC,AC=8，BC=12. 求四边形DECF的周长。