2023-2024学年重庆市梁平区八年级（下）期末数学试卷（含解析）

这是一份2023-2024学年重庆市梁平区八年级（下）期末数学试卷（含解析），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.当a=5时，二次根式 4+a的值是( )
A. 3B. 2C. 1D. −1
2.下列正比例函数中，其图象恰好经过点(2,−4)的是( )
A. y=2xB. y=−2xC. y=12xD. y=−12x
3.如图，点O，B在数轴上所表示的数分别为0，3，CB⊥OB于点B，BC=2，以点O为圆心，OC长为半径画弧，交数轴于点A，若点A所表示的数为a，则a的值为( )
A. 13B. − 13C. 5D. − 5
4.“杂交水稻之父”袁隆平培育的超级杂交稻在全世界推广种植．某种植户为了考察所种植的杂交水稻苗的长势，从稻田中随机抽取7株水稻苗，测得苗高(单位：cm)分别是：23，24，23，25，26，23，25.则这组数据的众数和中位数分别是( )
A. 24，25B. 23，23C. 23，24D. 24，24
5.如图，在平面直角坐标系中，平行四边形ABCD的顶点A、B、C的坐标分别为(1,0)、(6,0)、(8,5)，则顶点D的坐标是( )
A. (5,5)
B. (5,3)
C. (2,5 )
D. (3,5)
6.已知最简二次根式 a+2与 18是同类二次根式，则a的值可能是( )
A. 16B. 0C. 2D. 任意实数
7.数学老师计算同学们一学期的总评成绩时，将平时、期中和期末的成绩按2：3：5计算，若小红平时、期中和期末的成绩分别是90分、85分、95分，则小红一学期的数学总评成绩是( )
A. 89分B. 91分C. 92分D. 93分
8.关于一次函数y=−x+6，下列结论正确的是( )
A. 图象不经过第二象限
B. 图象与x轴的交点是(0,6)
C. 图象与坐标轴形成的三角形的面积为36
D. 点(x1,y1)和(x2,y2)都在该函数图象上，若x1y2
9.如图，将一个长为20cm，宽为8cm的矩形纸片先按照从左向右对折，再按照从下向上的方向对折，沿所得矩形两邻边中点的连线(虚线)剪下(如图(1))，再打开，得到如图(2)所示的小菱形的面积为( )
A. 10cm2B. 20cm2C. 40cm2D. 80cm2
10.如图所示的是“顺风车”与“快车”的行驶里程x(千米)与计费y(元)之间的函数关系图象.有下列说法：①“快车”行驶里程不超过5千米计费8元；②“顺风车”行驶里程超过2千米的部分，每千米计费1.2元；③从甲地到乙地的路程是15千米，则“顺风车”要比“快车”多用3.4元；④点A的坐标是(6.5,10.4)，其中正确的个数为( )
A. 1
B. 2
C. 3
D. 4
二、填空题：本题共8小题，每小题4分，共32分。
11.计算 12× 13的结果是______．
12.摄氏温度用符号T表示，单位是℃(摄氏度)，华氏温度用符号F表示，单位是℉(华氏度).已知两种温度的换算公式为F=95T+32，则水的沸点100℃，换算成华氏温度为______℉.
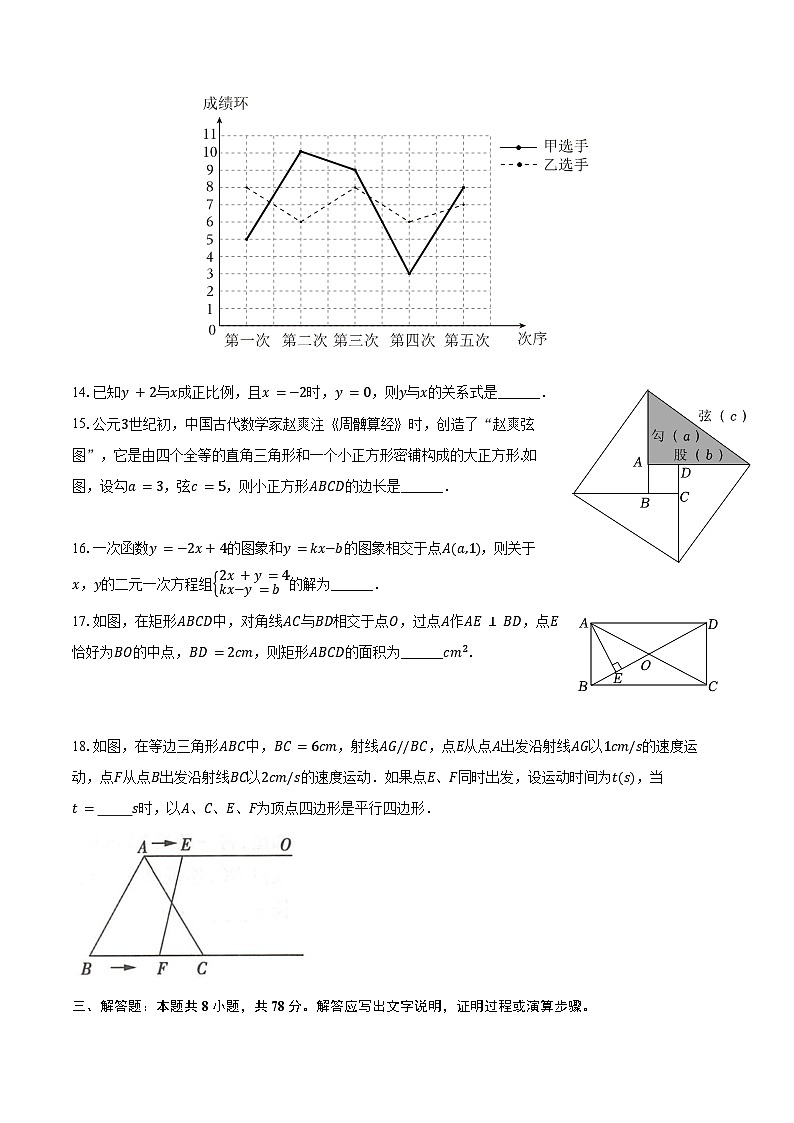
13.甲、乙两选手的射击成绩如图所示，方差分别记为S甲2，S乙2，则S甲2 ______S乙2.(填“>”“<”或“=”)
14.已知y+2与x成正比例，且x=−2时，y=0，则y与x的关系式是______．
15.公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”，它是由四个全等的直角三角形和一个小正方形密铺构成的大正方形.如图，设勾a=3，弦c=5，则小正方形ABCD的边长是______．
16.一次函数y=−2x+4的图象和y=kx−b的图象相交于点A(a,1)，则关于x，y的二元一次方程组2x+y=4kx−y=b的解为______．
17.如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，点E恰好为BO的中点，BD=2cm，则矩形ABCD的面积为______cm2．
18.如图，在等边三角形ABC中，BC=6cm，射线AG/​/BC，点E从点A出发沿射线AG以1cm/s的速度运动，点F从点B出发沿射线BC以2cm/s的速度运动．如果点E、F同时出发，设运动时间为t(s)，当t= s时，以A、C、E、F为顶点四边形是平行四边形．
三、解答题：本题共8小题，共78分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题8分)
计算：(1)3 3− 8−( 27− 2)3 3− 8−( 27− 2)；
(2)已知x= 5+ 7,y= 7− 5，求代数式x2+y2的值：
20.(本小题10分)
已知四边形ABCD是矩形，BD是对角线，过点C作CE⊥BD于点E，
(1)尺规作图：过点A作垂线AF，使得AF⊥BD于点F(不写作法)；
(2)连接AE、CF，求证：四边形AFCE是平行四边形．
∵四边形ABCD是矩形
∴ ______，AB/​/CD
∴∠ABF=∠CDE
∵CE⊥BD，AF⊥BD
∴ ______=90°
∴△ABF≌△CDE
∴ ______
又∵CE⊥BD，AF⊥BD
∴∠AFE=∠CEF=90°
∴ ______
∴四边形AFCE是平行四边形.(______的四边形是平行四边形)
21.(本小题10分)
如图，有一公路AB和一铁路CD在点A处交汇，且∠BAD=30°，在公路的点P处有一所学校(学校看作点P，点P与公路AB的距离忽略不计)，AP=320米，火车行驶时，火车周围200米以内会受到噪音的影响，现有一列动车在铁路CD上沿AD方向行驶，该动车车身长200米，动车的速度为180千米/时，那么在该动车行驶过程中．
(1)学校P是否会受到噪声的影响？说明理由；
(2)如果受噪声影响，那么学校P受影响的时间为多少秒？
22.(本小题10分)
2023年8月24日中午12点，日本福岛第一核电站启动核污染水排海，预估排放时间将长达30年.某学校为了解该校学生对此事件的关注与了解程度，对全校学生进行问卷测试，得分采用百分制，得分越高，则对事件的关注与了解程度就越高.现从七、八年级学生中各随机抽取20名学生的测试得分进行整理和分析(得分用x表示，单位：分，且得分为整数，共分为5组，A组：0≤x<60，B组：60≤x<70，C组：70≤x<80，D组：80≤x<90，E组：90≤x≤100)，下面给出了部分信息：
七年级被抽取的学生测试得分的所有数据为：48，62，79，95，88，70，88，55，74，87，88，93，66，90，74，86，63，68，84，82；
八年级被抽取的学生测试得分中，C组包含的所有数据为：72，77，78，79，75．
七、八年级被抽取的学生测试得分统计表
根据以上信息，解答下列问题：
(1)上述图表中：a= ______，b= ______；
(2)根据以上数据，你认为该校七、八年级学生在关注与了解日本核污染水排海事件上，哪个年级的学生对事件的关注与了解程度更高？请说明理由(一条理由即可)；
(3)若该校七年级有学生900人，八年级有学生800人，估计该校这两个年级的学生测试得分在C组的人数一共有多少人？
23.(本小题10分)
如图，分别以a，b，m，n为边长作正方形．
(1)若a=1,b= 2，求图1中两个正方形的面积之和；
(2)若m= 5,n= 3，求图2中AF的长；
(3)已知m>n且满足am−bn= 3，an+bm= 5，若图1中两个正方形的面积和为2，求图2中AF的长．
24.(本小题10分)
如表给出A，B，C三种宽带网的收费方式．
设上网时间为t小时，方案A、B、C的费用分别为y1、y2、y3．
(1)t=30时，求y1、y2的值.(直接写出结果)
(2)分别求出y1、y2、y3关于t的函数关系式，并注明变量t的取值范围．
(3)在同一坐标系中画出函数y1、y2、y3的图象，并选择出上网费用最低的收费方式．
25.(本小题10分)
在△ABC中，AB=AC，点D为射线BC上一动点(点D不与B，C重合)，以AD为边作菱形ADEF，使∠DAF=∠BAC，连接CF．
(1)如图1，当点D在线段BC上时，求证；BD=CF；
(2)如图2，当点D在线段BC的延长线上，且∠BAC=90°时，求证：BD=CF．
26.(本小题10分)
如图，直线y=−x+4与坐标轴分别交于点A，B，以OA为边在y轴的右侧作正方形AOBC．
(1)求点A，B的坐标；
(2)如图，点D是x轴上一动点，点E在AD的右侧，∠ADE=90°，AD=DE．
①探究发现，点E在一条定直线上，请直接写出该直线的解析式______；
②若点D是线段OB的中点，另一动点H在直线BE上，且∠HAC=∠BAD，请求出点H的坐标．
答案解析
1.【答案】A
【解析】解：当a=5时，二次根式 4+a= 4+5= 9=3，
故选：A．
2.【答案】B
【解析】解：A、把x=2代入y=2x得y=4≠−4，故函数y=2x不经过点(2,−4)，故A不符合题意；
B、把x=2代入y=−2x得y=4，故函数y=−2x经过点(2,−4)，故B符合题意；
C、把x=2代入y=2x得y=1≠−4，故函数y=12x不经过点(2,−4)，故C不符合题意；
D、把x=2代入y=−12x得y=−1≠−4，故函数y=−12x不经过点(2,−4)，故D不符合题意；
故选：B．
3.【答案】A
【解析】解：∵点O，B在数轴上所表示的数分别为0，3，
∴OB=3，
在Rt△BOC中，OC= OB2+BC2= 32+22= 13，
由作图可知，OA=OC= 13，
∴a的值为 13，
故选：A．
4.【答案】C
【解析】解：这组数据中，出现次数最多的是23，共出现3次，因此众数是23，
将这组数据从小到大排列，处在中间位置的一个数是24，因此中位数是24，
即：众数是23，中位数是24，
故选：C．
5.【答案】D
【解析】解：∵A、B、C的坐标分别为(1,0)、(6,0)、(8,5)，
∴D点纵坐标为：5，横坐标为：3，
故选：D．
6.【答案】B
【解析】解：∵ 18=3 2，
而最简二次根式 a+2与 18是同类二次根式，
∴a+2=2，
解得a=0．
故选：B．
7.【答案】B
【解析】解：小红一学期的数学总评成绩是90×2+85×3+95×52+3+5=91(分)，
故选：B．
8.【答案】D
【解析】解：A.∵k=−1<0，b=6>0，
∴一次函数y=−x+6的图象经过点一、二、四象限，
∴一次函数y=−x+6的图象不经过第三象限，选项A不符合题意；
B.当y=0时，−x+6=0，
解得：x=6，
∴一次函数y=−x+6的图象与x轴的交点是(6,0)，选项B不符合题意；
C.当x=0时，y=−1×0+6=6，
∴一次函数y=−x+6的图象与y轴的交点是(0,6)，
∴一次函数y=−x+6的图象与坐标轴形成的三角形的面积为12×6×6=18，选项C不符合题意；
D.∵k=−1<0，
∴y随x的增大而减小，
又∵点(x1,y1)和(x2,y2)都在该函数图象上，且x1∴y1>y2，选项D符合题意．
故选：D．
9.【答案】B
【解析】解：矩形对折两次后，所得的矩形的长、宽分别为原来的一半，即为10cm和4cm，
而沿两邻边中点的连线剪下，剪下的部分打开前相当于所得菱形的沿对角线两次对折的图形，
所以菱形的两条对角线的长分别为10cm，4cm，
所以S菱形=12×10×4=20(cm2).
故选：B．
10.【答案】D
【解析】解：①根据“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象可知：
行驶里程不超过5公里计费8元，即①正确；
②“滴滴顺风车”行驶里程超过2公里的部分，每公里计费为(14.6−5)÷(10−2)=1.2(元)，故②正确；
③令x=15，y1=1.6×15=24；令x=15，y2=1.2×15+2.6=20.6．
∴y1−y2=24−20.6=3.4(元)．
即甲、乙两地之间的里程是15公里，则“顺风车”要比“快车”少用3.4元，故③正确．
综上可知，正确的结论个数为4个．
④设x≥5时，“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系式为y1=k1x+b1，
将点(5,8)、(10,16)代入函数解析式得：
8=5k1+b116=10k1+b1，解得：k1=1.6b1=0．
∴“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系式为y1=1.6x；
当x≥2时，设“滴滴顺风车”的行驶里程x(公里)与计费y(元)之间的函数关系式为y2=k2x+b2，
将点(2,5)、(10,14.6)代入函数解析式得：
5=2k2+b214.6=10k2+b2，
解得：k2=1.2b2=2.6．
∴“滴滴顺风车”的行驶里程x(公里)与计费y(元)之间的函数关系式为y2=1.2x+2.6．
联立y1、y2得：y=1.6xy=1.2x+2.6，
解得：x=6.5y=10.4．
∴A点的坐标为(6.5,10.4)，故④正确；
故选：D．
11.【答案】2
【解析】解：原式= 12×13
= 4
=2．
故答案为：2．
12.【答案】212
【解析】解：将T=100代入F=95T+32，得F=95×100+32=212，
故答案为：212．
13.【答案】>
【解析】解：图表数据可知，
甲数据偏离平均数数据较大，乙数据偏离平均数数据较小，
即甲的波动性较大，即方差大，
故答案为：>．
14.【答案】y=−x−2
【解析】解：∵y+2与x成正比例(k≠0)，
∴设y+2=kx，
∵x=−2时，y=0，
∴2=−2k，解得k=−1，
∴y+2=−x，即y=−x−2．
故答案为：y=−x−2．
15.【答案】1
【解析】解：根据勾股定理可得b= c2−a2= 52−32=4，
∴小正方形ABCD的边长为4−3=1，
故答案为：1．
16.【答案】x=32y=1
【解析】解：∵一次函数y=−2x+4的图象和y=kx−b的图象相交于点A(a,1)，
∴1=−2a+4，
解得a=32，
∴A(32,1)，
∴二元一次方程组2x+y=4kx−y=b的解为x=32y=1，
故答案为：x=32y=1．
17.【答案】 3
【解析】解：∵四边形ABCD为矩形，
∴AC=BD，OB=OD=OA=OC，∠ABC=90°，
∵AE⊥BD，点E恰好为BO的中点，
∴AB=AO，
∴△ABO是等边三角形，
∴∠BAC=60°，∠ACB=30°
∴AB=12AC=12BD=1cm，BC= 3cm，
∴矩形ABCD的面积为BC⋅AB= 3×1= 3(cm2)；
故答案为： 3．
18.【答案】2或6
【解析】解：①当点F在C的左侧时，根据题意得：AE=tcm，BF=2tcm，
则CF=BC−BF=(6−2t)cm，
∵AG/​/BC，
∴当AE=CF时，四边形AECF是平行四边形，
即t=6−2t，解得：t=2；
②当点F在C的右侧时，根据题意得：AE=tcm，BF=2tcm，
则CF=BF−BC=(2t−6)cm，
∵AG/​/BC，
∴当AE=CF时，四边形AEFC是平行四边形，
即t=2t−6，解得：t=6．
综上可得：当t=2或6s时，以A、C、E、F为顶点四边形是平行四边形．
故答案为：2或6．
19.【答案】解：(1)原式=3 3−2 2−3 3+ 2，
=− 2；
(2)∵x= 5+ 7，y= 7− 5，
∴x+y=2 7，xy=2，
∴x2+y2=(x+y)2−2xy=(2 7)2−2×2=24．
【解析】(1)先化简二次根式，在和并同类项即可；
(2)先求出x+y=2 7，xy=2的值，代入计算即可．
20.【答案】AB=CD ∠AFB=∠CED AF=CE AF/​/CE 一组对边平行且相等
【解析】解：(1)以点A为圆心，适当长度为半径画弧，交对角线BD于点M、N，再分别以M、N为圆心，适当长度为半径画弧，交于点P，画射线AP，交对角线BD于点F，AF即为所求．
(2)连接AE、CF，求证：四边形AFCE是平行四边形．
∵四边形ABCD是矩形，
∴AB=CD，AB/​/CD，
∴∠ABF=∠CDE，
∵CE⊥BD，AF⊥BD，
∴∠AFB=∠CED=90°，
∴△ABF≌△CDE(AAS)，
∴AF=CE，
又∵CE⊥BD，AF⊥BD，
∴∠AFE=∠CEF=90°，
∴AF/​/CE，
∴四边形AFCE是平行四边形．(一组对边平行且相等的四边形是平行四边形)
故答案为：AB=CD，∠AFB=∠CED，AF=CE，AF/​/CE，一组对边平行且相等．
21.【答案】解：(1)如图作PH⊥CD于H．
在Rt△APH中，∵∠PAH=30°，PA=320m，
∴PH=12PA=160m，
∵160<200，
∴学校P会受到噪声的影响．
(2)当PE=PF=200时，动车在线段EF上时，受噪声影响，
∵EF=2FH= 2002−1602=240m，
180千米/时=50米/秒
∵240+20050=8.8秒，
答：学校P受影响的时间为8.8秒．
【解析】
(1)如图作PH⊥CD于H.求出PH与200比较即可；
(2)当PE=PF=200时，动车在线段EF上时，受噪声影响，求出EF的长即可解决问题；
22.【答案】88 25
【解析】解：(1)∵被抽取的学生测试得分的所有数据中，88出现3次是出现次数最多的数据，
∴a=88；
∵C组占比为：520×100%=25%，
∴b=25；
故答案为：88，25；
(2)七年级更高(答案不唯一)，理由如下：
因为七，八年级成绩的平均数相同，但七年级成绩的中位数80.(5分)大于八年级成绩的中位数77.(5分)，所以七年级的学生对事件的关注与了解程度更高；
(3)∵七年级处于C组的有4个数据，占比420×100%=20%，八处于C组的占比25%，
∴估计该校这两个年级的学生测试得分在C组的人数一共有20%×900+25%×800=380(人)，
答：估计该校这两个年级的学生测试得分在C组的人数一共有380人．
23.【答案】解：(1)S=a2+b2=12+( 2)2=3，
∴两个正方形的面积之和为3；
(2)由题意知，∠ACD=45°，∠GCF=45°，
∴∠ACF=∠ACD+∠GCF=90°，
由勾股定理得，AC2=m2+m2=( 5)2+( 5)2=10，CF2=n2+n2=( 3)2+( 3)2=6，
∴AF= AC2+CF2= 10+6=4；
∴AF的长为4；
(3)由题意知：a2+b2=2，
(3)∵am−bn= 3,an+bm= 5，
∴(am−bn)2=3①，(an+bm)2=5②，
①+②得，a2m2+b2n2−2abmn+a2n2+b2m2+2abmn=8，
整理得(a2+b2)(m2+n2)=8，
∴m2+n2=4；
在Rt△ACF中，AC= 2m，CF= 2n，
∴AF2=AC2+CF2=2(m2+n2)=2×4=8，
∴AF=2 2．
【解析】(1)根据正方形的面积公式直接求值即可；
(2)先确定∠ACF=90°，再由勾股定理求解即可；
(3)将已知的两个等式分别平方，求和后可求mn=1，再由△ACF是直角三角形，利用勾股定理解答即可．
24.【答案】解：(1)当t=30时，y1=30+(30−25)×60×0.05=45，y2=50，
∴y1的值为45，y2的值为50．
(2)当0≤t≤25时，y1=30；当t>25时，y1=30+(t−25)×60×0.05=3t−45，
∴y1关于t的函数关系式为y1=30(0≤t≤25)3t−45(t>25)．
当0≤t≤50时，y2=50；当t>50时，y2=50+(t−50)×60×0.05=3t−100，
∴y2关于t的函数关系式为y2=50(0≤t≤50)3t−100(t>50)．
y3关于t的函数关系式为y3=100(t≥0)．
(3)在同一坐标系中画出函数y1、y2、y3的图象如图所示：

当3t−45=50时，解得t=953(点P的横坐标)；
当3t−100=100时，解得t=2003(点Q的横坐标)．
由图象可知，当0≤t<953时，y1当t=953时，y1=y2当953当t=2003时，y2=y3当t>2003时，y3∴当0≤t<953时，选择A收费方式；
当t=953时，选择A收费方式或B收费方式均可；
当953当t=2003时，选择B收费方式或C收费方式均可；
当t>2003时，选择C收费方式．
【解析】(1)当t=30时，分别根据“A方案的费用=月使用费+(30−包时上网时间)×60×超时费”和“B方案的费用=月使用费”计算y1、y2的值即可；
(2)根据“当0≤t≤25时，A方案的费用=月使用费；当t>25时，A方案的费用=月使用费+(t−包时上网时间)×60×超时费”写出y1关于t的函数关系式并写成分段函数的形式；根据“当0≤t≤50时，B方案的费用=月使用费；当t>50时，B方案的费用=月使用费+(t−包时上网时间)×60×超时费”写出y2关于t的函数关系式并写成分段函数的形式；根据“C方案的费用=月使用费”写出y3关于t的函数关系式；
(3)根据(2)中求得的y1、y2、y3关于t的函数关系式，画出它们的图象，根据t的不同的取值范围比较y1、y2、y3的大小并选择函数值最小的方案即可．
25.【答案】证明：(1)∵四边形ADEF是菱形，
∴AD=AF，
∵∠BAC=∠DAF，
∴∠BAD=∠CAF，
∵AB=AC，
∴△BAD≌△CAF(SAS)，
∴BD=CF；
(2)四边形ADEF是菱形，
∴AD=AF，
∵∠BAC=∠DAF，
∴∠BAD=∠CAF，
∵AB=AC，
∴△BAD≌△CAF(SAS)，
∴BD=CF．
【解析】(1)根据四边形ADEF是菱形，则AD=AF，因为∠BAC=∠DAF，则∠BAD=∠CAF，证明△BAD≌△CAF(SAS)，推出BD=CF；
(2)四边形ADEF是菱形，则AD=AF，因为∠BAC=∠DAF，则∠BAD=∠CAF，证明△BAD≌△CAF(SAS)，推出BD=CF．
26.【答案】y=x−4
【解析】解：(1)把x=0代入y=−x+4，得y=4，
∴点A的坐标为(0,4)，
把y=0代入y=−x+4，得x=4，
∴点B的坐标为(4,0)；
(2)①过点E作EF⊥x轴，垂足为点F，
设点E的坐标为(x,y)，则OF=x，EF=y，
∵∠ADE=∠AOD=90°，
∴∠OAD+∠ADO=90°，∠FDE+∠ADO=90°，
∴∠OAD=∠FDE，
∵∠AOD=∠DFE=90°，AD=DE，
∴△AOD≌△DFE(AAS)，
∴OD=EF=y，OA=DF=4，
∵OF=OD+DF，
∴x=y+4，整理得y=x−4，
∴点E所在的直线的解析式为y=x−4；
②连接AE，由题意可知△ADE为等腰直角三角形，则∠DAE=45°，
∵四边形OACB为正方形，
∴∠BAC=∠DAE=45°，
∴∠EAC=∠BAD，此时点H与点E重合，
∵点D是线段OB的中点，
∴OD=BD=2，
∴点E的坐标为(6,2)，
设直线AE的解析式为y=kx+b，把A(0,4)，E(6,2)代入，
得6k+b=2b=4，解得k=−13b=4，
∴直线AE的解析式为y=−13x+4，
当x=4时，y=83，
∴点M的坐标为(4,83)，
作点M关于直线AC的对称点N，可得N(4,163)，
此时∠NAC=∠EAC=∠BAD，所以点H为直线AN与BE的交点，
∴直线AN的解析式为y=13x+4，
联立y=13x+4y=x−4，解得x=12y=8，
∴点H的坐标为(12,8)，
综上所述，点H的坐标为(6,2)或(12,8)．平均数
众数
中位数
七年级
77
a
80.5
八年级
77
89
77.5
收费方式
月使用费/元
包时上网时间/小时
超时费/(元/分钟)
A
30
25
0.05
B
50
50
0.05
C
100
不限时