初中17.3 勾股定理背景图课件ppt

这是一份初中17.3 勾股定理背景图课件ppt，共27页。PPT课件主要包含了知识点，勾股定理，一起探究，试着做做，b-a，几何语言，做一做，勾股定理与图形的面积等内容，欢迎下载使用。
1. 理解如何用面积法证明勾股定理，并掌握勾股定理的内容.2. 能用勾股定理进行简单的计算.3. 经历探索勾股定理的过程,发展合情推理的能力,体会数形结合的思想.
相传两千多年前，古希腊著名的哲学家、数学家毕达哥拉斯去朋友家做客. 在宴席上，其他的宾客都在尽情欢乐，只有毕达哥拉斯却看着朋友家地面所铺的瓷砖发起呆来. 原来，朋友家的地面是用一块块直角三角形形状的瓷砖铺成的，黑白相间，非常美观大方. 主人看到毕达哥拉斯的样子非常奇怪，就想过去问他，谁知，毕达哥拉斯突然恍然大悟的样子，站起来，大笑着跑着回家去了. 原来，他发现了瓷砖上的三个正方形存在着某种数学关系.
同学们，我们也来观察下面的图案，看看你能发现什么？
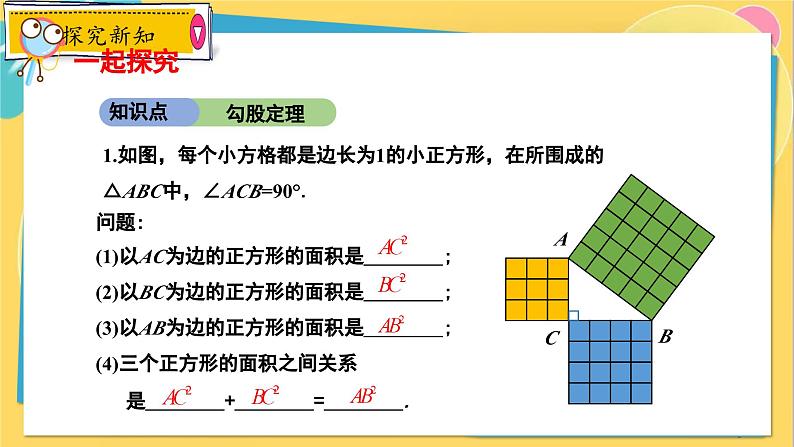
1.如图，每个小方格都是边长为1的小正方形，在所围成的△ABC中，∠ACB=90°.
问题:(1)以AC为边的正方形的面积是　　　　; (2)以BC为边的正方形的面积是　　　　; (3)以AB为边的正方形的面积是　　　　; (4)三个正方形的面积之间关系 是　　　　+　　　　=　　　　. 
刚才我们接触到的是一般的直角三角形,那么对于等腰直角三角形是否也存在这个关系呢?
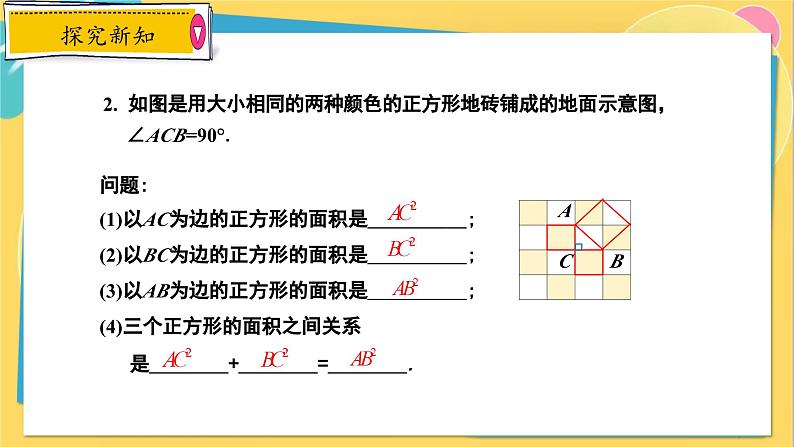
2. 如图是用大小相同的两种颜色的正方形地砖铺成的地面示意图，∠ACB=90°.
问题:(1)以AC为边的正方形的面积是　　　　　; (2)以BC为边的正方形的面积是　　　　　; (3)以AB为边的正方形的面积是　　　　　; (4)三个正方形的面积之间关系 是　　　　+　　　　=　　　　. 
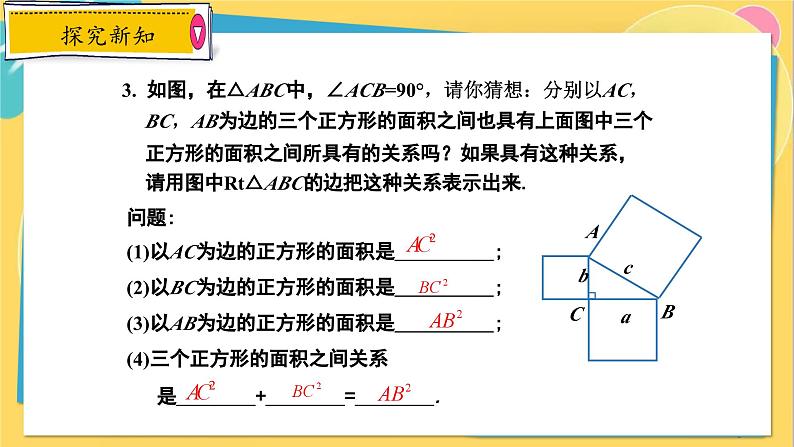
3. 如图，在△ABC中，∠ACB=90°，请你猜想：分别以AC，BC，AB为边的三个正方形的面积之间也具有上面图中三个正方形的面积之间所具有的关系吗？如果具有这种关系，请用图中Rt△ABC的边把这种关系表示出来.
通过探究可知：在直角三角形中，两条直角边的平方和等于斜边的平方.
如图是用四个全等的直角三角形拼成的，其中，四边形ABDE和四边形CFGH都是正方形.请你根据此图，利用它们之间的面积关系推导出：a2 +b2=c2.
∵ S大正方形＝c2，
S小正方形＝(b-a)2，
∴ S大正方形＝4·S三角形＋S小正方形，
如图，我国古代把直角三角形较短的直角边叫做“勾”，较长的直角边叫做“股”，斜边叫做“弦”.因此，直角三角形三边之间的关系称为勾股定理 .
勾股定理：如果直角三角形两直角边分别为a，b，斜边为c，那么a2+b2=c2.
勾股定理也可叙述为：直角三角形两直角边的平方和等于斜边的平方.
∵在Rt△ABC中，∠C=90°，
∴a2+b2=c2（勾股定理）.
勾股定理揭示了直角三角形三边之间的关系.
a2 + b2 = c2
a2 = c2－b2
b2 = c2－a2
在直角三角形中，如果知道两条边的长，根据勾股定理，可求出第三边的长.
请比较图(1)和图(2)中两个正方形的面积，验证勾股定理.
由图(1)可知大正方形的边长为：a+b，则面积为(a+b)2，图中把大正方形的面积分为了4部分，分别是：边长为a的正方形，边长为b的正方形，还有两个长为b，宽为a的长方形，根据面积相等得： ∴a2+b2=c2，所以勾股定理成立.
由图(2)可知大正方形的边长为：a+b，则面积为(a+b)2，图中把大正方形的面积分为了5部分，分别是：边长为c的正方形，还有4个相等的直角三角形，根据面积相等得：∴a2+b2=c2，所以勾股定理成立.
如图所示，等腰三角形ABC中，AB=AC ，AD是底边上的高，若AB=5 cm，BC=6 cm，则AD= cm．
分析：本题考查了等腰三角形三线合一的性质，即等腰三角形底边上的中线，底边上的高重合，利用三线合一的性质求得线段的长度后，再利用勾股定理求出AD边的长度.
1 .下列说法中正确的是(　　) A．已知a，b，c是三角形的三边，则a2＋b2＝c2 B．在直角三角形中，两边的平方和等于第三边的平方 C．在Rt△ABC中，∠C＝90°，则a2＋b2＝c2 D．在Rt△ABC中，∠B＝90°，则a2＋b2＝c2
2.在Rt△ABC中，∠C=90°，AC=9，BC=12，则 点C到AB的距离是(　　) A. B. C. D.
在直角三角形中应用勾股定理求边长时，要分清斜边和直角边，避免盲目代入勾股定理的公式.
如图所示，在△ABC中，∠ACB=90°，以△ABC的各边为边在△ABC外作三个正方形，S1，S2 ，S3分别表示这三个正方形的面积，S1=81，S3=225，则S2=______．
解：由勾股定理，得AC2+BC2=AB2 .又∵S1=AC2， S2=BC2，S3=AB2 ，∴S1+S2=S3. 即S2=S3－S1=225—81=144. 故填144.
1.如图所示，分别以Rt△ABC的三边为边向外作正方形，其面积分别为S1、S2、S3，且S1=4，S2=8．试求S3.
解：在Rt△ABC中，由勾股定理得BC2+AC2=AB2． 所以S3=AB2=BC2+AC2=S1+S2=12．
解析：把正方形的面积用边长的平方表示，然后利用勾股定理求解．
2.如图，已知△ABC为直角三角形，分别以直角边AC、BC为直径作半圆AmC和BnC，以AB为直径作半圆ACB，记两个月牙形阴影部分的面积之和为S1，△ABC的面积为S2，则S1与S2的大小关系为(　　) A．S1＞S2 B．S1＜S2 C．S1＝S2 D．不能确定
1. 在△ ABC 中，∠ C ＝90°，∠ A ，∠ B ，∠ C 的对边分 别是 a ， b ， c ，则下列式子成立的是(　A　)
∵∠ C ＝90°，∠ A ，∠ B ，∠ C 的对边分别是 a ， b ， c ，∴ a2＋ b2＝ c2.故选A.
3. [2023·随州]如图，在Rt△ ABC 中，∠ C ＝90°， AC ＝ 8， BC ＝6， D 为 AC 上一点，若 BD 是∠ ABC 的平分 线，则 AD ＝ ⁠.