吉林省长春市朝阳区2023-2024学年八年级下学期期末数学试题

这是一份吉林省长春市朝阳区2023-2024学年八年级下学期期末数学试题，共9页。试卷主要包含了计算等内容，欢迎下载使用。

1.答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内.
2.答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试卷上答题无效。
一、选择题（每小题3分，共24分）
1.若分式的值为0，则x的值是
A.0B.6C.-3D.-6
2.2024年5月中旬，长春牡丹园的牡丹花竟相开放，国色天香.某品种的牡丹花粉直径约为0.000354米，则数据0.000354用科学记数法表示为
A.B.C.D.
3.在平面直角坐标系中，反比例函数的图象一定经过的点是
A.（3，-4）B.（-4，3）C.（-2，-6）D.（2，-6）
4.某鞋店试销一种新款女鞋，试销期间卖出的情况如下表.
若这个鞋店的经理想知道哪种型号的鞋最杨销，则下列统计量对鞋店的经理来说最有意义的是
A.平均数B.方差C.中位数D.众数
5.在平面直角坐标系中，若将直线向上平移2个单位长度得到直线，则直线对应的函数关系为
A.B.C.D.
6.如图，将两张对边平行的纸条交叉叠放在一起，重合部分构成一个四边形ABCD，转动一张纸条的过程中，下列结论：①四边形ABCD的周长不变；②四边形ABCD的面积有变化；③；④；其中一定正确的是
A.②④B.①③C.①②D.②③
7.如图，在矩形ABCD中，AB=6，BC=8，对角线AC、BD相交于点O.将沿着射线AD的方向平移线段AD的长度得到，点A、O的对应点分别为点D、E.则四边形OCED的周长为
A.20B.16C.10D.8
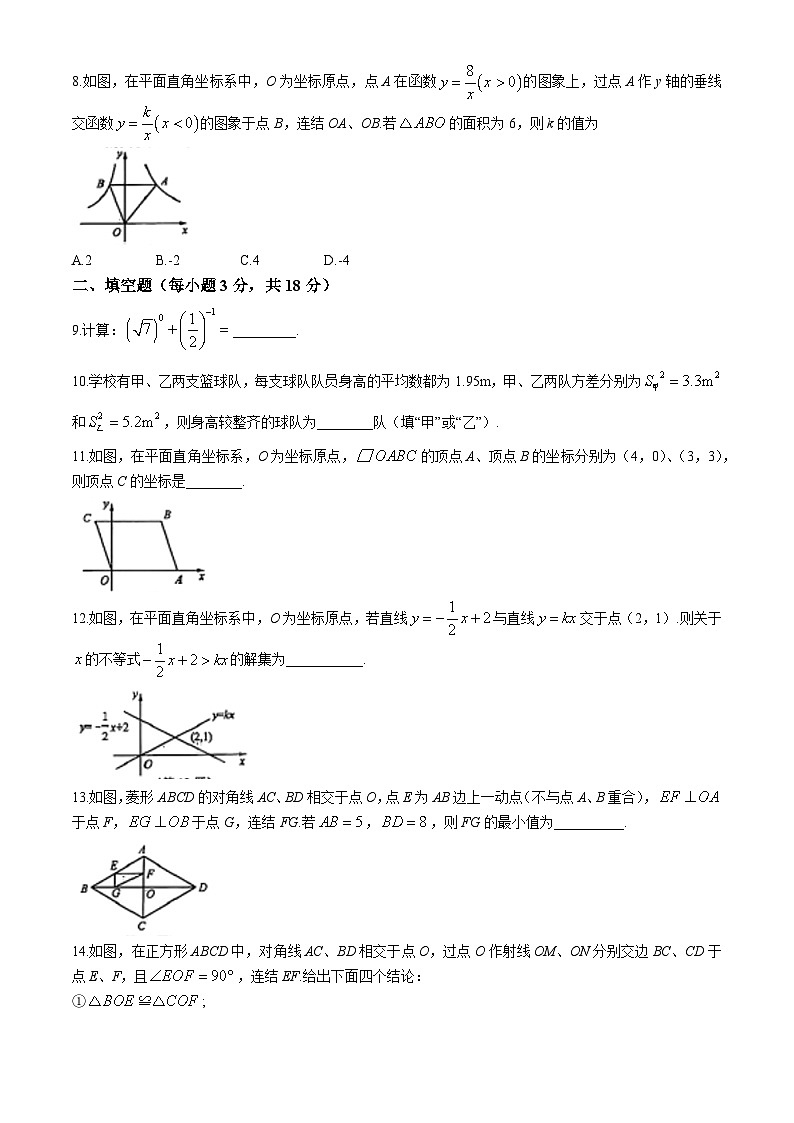
8.如图，在平面直角坐标系中，O为坐标原点，点A在函数的图象上，过点A作y轴的垂线交函数的图象于点B，连结OA、OB.若的面积为6，则k的值为
A.2B.-2C.4D.-4
二、填空题（每小题3分，共18分）
9.计算：_________.
10.学校有甲、乙两支篮球队，每支球队队员身高的平均数都为1.95m，甲、乙两队方差分别为和，则身高较整齐的球队为________队（填“甲”或“乙”）.
11.如图，在平面直角坐标系，O为坐标原点，的顶点A、顶点B的坐标分别为（4，0）、（3，3），则顶点C的坐标是________.
12.如图，在平面直角坐标系中，O为坐标原点，若直线与直线交于点（2，1）.则关于的不等式的解集为___________.
13.如图，菱形ABCD的对角线AC、BD相交于点O，点E为AB边上一动点（不与点A、B重合），于点F，于点G，连结FG.若，，则FG的最小值为__________.
14.如图，在正方形ABCD中，对角线AC、BD相交于点O，过点O作射线OM、ON分别交边BC、CD于点E、F，且，连结EF.给出下面四个结论：
①;
②;
③四边形CEOF的面积为正方形ABCD面积的;
④.
上述结论中，所有正确的序号是__________.
三、解答题（本大题10小题，共78分）
15.（6分）先化简，再求值：，其中.
16.（6分）已知y与x成正比例，且当时，.
（1）求y与x之间的函数关系式.
（2）若点在此函数图象上，求a的值.
17.（6分）某中学在“五·四”青年节来临之际，购进A、B两种运动衫共88件，已知购买A、B两种运动衫的费用都是2400元，A种运动衫的单价是B种运动衫单价的1.2倍.求B种运动衫的单价.
18.（7分）图①、图②、图③均是5×5的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点叫格点.图①、图②、图③中线段AB的端点均在格点上，在图①、图②、图③中分别以AB为对角线画一个四边形ACBD，使该四边形的顶点均在格点上，只用无刻度的直尺，在给定的网格中，分别按下列要求画图，并保留作图痕迹。
（1）在图①中画矩形ACBD，使其面积为3.
（2）在图②中画正方形ACBD.
（3）在图③中画，使其面积为10.
19.（7分）如图，在四边形ABCD中，，，AC平分，连结BD交AC于D点O，过点C作交AB延长线于点E.
（1）求证：四边形ABCD为菱形.
（2）若，，则CE的长为________.
20.（7分）小刚在今年的全校篮球联赛中表现优异，下表是他在这场联赛中，分别与甲队和乙队各四场比赛中的得分统计（其中得分、篮板、失误的单位均是分）.
（1）小刚在对阵甲队时的平均每场得分a的值是__________.
（2）小刚在这8场比赛的篮板统计中，众数是_________分，中位数是_________分.
（3）如果规定综合得分为：平均每场得分×1+平均每场篮板×1.2+平均每场失误×（-1），且综合得分越高表现越好，通过计算说明小刚在对阵哪一个队时表现更好。.
21.（8分）如图，在平面直角坐标系中，O为坐标原点，矩形OABC的顶点在反比例函数的图象上，轴于点A.点D为边AB中点，过点D作交该函数图象于点E，过点E作轴于点F，过点E的正比例函数的图象与该函数的另一个交点为点G.
（1）_________.
（2）求点E的坐标及四边形ADEF的面积.
（3）当正比例函数的值大于反比例函数的值时，直接写出x的取值范围.
22.（9分）【感知】如图①，在矩形ABCD中，，.P为射线BC上一点，将沿直线AP翻折得到，点B的对称点为点.若点在边AD上，则PD的长为________.
【探究】如图②，图①中的点在矩形ABCD的内部，点在直线PD上，其它条件不变.
（1）求证：.
（2）BP的长为________.
【应用】如图③，当图①中的点P在BC延长线上，且点在直线PD上时，其它条件不变.直接写出四边形的面积.
23.（10分）某品牌烤箱新增一种安全烤制模式，在此模式下烤箱内温度匀速升至240℃时烤箱停止加热，随后烤箱内温度下降至初始温度，该品牌烤箱安全烤制模式下烤箱内温度y（℃）与加热时间x（min）之间的函数图象如图所示.
（1）直接写出该品牌烤箱的烤箱内温度匀速上升期间y与x之间的函数表达式，并写出自变量x的取值范围.
（2）求该品牌烤箱的烤箱内温度匀速下降期间y与x之间的函数表达式。并写出自变量x的取值范围.
（3）若食物在130℃及以上的温度中烤制6分钟以上才可健康食用，该模式下烤制的食物能否健康食用?并说明理由.
24.（12分）如图，矩形ABCD中，，，点P、点Q分别在边AB、CD上，且.
连结AQ、DP相交于点M，连结CP、BQ相交于点M.
（1）当时，大小为________度.
（2）求证：四边形PMQN是平行四边形.
（3）当时，求证：四边形PMQN是矩形
（4）在不添加辅助线与字母的前提下，若图中存在菱形，直接写由该菱形的边长；若不存在，请说明理由.
2023—2024学年度（下学期）期末质量监测试题八年级数学答案
阅卷说明：
1.评卷采分最小单位为1分，每步标出的是累计分.
2.考生若用本“参考答案”以外的解（证）法，可参照本“参考答案”的相应步骤给分.
一、选择题（每小题3分，共24分）
1.B 2.A 3.C 4.D 5.B 6.D 7.A 8.D
二、填空题（每小题3分，共18分）
9.3 10.甲 11.（-1，3） 12. 13. 14.①②③
三、解答题（本大题10小题，共78分）
15.原式.
当时，原式.
16.（1）设.
把当时，代入，得.
即.
∴y与x之间的函数关系式为.
（2）把点代入，得.
解得.
17.设B种运动衫单价是x元.
由题意，得.
解得.
经检验，是所列方程的解，且符合题意，
答：B种运动衫的单价是50元.
18.以下答案供参考.
（1）如图①.
（2）如图②.
（3）如图③.评分说明：三个小题不标字母均得分；不用直尺画可得分，面成虚线可得分.
19.（1）（1）∵，，
∴，且四边形ABCD是平行四边形，
∵AC平分，∴.∴.∴.
∴是菱形.
（2）
20.（1）25
（2）10 11
（3）小刚在对阵甲队时的综合得分为25X1+11×12+3×（-1）=35.2（分）.
对阵乙队时的综合得分为18.5×1+13×1.2+2×（-1）=32.1（分）.
∵35.2>32.1，
∴小刚在对阵甲队时表现更好.
21.（1）8
（2）∵D为边AB中点，点，
∴点D的坐标为（2，2）.
当时，.
解得.
∴点E坐标为（4，2）
∴.
∴四边形ADEF的面积为4.
（3）根据图象正比例函数值大于反比例函数值的x的取值范围为或.
22.【感知】
【探究】（1）∵四边形ABCD是矩形，
∴，，
∴.
由翻折，得，.
∴，.
∴.
（2）2
【应用】32
【探究】第（1）题采用其它方法可参照此评分标准.
23.（1）该品牌烤箱的烤箱内温度匀速上升期间y与的函数关系式为.
（2）设该品牌烤箱的烤箱内温度匀速下降期间y与之间的函数关系为.
由题意，得
解得
∴该品牌烤箱的烤箱内温度匀速下降期间y与x的函数关系式为.
（3）当时，令，则.
解得.
当时，令，则，
解得.
∵12.5-5=7.5>6，
∴该模式下烤制的食物能健康食用.
24.（1）90
（1分）
（2）∵四边形ABCD是矩形，
∴，，∴.
∵，∴四边形APCQ是平行四边形.
∴.
∵，∴.
∵，∴四边形BPDQ是平行四边形.
∴.
∴四边形PMQN是平行四边形.
（3）如图①，.
∵四边形ABCD是矩形
∴，，.
由勾股定理，得.
∴.同理.
∴.
∵，∴.
∴是直角三角形.
∴.
∴平行四边形PMQN是矩形.
（4）当四边形BPDQ或四边形APCQ是菱形时，其边长为5.8.
当四边形PMQN是菱形时，其边长为.
【提示】如图②、图③、图④.
型号
22
22.5
23
23.5
24
24.5
25
数量/双
3
5
10
15
8
3
2
场次
对阵甲队
对阵乙队
得分
篮板
失误
得分
篮板
失误
第一场
21
10
2
25
17
2
第二场
29
10
2
31
15
0
第三场
24
14
3
16
12
4
第四场
26
10
5
2
8
2
平均值
11
3
18.5
13
2