资料中包含下列文件,点击文件名可预览资料内容


















还剩23页未读,
继续阅读
所属成套资源:苏科版数学九下课件PPT+分层练习全册
成套系列资料,整套一键下载
初中数学苏科版九年级下册7.2 正弦、余弦优质ppt课件
展开
这是一份初中数学苏科版九年级下册7.2 正弦、余弦优质ppt课件,文件包含苏科版数学九年级下册721《正弦余弦》第1课时同步课件pptx、苏科版数学九年级下册722《正弦余弦》第2课时同步课件pptx、苏科版数学九年级下册72《正弦余弦》五大题型原卷版docx、苏科版数学九年级下册72《正弦余弦》五大题型解析版docx等4份课件配套教学资源,其中PPT共63页, 欢迎下载使用。
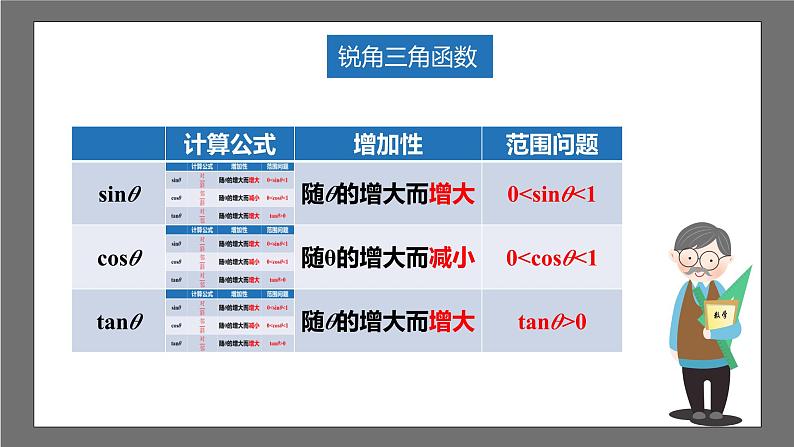
理解锐角三角函数的概念及增减性
掌握同角三角函数的基本关系式
理解互余的两个锐角的三角函数值之间的关系
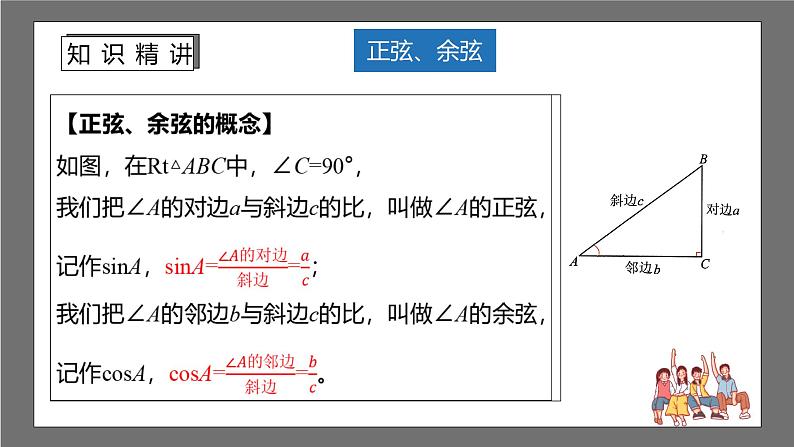
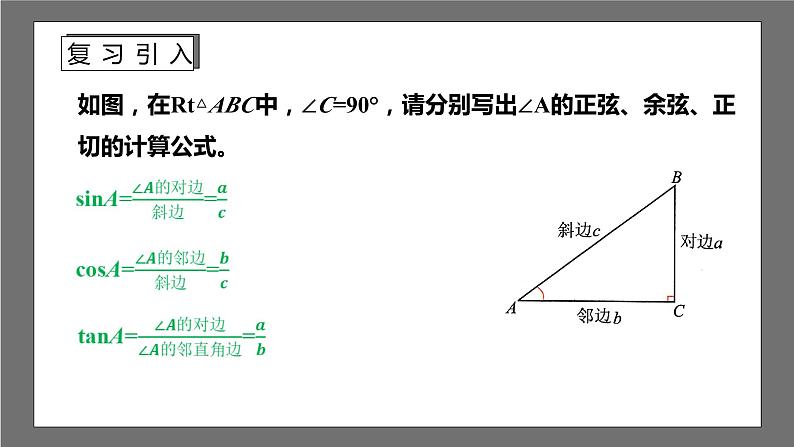
如图,在Rt△ABC中,∠C=90°,请分别写出∠A的正弦、余弦、正切的计算公式。
例1、在直角三角形中,若各边都扩大为原来的2倍,则其锐角的三角函数值( )A.都扩大为原来的2倍B.都缩小为原来的一半C.都没有变化D.不能确定
【分析】锐角的三角函数值只与∠A的大小有关,与直角▲的边长无关(我们只是利用边长计算数值而已)
同角三角函数的基本关系式
将下列表格填完整,你发现了什么?
证明1:如图,证明:sin2A+cs2A=1
【区分sin2A、sinA2与sin2A】sin2A=sinA·sinAsinA2表示A2的正弦sin2A表示2A的正弦(同样适用于余弦、正切)
例3、x为锐角,且tanx=2,那么sinx=________,csx=________。
已知锐角三角函数中的其中一个值,即可求出另外两个值(简称“知一求二”)法一:公式法——同角三角函数的基本关系式;法二:数形结合——画直角三角形。
互余的两个锐角的三角函数值之间的关系
根据表格完成下列填空,你发现了什么?(1)sin30°________cs60°,sin45°________cs45°,sin60°________cs30°;(填“<”、“=”或“>”)(2)tan30°·tan60°=________,tan45°·tan45°=________。
证明1:如图,证明:sinA=cs(90°-A),csA=sin(90°-A)
证明2:如图,证明:tanA·tan(90°-A)=1
【互余的两个锐角的三角函数值之间的关系】(1)sinA=cs(90°-A),csA=sin(90°-A);(2)tanA·tan(90°-A)=1。
例2、用不等号“>”或“<”连接:sin50°________cs50°。
【分析】∵cs50°=sin40°,sin50°>sin40°,∴sin50°>cs50°。
【总结】比较非特殊角的三角函数值时,必须先转化成同一三角函数,再根据增减性比较大小。
【分析】∵sin36°=cs54°,tan20°·tan70°=1,∴原式=1+2=3。
理解锐角三角函数的概念及增减性
掌握同角三角函数的基本关系式
理解互余的两个锐角的三角函数值之间的关系
如图,在Rt△ABC中,∠C=90°,请分别写出∠A的正弦、余弦、正切的计算公式。
例1、在直角三角形中,若各边都扩大为原来的2倍,则其锐角的三角函数值( )A.都扩大为原来的2倍B.都缩小为原来的一半C.都没有变化D.不能确定
【分析】锐角的三角函数值只与∠A的大小有关,与直角▲的边长无关(我们只是利用边长计算数值而已)
同角三角函数的基本关系式
将下列表格填完整,你发现了什么?
证明1:如图,证明:sin2A+cs2A=1
【区分sin2A、sinA2与sin2A】sin2A=sinA·sinAsinA2表示A2的正弦sin2A表示2A的正弦(同样适用于余弦、正切)
例3、x为锐角,且tanx=2,那么sinx=________,csx=________。
已知锐角三角函数中的其中一个值,即可求出另外两个值(简称“知一求二”)法一:公式法——同角三角函数的基本关系式;法二:数形结合——画直角三角形。
互余的两个锐角的三角函数值之间的关系
根据表格完成下列填空,你发现了什么?(1)sin30°________cs60°,sin45°________cs45°,sin60°________cs30°;(填“<”、“=”或“>”)(2)tan30°·tan60°=________,tan45°·tan45°=________。
证明1:如图,证明:sinA=cs(90°-A),csA=sin(90°-A)
证明2:如图,证明:tanA·tan(90°-A)=1
【互余的两个锐角的三角函数值之间的关系】(1)sinA=cs(90°-A),csA=sin(90°-A);(2)tanA·tan(90°-A)=1。
例2、用不等号“>”或“<”连接:sin50°________cs50°。
【分析】∵cs50°=sin40°,sin50°>sin40°,∴sin50°>cs50°。
【总结】比较非特殊角的三角函数值时,必须先转化成同一三角函数,再根据增减性比较大小。
【分析】∵sin36°=cs54°,tan20°·tan70°=1,∴原式=1+2=3。













