+山东省青岛市即墨区2023-2024学年八年级下学期7月期末联考数学试题
展开(考试时间: 120分钟 满分: 120分)
友情提示。亲爱的同学,欢迎你参加本次考试,祝你答题成功!
本试题共25道题.第1—10题为选择题,共30分; 第11—16题为填空题,共18分;第17—25题为解答题,共72分.要求所有题目均在答题卡上作答,在本卷上作答无效.
第Ⅰ卷(共30分)
一、选择题(本题满分30分,共有10道小题,每小题3分)
下列每小题都给出标号为A、B、C、D的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.
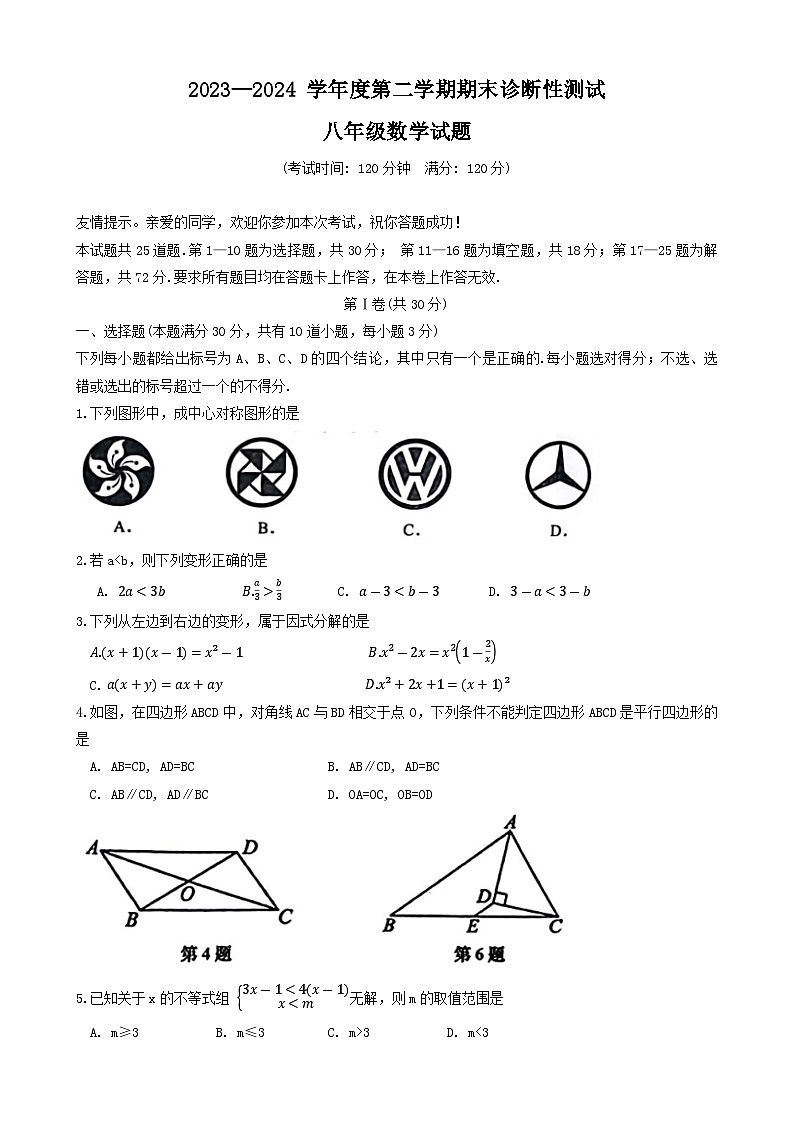
1.下列图形中,成中心对称图形的是
2.若a
A.x+1x-1=x²-1 B.x2-2x=x21-2x
C. a(x+y)=ax+ay D.x²+2x+1=x+1²
4.如图,在四边形ABCD中,对角线AC与BD相交于点 O,下列条件不能判定四边形ABCD是平行四边形的是
A. AB=CD, AD=BC B. AB∥CD, AD=BC
C. AB∥CD, AD∥BC D. OA=OC, OB=OD
5.已知关于x的不等式组 3x-1<4x-1x
6. 如图,△ABC中, AB=6cm, AC=4cm,点E是BC的中点, 若AD平分∠BAC, CD⊥AD,线段DE的长为
A. 0.5cm B. 1cm C. 1.5cm D. 2cm
7.如果关于x的分式方程 mx-2+2xx-2=1有增根,那么m的值为
A. -2 B. 2 C. 4 D. -4
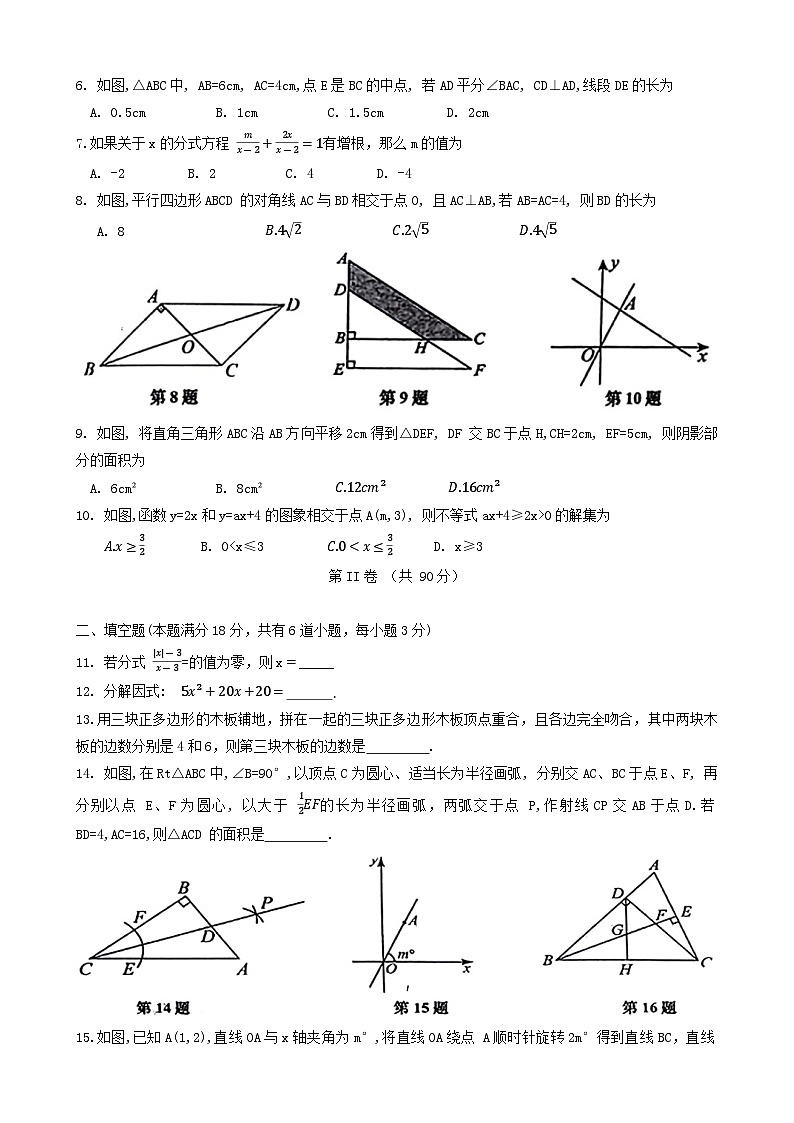
8. 如图,平行四边形ABCD 的对角线AC与BD相交于点O, 且AC⊥AB,若AB=AC=4, 则BD的长为
A. 8 B.42 C.25 D.45
9. 如图, 将直角三角形ABC沿AB方向平移2cm得到△DEF, DF 交BC于点H,CH=2cm, EF=5cm, 则阴影部分的面积为
A. 6cm² B. 8cm² C.12cm² D.16cm²
10. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3), 则不等式ax+4≥2x>0的解集为
A.x≥32 B. 0
二、填空题(本题满分18分,共有6道小题,每小题3分)
11. 若分式 |x|-3x-3=的值为零,则 x=_____
12. 分解因式: 5x²+20x+20= .
13.用三块正多边形的木板铺地,拼在一起的三块正多边形木板顶点重合,且各边完全吻合,其中两块木板的边数分别是4和6,则第三块木板的边数是 .
14. 如图,在Rt△ABC中,∠B=90°,以顶点C为圆心、适当长为半径画弧, 分别交AC、BC于点E、F, 再分别以点 E、F为圆心, 以大于 12EF的长为半径画弧,两弧交于点 P,作射线CP交AB于点D.若BD=4,AC=16,则△ACD 的面积是 .
15.如图,已知A(1,2),直线OA与x轴夹角为m°,将直线OA绕点 A顺时针旋转2m°得到直线BC,直线BC与x轴交于B,与y轴交于C,则 SAOnSAOC= ¯.
16.如图,在△ABC中,∠ABC=45°,CD⊥AB于点 D,BE平分∠ABC,且BE⊥AC于点E,BE与CD相交于点 F, BF=2CE,H是BC边的中点,连接DH 与BE 相交于点 G,下列结论正确的有 . (填写正确结论的序号)
①∠A=67.5°; ②DF =AD; ③DH⊥BC; ④BE=2BG
三、解答题(本题满分72分)
17. (本题满分4分) 如图,在Rt△ABC中, ∠A=90°,∠B=40°. 请用尺规作图法,在△ABC内部求作一点P,使∠BAP=50°,且点P到AB, BC边的距离相等.(保留作图痕迹,不写作法)
18. (本题满分 8分, 每题4分)
(1)解不等式组 x-2x-1≥12x-13-5x+12<1, (2)解方程: x2x-3+4=53-2x.
19.(本题满分 6分)先化简,再求值: xx-3-13-x÷x+1x2-9,其中 x=2-3.
20. (本题满分8分) 如图,在△ABC中,∠B=∠C=30°,AD是BC边上的中线,作CD的垂直平分线MF交AC于F , 交BC于M.
(1)求证: △ADF是等边三角形;
(2)若 AB=12,求线段MF的长.
21. (本题满分8分)为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.经了解,甲水果的进价比乙水果的进价低20%,水果店用1000 元购进甲种水果比用1200元购进乙种水果的重量多10千克,已知甲,乙两种水果的售价分别为 6 元/千克和8元/千克.
(1)求甲、乙两种水果的进价分别是多少?
(2)若水果店购进这两种水果共150千克,其中甲种水果的重量不低于乙种水果重量的2倍,则水果店应如何进货才能获得最大利润,最大利润是多少?
22. (本题满分8分) 如图, 在四边形ABCD中, AD‖BC,AB=3,BC=5,连接BD, ∠BAD的平分线分别交 BD、BC于点E、F, 且. AE‖CD.
(1) 求AD 的长;
(2) 若 ∠C=30°,求 CD 的长.
23. (本题满分 10分)小明在观看2024年世界泳联世锦赛后对游泳产生了浓厚的兴趣,计划在假期练习游泳.体育中心的室内游泳馆为前来游泳的市民提供会员卡支付和按次支付两种支付方式.如图表示会员卡支付应付金额. y₁(元),按次支付应付金额 y₂(元)与游泳次数 x(次)之间的函数关系,根据图象回答下列问题:
(1)分别求 y₁、y₂关于x的函数关系式;
(2)小明用于游泳的预算为480元,若小明用会员卡支付最多可以游多少次?
(3)若小明假期想在游泳馆练习游泳,请你帮他分析选择哪种支付方式更合算?
24. (本题满分 10分) 直线y=-x+6与x轴交于A,与y轴交于B, 直线CD与y轴交于C(0,2)与直线AB交于 D, 过 D作DE⊥x轴于E(3,0).
(1)点 A 坐标为 ;点 D 坐标为 .
(2)求直线 CD 的函数关系式.
(3)P 是线段OA 上一动点,点P从原点O开始,每秒1个单位长度的速度向A运动(P与O、A不重合) ,过P作x轴的垂线,分别与直线AB、CD 交于M、N, 设四边形 MNED 的面积为S,P点运动的时间为t,求出S与t之间的函数关系式.
(4)在 (3)的条件下,当t= 时,以M、N、E、D为顶点的四边形是平行四边形.
25. (本题满分10分)综合与实践
【问题情境】
为了研究折纸过程中蕴涵的数学知识,老师发给每位同学完全相同的纸片,纸片形状如图1,在四边形ABCD中( BC≥CD,AB‖CD,∠B=90°.
【探究实践】
老师引导同学们在边BC 上任取一点 E,连接DE,将 △DCE沿DE 翻折,点C的对应点为 H,然后将纸片展平,连接CH 并延长,分别交DE,AB于点 M,G.老师让同学们探究:当点E在不同位置时,能有哪些发现?经过思考和讨论,小莹、小明向同学们分享了自巳的发现.
(1) 如图2, 小莹发现:“当折痕DE与AD夹角为90°时, 则四边形 AGCD 是平行四边形”.请你判断小莹的结论是否正确,并说明理由.
(2) 如图3, 小明发现:“当E是BC的中点时,延长DH交AB于点 N, 连接EN,则N是BG的中点”,请你判断小明的结论是否正确,并说明理由.
山东省青岛市即墨区2023-2024学年八年级下学期期中数学试题(原卷版+解析版): 这是一份山东省青岛市即墨区2023-2024学年八年级下学期期中数学试题(原卷版+解析版),文件包含山东省青岛市即墨区2023-2024学年八年级下学期期中数学试题原卷版docx、山东省青岛市即墨区2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
山东省青岛市即墨区2023-2024学年八年级下学期期中数学试题: 这是一份山东省青岛市即墨区2023-2024学年八年级下学期期中数学试题,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
山东省青岛市即墨区2023-2024学年七年级上学期期末数学试题(): 这是一份山东省青岛市即墨区2023-2024学年七年级上学期期末数学试题(),共5页。试卷主要包含了选择题,填空题,作图题,解答题等内容,欢迎下载使用。












