2023-2024学年河南省商丘市虞城县七年级（下）月考数学试卷（含答案）

这是一份2023-2024学年河南省商丘市虞城县七年级（下）月考数学试卷（含答案），共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.在实数227， 2，π，，3.1212212221…，2+ 3中，无理数的个数有( )
A. 5个B. 4个C. 3个D. 2个
2.如图，直线AB与CD相交于点O，若∠AOD=3∠AOC，则∠BOD的度数为( )
A. 30°
B. 35°
C. 40°
D. 45°
3.在平面直角坐标系中，点M(−6,4)在( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
4.下列说法正确的是( )
A. 9的算术平方根是3B. 0的算术平方根是0
C. −16的平方根是−4D. 0.1的立方根是0.001
5.用代入消元法解方程组y=2x+1,①5x−2y=7,②将①代入②可得( )
A. 5x−4x−2=7B. 5x−2x−1=7C. 5x−4x+1=7D. 5x−4x+2=7
6.一个正方形的面积为28，则它的边长应在( )
A. 3到4之间B. 4到5之间C. 5到6之间D. 6到7之间
7.如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是( )
A. 30°B. 25°C. 20°D. 15°
8.已知方程组2x−y=7a−52y−x=5的解x，y互为相反数，则a的值为( )
A. 0B. 1C. −1D. 2
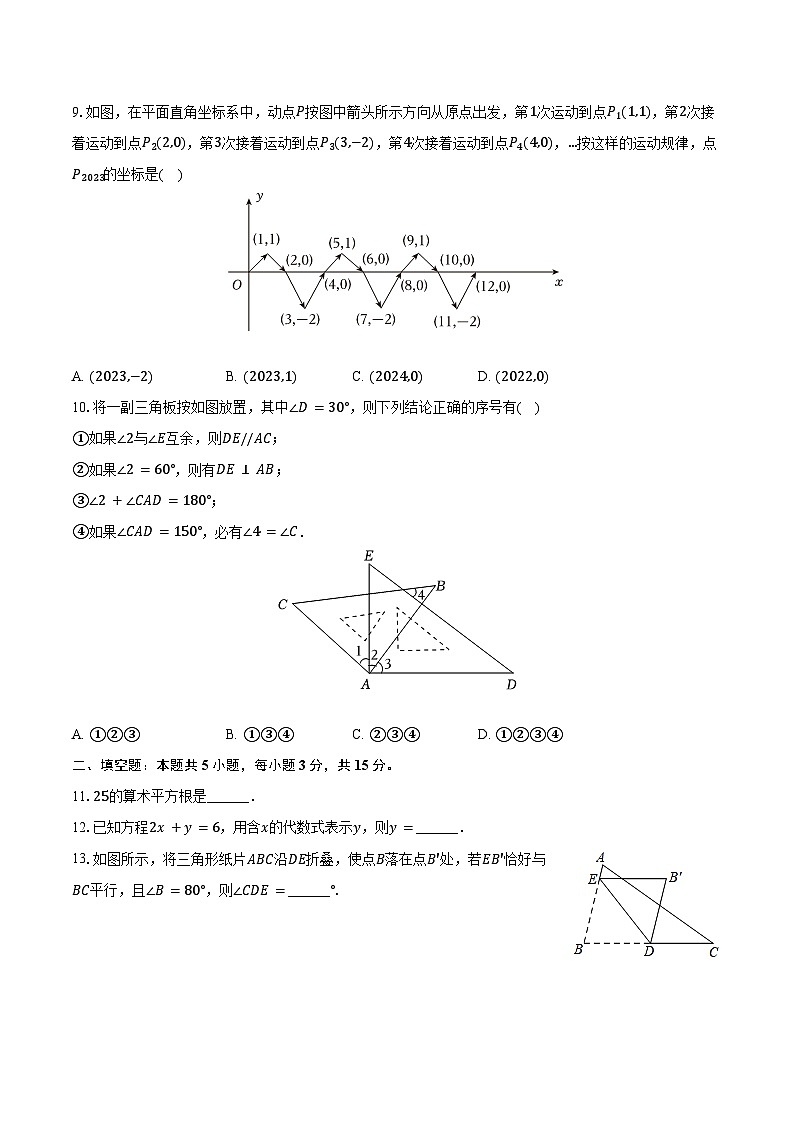
9.如图，在平面直角坐标系中，动点P按图中箭头所示方向从原点出发，第1次运动到点P1(1,1)，第2次接着运动到点P2(2,0)，第3次接着运动到点P3(3,−2)，第4次接着运动到点P4(4,0)，…按这样的运动规律，点P2023的坐标是( )
A. (2023,−2)B. (2023,1)C. (2024,0)D. (2022,0)
10.将一副三角板按如图放置，其中∠D=30°，则下列结论正确的序号有( )
①如果∠2与∠E互余，则DE/​/AC；
②如果∠2=60°，则有DE⊥AB；
③∠2+∠CAD=180°；
④如果∠CAD=150°，必有∠4=∠C．
A. ①②③B. ①③④C. ②③④D. ①②③④
二、填空题：本题共5小题，每小题3分，共15分。
11.25的算术平方根是______．
12.已知方程2x+y=6，用含x的代数式表示y，则y=______．
13.如图所示，将三角形纸片ABC沿DE折叠，使点B落在点B′处，若EB′恰好与BC平行，且∠B=80°，则∠CDE=______°.
14.如果点p(x,y)的坐标满足x+y=xy，那么称点P为“美丽点”，若某个“美丽点”M到y轴的距离为2，则点M的坐标为______．
15.在同一平面内，∠A与∠B的一组边平行，另一组边垂直，且∠A比∠B的3倍少10°，则∠B=______．
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题10分)
计算：
(1)| 3−2|+3−27− 49；
(2)解方程：27(x+1)3+64=0．
17.(本小题10分)
解下列方程组：
(1)2x−y=4x+y=8；
(2)4x−2y=22x+3y=−7．
18.(本小题8分)
小萌知道x=1y=−1和x=2y=2都是二元一次方程ax+by+4=0的解，请你帮她求出a3b的立方根．
19.(本小题9分)
阅读下面的推理过程，在括号里或横线上填写结论或理由如图，AB/​/CD/​/GH，EG平分∠BEF，FG平分∠EFD，求证：∠EGF=90°．
完成下面的证明：
证明：∵GH//AB(已知)，
∴∠1=∠3．______
又∵GH//CD(已知)，
∴∠2=∠4．______
∵AB//CD(已知)，
∴∠BEF+ ______=180°．______
∵EG平分∠BEF(已知)，FG平分∠EFD(已知)，
∴∠1=12 ______.∠2=12 ______．
∴∠1+∠2=12(______+ ______)，即∠1+∠2=90°，
∴∠3+∠4=90° ______，即∠EGF=90°
20.(本小题9分)
如图，在平面直角坐标系xOy中，A、B、C三点的坐标分别为(−5,4)、(−3,0)、(0,2)．
(1)画出三角形ABC，并求其面积；
(2)如图，△A′B′C′是由△ABC经过______平移得到的．
(3)已知点P(a,b)为△ABC内的一点，则点P在△A′B′C′内的对应点P′的坐标是(______，______).
21.(本小题9分)
如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为(a,0)，点C的坐标为(0,b)，且a、b满足 a−4+|b−6|=O，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O→A→B→C→O的线路移动
(1)求点B的坐标．
(2)当点P移动4秒时，请求出点P的坐标．
(3)当点P移动到距离x轴5个单位长度时，求点P移动的时间．
22.(本小题10分)
随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具．某汽车销售公司计划购进一批新能源汽车尝试进行销售，据了解2辆A型汽车、3辆B型汽车的进价共计80万元；3辆A型汽车、2辆B型汽车的进价共计95万元
(1)求A、B两种型号的汽车每辆进价分别为多少万元？
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买)，请你帮助该公司设计购买方案；
(3)若该汽车销售公司销售1辆A型汽车可获利8000元，销售1辆B型汽车可获利5000元，在(2)中的购买方案中，假如这些新能源汽车全部售出，哪种方案获利最大？最大利润是多少元？
23.(本小题10分)
如图1，在直角三角形ABC中，∠CAB=90°，∠C=30°，现将△ABC绕点A顺时针旋转α角度得到△ADE．

(1)若α=28°时，则∠DAC= ______°；若0°<α<90°时，α与∠CAE的关系是______；
(2)∠DAC与∠BAE有怎样的关系？请说明理由；
(3)在旋转过程中，若0°<α<180°时，△ADE与△ABC这两个三角形是否存在一组边互相平行？若存在，请求出α的所有可能取值．
参考答案
1.B
2.D
3.B
4.B
5.A
6.C
7.B
8.A
9.A
10.B
11.5
12.6−2x
13.130
14.(2,2)或(−2,23)
15.50°或25°
16.解：(1)| 3−2|+3−27− 49
=2− 3+(−3)−7
=−8− 3；
(2)27(x+1)3+64=0，
27(x+1)3=−64，
(x+1)3=−6427，
x+1=−43，
x=−73．
17.解：(1)2x−y=4①x+y=8②，
①+②，得3x=12，
解得x=4，
把x=4代入②，得y=4，
故原方程组的解为x=4y=4；
(2)4x−2y=2①2x+3y=−7②，
②×2−①，得8y=−16，
解得y=−2，
把y=−2代入①，得4x+4=2，
解得x=−12，
故原方程组的解为x=−12y=−2．
18.解：把x=1y=−1和x=2y=2代入二元一次方程ax+by+4=0得：
得：a−b+4=02a+2b+4=0，
解得：a=−3b=1，
则a3b=(−3)3×1=−27，
因此，a3b的立方根是−3．
19.两直线平行，内错角相等 两直线平行，内错角相等 ∠EFD 两直线平行，同旁内角互补 ∠BEF ∠EFD ∠BEF ∠EFD 等量代换
20.△ABC向右平移4个单位，再向下平移3个单位得到△A′B′C′， a+4 b−3
21.解：(1)∵a、b满足 a−4+|b−6|=0，
∴a−4=0，b−6=0，
解得a=4，b=6，
∴点B的坐标是(4,6)；
(2)∵点P从原点出发，以每秒2个单位长度的速度沿着O→A→B→C→O的线路移动，
∴点P的路程：2×4=8，
∵OA=4，OC=6，
∴当点P移动4秒时，在线段AB上，AP=8−6=2，
即当点P移动4秒时，此时点P的坐标是(6,2)；
(3)由题意可得，在移动过程中，当点P到x轴的距离为5个单位长度时，存在两种情况，
第一种情况，当点P在OC上时，
点P移动的时间是：[2(4+6)−5]÷2=7.5(秒)，
第二种情况，当点P在BA上时．
点P移动的时间是：(5+4)÷2=4.5(秒)，
故在移动过程中，当点P到x轴的距离为5个单位长度时，点P移动的时间是7.5秒或4.5秒．
22.解：(1)设A型汽车每辆的进价为x万元，B型汽车每辆的进价为y万元，
依题意，得：2x+3y=803x+2y=95，
解得：x=25y=10．
答：A型汽车每辆的进价为25万元，B型汽车每辆的进价为10万元．
(2)设购进A型汽车m辆，购进B型汽车n辆，
依题意，得：25m+10n=200，
解得：m=8−25n.
∵m，n均为正整数，
∴m1=6n1=5，m2=4n2=10，m3=2n3=15，
∴共3种购买方案，方案一：购进A型车6辆，B型车5辆；方案二：购进A型车4辆，B型车10辆；方案三：购进A型车2辆，B型车15辆．
(3)方案一获得利润：8000×6+5000×5=73000(元)；
方案二获得利润：8000×4+5000×10=82000(元)；
方案三获得利润：8000×2+5000×15=91000(元)．
∵73000<82000<91000，
∴购进A型车2辆，B型车15辆获利最大，最大利润是91000元．
23.62 α=∠CAE