江苏省淮安市淮阴区2023-2024学年八年级下学期期末数学试题

这是一份江苏省淮安市淮阴区2023-2024学年八年级下学期期末数学试题，共18页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。

1．（3分）剪纸是中国优秀的传统文化．下列剪纸图案中，是轴对称图形的是（ ）
A．B．
C．D．
2．（3分）下列性质中，矩形具有而菱形不一定具有的是（ ）
A．对角线相等B．对角线互相平分
C．对角线互相垂直D．邻边相等
3．（3分）一元二次方程x2﹣9＝0的根为（ ）
A．3B．﹣3C．3或﹣3D．0
4．（3分）若分式的值为0，则x应满足的条件是（ ）
A．x＝2B．x＝﹣2C．x≠2D．x≠﹣2
5．（3分）关于x的方程2x2+mx+n＝0的两个根是﹣2和1，则nm的值为（ ）
A．﹣8B．8C．16D．﹣16
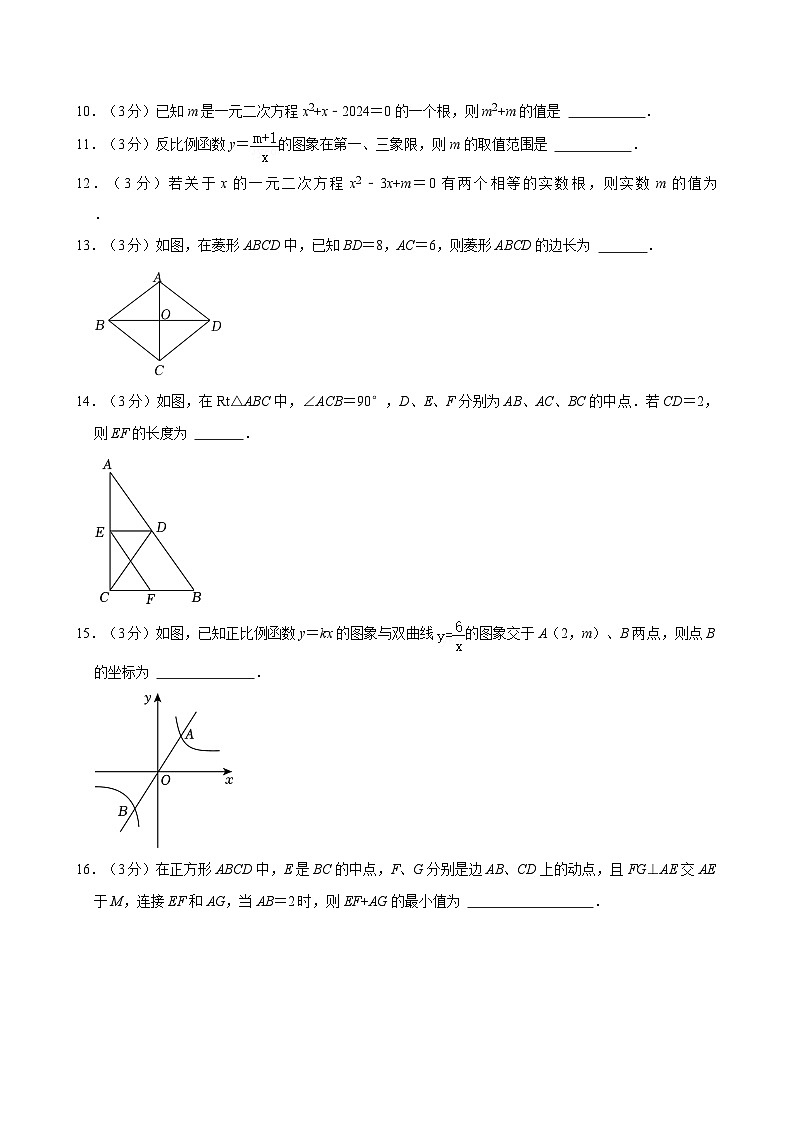
6．（3分）关于x的分式方程有增根，则m的值为（ ）
A．2B．1C．﹣3D．3
7．（3分）用配方法解一元二次方程x2﹣6x+8＝0，配方后得到的方程是（ ）
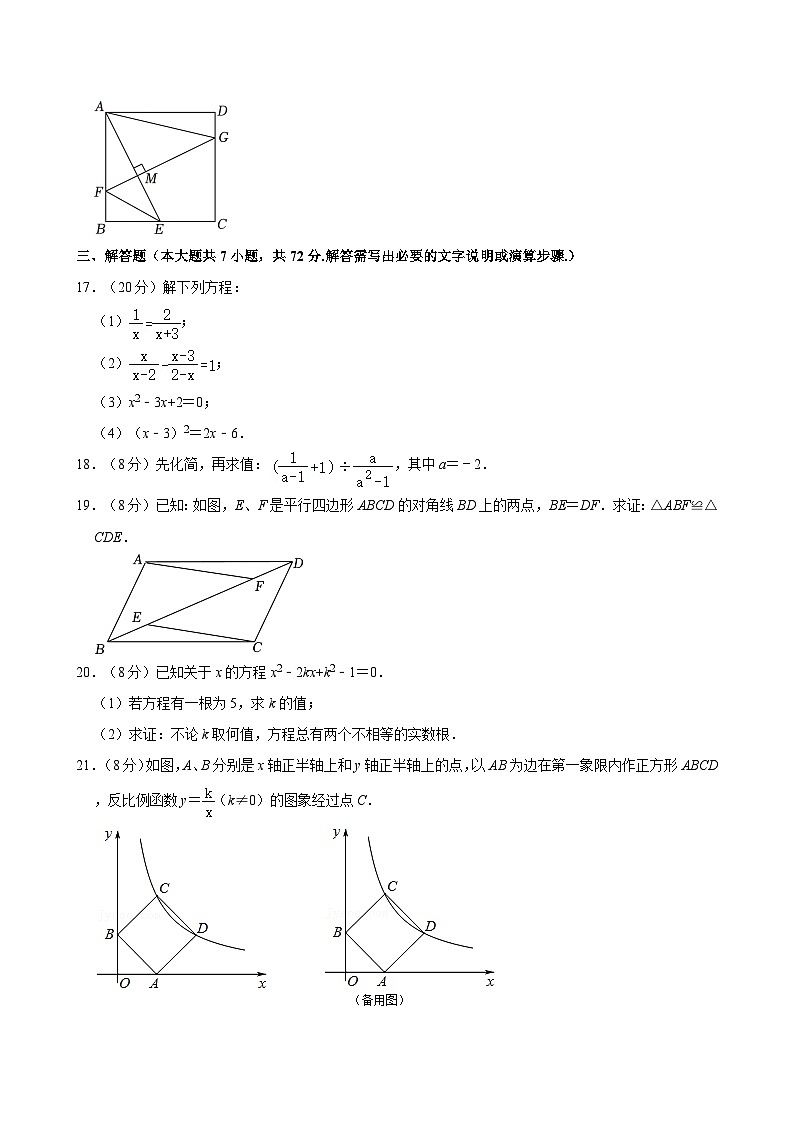
A．（x+6）2＝17B．（x﹣6）2＝17C．（x+3）2＝1D．（x﹣3）2＝1
8．（3分）函数与y＝﹣2x+3的图象交于点P（a，b），则代数式的值是（ ）
A．B．C．﹣2D．2
二.填空题（本大题有8小题，每小题3分，共24分）
9．（3分）若分式有意义，则x的取值范围是 ．
10．（3分）已知m是一元二次方程x2+x﹣2024＝0的一个根，则m2+m的值是 ．
11．（3分）反比例函数y＝的图象在第一、三象限，则m的取值范围是 ．
12．（3分）若关于x的一元二次方程x2﹣3x+m＝0有两个相等的实数根，则实数m的值为 ．
13．（3分）如图，在菱形ABCD中，已知BD＝8，AC＝6，则菱形ABCD的边长为 ．
14．（3分）如图，在Rt△ABC中，∠ACB＝90°，D、E、F分别为AB、AC、BC的中点．若CD＝2，则EF的长度为 ．
15．（3分）如图，已知正比例函数y＝kx的图象与双曲线的图象交于A（2，m）、B两点，则点B的坐标为 ．
16．（3分）在正方形ABCD中，E是BC的中点，F、G分别是边AB、CD上的动点，且FG⊥AE交AE于M，连接EF和AG，当AB＝2时，则EF+AG的最小值为 ．
三、解答题（本大题共7小题，共72分.解答需写出必要的文字说明或演算步骤.）
17．（20分）解下列方程：
（1）；
（2）；
（3）x2﹣3x+2＝0；
（4）（x﹣3）2＝2x﹣6．
18．（8分）先化简，再求值：，其中a＝﹣2．
19．（8分）已知：如图，E、F是平行四边形ABCD的对角线BD上的两点，BE＝DF．求证：△ABF≌△CDE．
20．（8分）已知关于x的方程x2﹣2kx+k2﹣1＝0．
（1）若方程有一根为5，求k的值；
（2）求证：不论k取何值，方程总有两个不相等的实数根．
21．（8分）如图，A、B分别是x轴正半轴上和y轴正半轴上的点，以AB为边在第一象限内作正方形ABCD，反比例函数y＝（k≠0）的图象经过点C．
（1）若点C坐标为（2，3），则k的值为 ；
（2）若A、B两点坐标分别A（2，0），B（0，2）；
①则k的值为 ；
②此时点D （填“在”、“不在”或者“不一定在”）该反比例函数的图象上；
（3）若C、D两点都在函数y＝的图象上，直接写出点C的坐标为 ．
22．（8分）如图均是6×6的正方形网格，每个小正方形的顶点称为格点．△ABC的顶点均在格点上，M是AB与网格线的交点，只用无刻度的直尺，分别在给定的网格中按下列要求作图，保留作图痕迹．
（1）在图①中，在格点上找一点D，并连结DB、CD，使△DBC和△ABC全等；
（2）在图②中，作点M关于BC的对称点N；
（3）在图③中，在BC边上找一点E，连结ME，使ME＝MB．
23．（12分）综合与实践
如图1，某兴趣小组计划开垦一个面积为8m2的矩形地块ABCD种植农作物，地块一边靠墙，另外三边用木栏围住，木栏总长为a m．
【问题提出】
小组同学提出这样一个问题：若a＝10，能否围出矩形地块？
【问题探究】
小颖尝试从“函数图象”的角度解决这个问题：
设AB为x m，BC为y m．由矩形地块面积为8m2，得到xy＝8，满足条件的（x，y）可看成是反比例函数y＝的图象在第一象限内点的坐标；木栏总长为10m，得到2x+y＝10，满足条件的（x，y）可看成一次函数y＝﹣2x+10的图象在第一象限内点的坐标，同时满足这两个条件的（x，y）就可以看成两个函数图象交点的坐标．
如图2，反比例函数y＝（x＞0）的图象与直线l1：y＝﹣2x+10的交点坐标为（1，8）和 ，因此，木栏总长为10m时，能围出矩形地块，分别为：AB＝1m，BC＝8m；或AB＝ m，BC＝ m．
（1）根据小颖的分析思路，完成上面的填空；
【类比探究】
（2）若a＝6，能否围出矩形地块？请仿照小颖的方法，在图2中画出一次函数图象并说明理由；
【问题延伸】
当木栏总长为a m时，小颖建立了一次函数y＝﹣2x+a．发现直线y＝﹣2x+a可以看成是直线y＝﹣2x通过平移得到的，在平移过程中，当过点（2，4）时，直线y＝﹣2x+a与反比例函数y＝（x＞0）的图象有唯一交点．
（3）请在图2中画出直线y＝﹣2x+a过点（2，4）时的图象，并求出a的值；
【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“y＝﹣2x+a与y＝图象在第一象限内交点的存在问题”．
若要围出满足条件的矩形地块，且AB和BC的长均不小于1m，请直接写出a的取值范围．
参考答案与试题解析
一、选择题（每小题3分，共24分）
1．（3分）剪纸是中国优秀的传统文化．下列剪纸图案中，是轴对称图形的是（ ）
A．B．
C．D．
【解答】解：A、选项不是轴对称图形，不符合题意；
B、选项关于某条直线对称，是轴对称图形，符合题意；
C、选项不是轴对称图形，不符合题意；
D、选项不是轴对称图形，不符合题意；
故选：B．
2．（3分）下列性质中，矩形具有而菱形不一定具有的是（ ）
A．对角线相等B．对角线互相平分
C．对角线互相垂直D．邻边相等
【解答】解：矩形的性质有：①矩形的对边平行且相等，②矩形的四个角都是直角，③矩形的对角线互相平分且相等；
菱形的性质有：①菱形的对边平行，菱形的四条边都相等，②菱形的对角相等，③菱形的对角线互相平分且垂直，并且每一条对角线平分一组对角，所以矩形具有而菱形不一定具有的性质是对角线相等，
故选：A．
3．（3分）一元二次方程x2﹣9＝0的根为（ ）
A．3B．﹣3C．3或﹣3D．0
【解答】解：移项得x2＝9，∴x＝±3．故选C．
4．（3分）若分式的值为0，则x应满足的条件是（ ）
A．x＝2B．x＝﹣2C．x≠2D．x≠﹣2
【解答】解：∵分式的值为0，
∴x﹣2＝0，即x+2≠0，
∴x＝2．
故选：A．
5．（3分）关于x的方程2x2+mx+n＝0的两个根是﹣2和1，则nm的值为（ ）
A．﹣8B．8C．16D．﹣16
【解答】解：∵关于x的方程2x2+mx+n＝0的两个根是﹣2和1，
∴﹣＝﹣1，＝﹣2，
∴m＝2，n＝﹣4，
∴nm＝（﹣4）2＝16．
故选：C．
6．（3分）关于x的分式方程有增根，则m的值为（ ）
A．2B．1C．﹣3D．3
【解答】解：方程两边都乘（x﹣2），得m+3＝x﹣2，
∵原方程增根为x＝2，
∴把x＝2代入整式方程，得m＝﹣3．
故选：C．
7．（3分）用配方法解一元二次方程x2﹣6x+8＝0，配方后得到的方程是（ ）
A．（x+6）2＝17B．（x﹣6）2＝17C．（x+3）2＝1D．（x﹣3）2＝1
【解答】解：x2﹣6x+8＝0，
x2﹣6x＝﹣8，
x2﹣6x+9＝﹣8+9，
（x﹣3）2＝1，
故选：D．
8．（3分）函数与y＝﹣2x+3的图象交于点P（a，b），则代数式的值是（ ）
A．B．C．﹣2D．2
【解答】解：把点P（a，b）代入函数与y＝﹣2x+3中得：
，﹣2a+3＝b，
整理得ab＝﹣6，2a+b＝3，
∴
＝
＝
＝
＝﹣．
故选：A．
二.填空题（本大题有8小题，每小题3分，共24分）
9．（3分）若分式有意义，则x的取值范围是 x≠5 ．
【解答】解：∵分式有意义，
∴x﹣5≠0，解得：x≠5．
故答案为：x≠5．
10．（3分）已知m是一元二次方程x2+x﹣2024＝0的一个根，则m2+m的值是 2024 ．
【解答】解：∵m是一元二次方程x2+x﹣2024＝0的一个根，
∴m2+m﹣2024＝0，
∴m2+m＝2024．
故答案为：2024．
11．（3分）反比例函数y＝的图象在第一、三象限，则m的取值范围是 m＞﹣1 ．
【解答】解：根据题意得m+1＞0，
解得m＞﹣1．
故答案为：m＞﹣1．
12．（3分）若关于x的一元二次方程x2﹣3x+m＝0有两个相等的实数根，则实数m的值为 ．
【解答】解：∵关于x的一元二次方程x2﹣3x+m＝0有两个相等的实数根，
∴Δ＝（﹣3）2﹣4m＝0，
解得m＝．
故答案为：．
13．（3分）如图，在菱形ABCD中，已知BD＝8，AC＝6，则菱形ABCD的边长为 5 ．
【解答】解：∵四边形ABCD是菱形，
∴AC⊥BD，AO＝AC＝3，BO＝BD＝4，
∴AB＝＝＝5，
故答案为：5．
14．（3分）如图，在Rt△ABC中，∠ACB＝90°，D、E、F分别为AB、AC、BC的中点．若CD＝2，则EF的长度为 2 ．
【解答】解：在Rt△ABC中，∠ACB＝90°，D为AB的中点，CD＝2，
则AB＝2CD＝4，
∵E、F分别为AC、BC的中点，
∴EF是△ABC的中位线，
∴EF＝AB＝2，
故答案为：2．
15．（3分）如图，已知正比例函数y＝kx的图象与双曲线的图象交于A（2，m）、B两点，则点B的坐标为 （﹣2，﹣3） ．
【解答】解：∵双曲线的图象过点A（2，m），
∴m＝＝3，
∴A（2，3），
∵反比例函数的图象与正比例函数的图象均关于原点对称，
∴A、B两点关于原点对称，
∴B（﹣2，﹣3）．
16．（3分）在正方形ABCD中，E是BC的中点，F、G分别是边AB、CD上的动点，且FG⊥AE交AE于M，连接EF和AG，当AB＝2时，则EF+AG的最小值为 ．
【解答】解：以FE、FG为邻边作平行四边形FGNE，连接AN，过点G作GH⊥AB于点H，
∵四边形ABCD是正方形，
∴∠ABE＝∠BAD＝∠ADG＝90°，AB＝AD＝BC＝2，
∵E是BC的中点，
∴BE＝CE＝1，
在Rt△ABE中，AB＝2，BE＝1，
由勾股定理得，
∵GH⊥AB，
∴∠GHA＝∠GHF＝90°，
∴∠GHA＝∠BAD＝∠ADG＝90°，
∴四边形AHGD是矩形，
∴GH＝AD，
∴GH＝AB，
∵FG⊥AE，
∴∠AMF＝90°，
∴∠GFH+∠BAE＝90°，
∵∠AEB+∠BAE＝90°，
∴∠GFH＝∠AEB，
在△ABE和△GHF中，
，
∴△ABE≌△GHF（AAS），
∴GF＝AE＝，
∵四边形FGNE是平行四边形，
∴GF∥EN，GF＝EN＝AE＝，EF＝GN，
∴∠AEN＝∠AMG＝90°，
∴△AEN是等腰直角三角形，
∴，
∵AG+GN≥AN，
∴当A、G、N在一条直线上时AG+GN最小，即AG+EF最小，此时最小值是AN的长，为，
故答案为：．
三、解答题（本大题共7小题，共72分.解答需写出必要的文字说明或演算步骤.）
17．（20分）解下列方程：
（1）；
（2）；
（3）x2﹣3x+2＝0；
（4）（x﹣3）2＝2x﹣6．
【解答】解：（1）两边同乘以最简公分母x（x+3）得，
x+3＝2x，
解得，x＝3，
检验：当x＝3时，x（x+3）＝18≠0，
∴x＝3是原方程的解；
（2）两边同乘以最简公分母（x﹣2）得，
x+x﹣3＝x﹣2，
解得，x＝1，
检验：当x＝1时，x﹣2≠0，
∴x＝1是原方程的解；
（3）x2﹣3x+2＝0，
（x﹣2）（x﹣1）＝0，
∴x﹣2＝0或x﹣1＝0，
∴x1＝2，x2＝1；
（4））（x﹣3）2＝2x﹣6，
（x﹣3）2﹣2（x﹣3）＝0，
（x﹣3）（x﹣3﹣2）＝0，
∴x﹣3＝0或x﹣5＝0，
∴x1＝3，x2＝5．
18．（8分）先化简，再求值：，其中a＝﹣2．
【解答】解：原式＝（+）•
＝•
＝a+1，
当a＝﹣2时，原式＝﹣2+1＝﹣1．
19．（8分）已知：如图，E、F是平行四边形ABCD的对角线BD上的两点，BE＝DF．求证：△ABF≌△CDE．
【解答】证明：∵四边形ABCD是平行四边形，
∴AB＝CD，AB∥CD，
∴∠ABF＝∠CDE，
∵BE＝DF，
∴BD﹣BE＝BD﹣DF，
即DE＝BF，
在△ABF和△CDE中，
，
∴△ABF≌△CDE（SAS）．
20．（8分）已知关于x的方程x2﹣2kx+k2﹣1＝0．
（1）若方程有一根为5，求k的值；
（2）求证：不论k取何值，方程总有两个不相等的实数根．
【解答】（1）解：x＝＝k±1，
解得x1＝k+1，x2＝k﹣1，
当k+1＝5时，k＝4；
当k﹣1＝5时，k＝6，
综上所述，k的值为4或6；
（2）证明：∵Δ＝（﹣2k）2﹣4（k2﹣1）
＝4＞0，
∴不论k取何值，方程总有两个不相等的实数根．
21．（8分）如图，A、B分别是x轴正半轴上和y轴正半轴上的点，以AB为边在第一象限内作正方形ABCD，反比例函数y＝（k≠0）的图象经过点C．
（1）若点C坐标为（2，3），则k的值为 6 ；
（2）若A、B两点坐标分别A（2，0），B（0，2）；
①则k的值为 8 ；
②此时点D 在 （填“在”、“不在”或者“不一定在”）该反比例函数的图象上；
（3）若C、D两点都在函数y＝的图象上，直接写出点C的坐标为 （1，2） ．
【解答】解：（1）由题意得，当x＝2，y＝，则k＝6．
故答案为：6．
（2）∵A（2，0），B（0，2），四边形ABCD是正方形，
∴C（2，4），D（4，2）．
∴当x＝2，y＝．
∴k＝8．
∴y＝．
∴当x＝4，则y＝．
∴D在反比例函数的图象上．
故答案为：8，在．
（3）设A（a，0），则C（a，2a），D（2a，a）．
∴2a＝，a＝．
∴a＝1或a＝﹣1（不合题意，舍去）．
∴C（1，2）．
故答案为：（1，2）．
22．（8分）如图均是6×6的正方形网格，每个小正方形的顶点称为格点．△ABC的顶点均在格点上，M是AB与网格线的交点，只用无刻度的直尺，分别在给定的网格中按下列要求作图，保留作图痕迹．
（1）在图①中，在格点上找一点D，并连结DB、CD，使△DBC和△ABC全等；
（2）在图②中，作点M关于BC的对称点N；
（3）在图③中，在BC边上找一点E，连结ME，使ME＝MB．
【解答】解：（1）如图①，点D'，D''均满足题意．
（2）如图②，取点A关于BC的对称点D，连结BD交网格线于点N，
则点N即为所求．
（3）如图③，取格点P，Q，使AP∥BQ，且AP＝BQ＝AB，分别取BQ和AP与网格线的交点M，N，连结MN，交BC于点E，连结ME，
则点E即为所求．
23．（12分）综合与实践
如图1，某兴趣小组计划开垦一个面积为8m2的矩形地块ABCD种植农作物，地块一边靠墙，另外三边用木栏围住，木栏总长为a m．
【问题提出】
小组同学提出这样一个问题：若a＝10，能否围出矩形地块？
【问题探究】
小颖尝试从“函数图象”的角度解决这个问题：
设AB为x m，BC为y m．由矩形地块面积为8m2，得到xy＝8，满足条件的（x，y）可看成是反比例函数y＝的图象在第一象限内点的坐标；木栏总长为10m，得到2x+y＝10，满足条件的（x，y）可看成一次函数y＝﹣2x+10的图象在第一象限内点的坐标，同时满足这两个条件的（x，y）就可以看成两个函数图象交点的坐标．
如图2，反比例函数y＝（x＞0）的图象与直线l1：y＝﹣2x+10的交点坐标为（1，8）和 （4，2） ，因此，木栏总长为10m时，能围出矩形地块，分别为：AB＝1m，BC＝8m；或AB＝ 4 m，BC＝ 2 m．
（1）根据小颖的分析思路，完成上面的填空；
【类比探究】
（2）若a＝6，能否围出矩形地块？请仿照小颖的方法，在图2中画出一次函数图象并说明理由；
【问题延伸】
当木栏总长为a m时，小颖建立了一次函数y＝﹣2x+a．发现直线y＝﹣2x+a可以看成是直线y＝﹣2x通过平移得到的，在平移过程中，当过点（2，4）时，直线y＝﹣2x+a与反比例函数y＝（x＞0）的图象有唯一交点．
（3）请在图2中画出直线y＝﹣2x+a过点（2，4）时的图象，并求出a的值；
【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“y＝﹣2x+a与y＝图象在第一象限内交点的存在问题”．
（4）若要围出满足条件的矩形地块，且AB和BC的长均不小于1m，请直接写出a的取值范围．
【解答】解：（1）将反比例函数y＝与直线l1：y＝﹣2x+10联立得
，
∴＝﹣2x+10，
∴x2﹣5x+4＝0，
∴x1＝1，x2＝4，
∴另一个交点坐标为（4，2），
∵AB为x m，BC为y m，
∴AB＝4，BC＝2．
故答案为：（4，2）；4；2；
（2）不能围出；
y＝﹣2x+6的图象，如答案图中l2所示：
∵l2 与函数 图象没有交点，
∴不能围出面积为 8m2的矩形．
（3）如答案图中直线l3所示：
将点（2，4）代入y＝﹣2x+a，解得a＝8．
（4）∵AB和BC的长均不小于1m，
∴x≥1，y≥1，
∴≥1，
∴x≤8，
∴1≤x≤8，
如图所示，直线y＝﹣2x+a在l3、l4上面或之间移动，
把（8，1）代入y＝﹣2x+a得a＝17，
∴8≤a≤17．