浙教版九年级上册3.3 垂径定理备课ppt课件

这是一份浙教版九年级上册3.3 垂径定理备课ppt课件，共26页。PPT课件主要包含了知识点，垂径定理的逆定理，探索一，如果弦CD是直径呢，垂径定理的推论1，探索二，垂径定理的推论2等内容，欢迎下载使用。

经历探索垂径定理的推论的过程，掌握垂径定理的推论．学会运用垂径定理的推论解决有关弦、弧、弦心距以及半径之间的证明和计算问题．
我国历史上著名的赵州桥建于隋大业(公元605~618)年间，桥长64.40m，是现存世界上跨径最大、建造最早的单孔敞肩型石拱桥.你知道怎样确定桥拱圆弧的半径吗？
垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧.
反过来，平分弦的直径一定垂直于这条弦吗？平分弧的直径一定垂直于弧所对的弦吗？
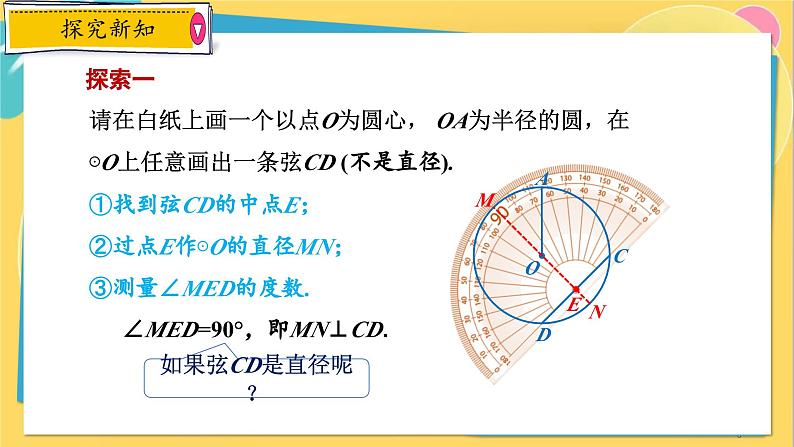
请在白纸上画一个以点O为圆心， OA为半径的圆，在⊙O上任意画出一条弦CD (不是直径).
①找到弦CD的中点E；②过点E作⊙O的直径MN；③测量∠MED的度数.
∠MED=90°，即MN⊥CD.
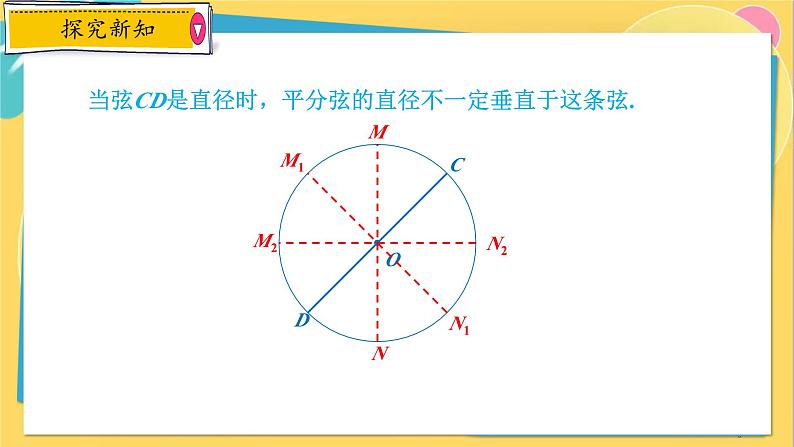
当弦CD是直径时，平分弦的直径不一定垂直于这条弦.
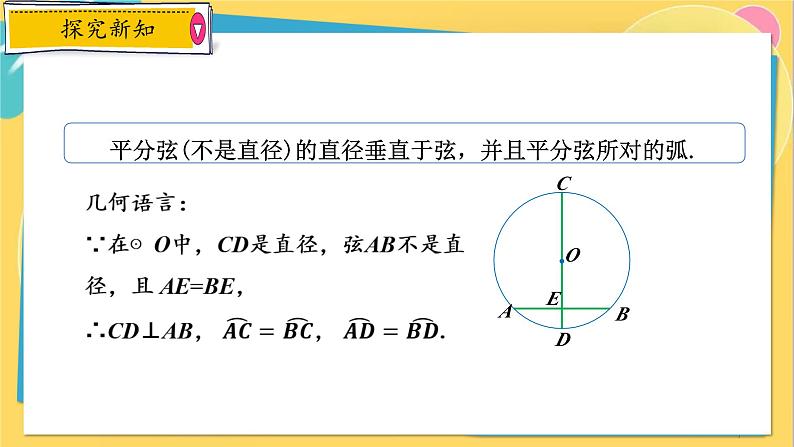
平分弦(不是直径)的直径垂直于弦，并且平分弦所对的弧.
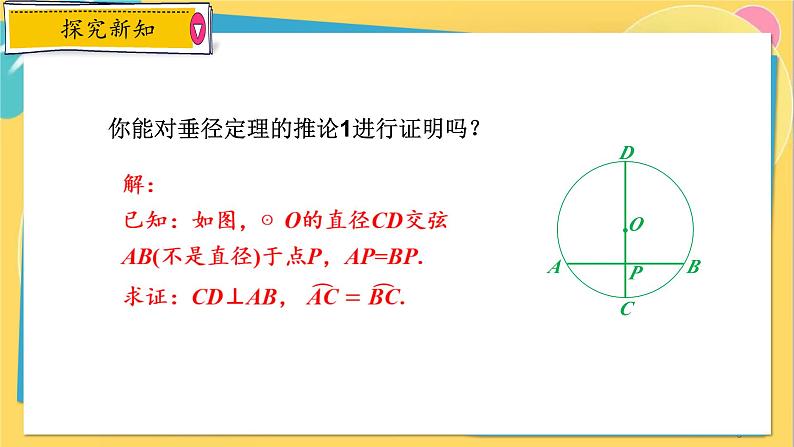
你能对垂径定理的推论1进行证明吗？
请在白纸上画一个以点O为圆心， OA为半径的圆，在⊙O上任意找出一段弧CD，连结CD.
①找到弧CD的中点E；②过点E作⊙O的直径EF，交弦CD于点P；③测量∠FPD的度数.
∠FPD=90°，即EF⊥CD.
平分弧的直径垂直平分弧所对的弦.
你能对垂径定理的推论2进行证明吗？
所以点A与点B重合，即A，B关于直线CD对称，所以CD垂直平分弦AB，这就证明了推论2.
比较垂径定理、推论1、推论2的条件和结论，你发现了什么？
垂径定理及其推论可以看成由五个事项构成：①两条弦互相垂直； ②一条弦经过圆心；③一条弦(不是直径)被平分； ④平分弦所对的一条弧；⑤平分弦所对的另一条弧.这五个事项中，已知其中任意两个，必然能推出其余的三个.
已知赵州桥的跨径(桥拱圆弧所对的弦的长)为37.02m，拱高(桥拱圆弧的中点到弦的距离)为7.23m，求赵州桥的桥拱圆弧的半径(精确到0.1m)．
垂径定理推论的实际应用
如图，武汉晴川桥可以近似地看成半径为250 m的圆弧，桥拱和路面之间用数根钢索垂直相连，桥拱正下方的路面AB长度为300 m，那么这些钢索中最长的一根为(　　)A．50 m B．45 m C．40 m D．60 m
解决有关弦的问题，经常是过圆心作弦的垂线，或作垂直于弦的直径，连结半径等辅助线，为应用垂径定理创造条件.
某一条公路隧道的形状如图所示，半圆拱的圆心距离地面2m，半径为1.5m.一辆高3m，宽2.3m的集装箱卡车能顺利通过这个隧道吗？如果要使高度不超过4m，宽为2.3m的大货车也能顺利通过这个隧道，且不改变圆心到地面的距离，半圆拱的半径至少为多少米？
下列命题中，正确的是(　　)A．过弦的中点的直线平分弦所对的弧B．过弦中点的直线必经过圆心C．弦所对的两条弧的中点的连线垂直平分弦D．弦的垂线平分弦所对的弧
【2023·金华一模】如图是以点O为圆心的圆的一部分，M是⊙O中弦CD的中点，连结MO，并延长交⊙O于点E，若CD＝6，ME＝9，则⊙O的半径为(　　)A．8 B．7 C．6 D．5
如图，武汉晴川桥可以近似地看成半径为250 m的圆弧，桥拱和路面之间用数根钢索垂直相连，桥拱正下方的路面AB长度为300 m，那么这些钢索中最长的一根为(　　)A．50 m B．45 m C．40 m D．60 m