高考数学一轮复习小题多维练(新高考专用)第10练任意角、弧度制和三角函数的概念(原卷版+解析)

这是一份高考数学一轮复习小题多维练(新高考专用)第10练任意角、弧度制和三角函数的概念(原卷版+解析)，共16页。

1．(2023·辽宁丹东·一模）碾子是我国古代用人力或畜力把高粱､谷子､稻子等谷物脱壳或把米碾碎成碴子或面粉的石制农业生产工具，由碾盘､碾滚､碾柱和碾架等组成.通过碾架把碾滚的轴固定在经过碾盘圆圆心且垂直于碾盘面的碾柱上，推动碾架，让碾滚绕碾柱在碾盘面上转动3周，碾滚恰好自转了8圈，把碾滚看成高为h，底面圆的直径为d的圆柱，则h与d之比约为（ ）
A．B．C．D．
2．(2023·广东·一模）为解决皮尺长度不够的问题，实验小组利用自行车来测量A，B两点之间的直线距离.如下图，先将自行车前轮置于点A，前轮上与点A接触的地方标记为点C，然后推着自行车沿AB直线前进（车身始终保持与地面垂直），直到前轮与点B接触.经观测，在前进过程中，前轮上的标记点C与地面接触了10次，当前轮与点B接触时，标记点C在前轮的左上方（以下图为观察视角），且到地面的垂直高度为0.45m.已知前轮的半径为0.3m，则A，B两点之间的距离约为（ ）（参考数值：）
A．20.10mB．19.94mC．19.63mD．19.47m
3．(2023·江苏苏州·模拟）已知扇形的圆心角为120°，半径为3，则这个扇形的面积为（ ）
A．3B．2C．D．
4．(2023·湖北·模拟）若角的终边经过点，则的值为（ ）
A．B．C．D．
5．(2023·北京市八一中学一模）在平面直角坐标系xOy中，角θ以Ox为始边，终边经过点，则（ ）
A．B．C．D．
6．(2023·上海青浦·二模）已知角的终边过点，则的值为_________．
7．(2023·广东广州·一模）若，，则___________.
1．(2023·北京·人大附中三模）半径为的圆的边沿有一点，半径为的圆的边沿有一点，、两点重合后，小圆沿着大圆的边沿滚动，、两点再次重合小圆滚动的圈数为（ ）
A．B．C．D．
2．(2023·湖北·房县第一中学模拟）已知圆台形的花盆的上、下底面的直径分别为8和6，该花盆的侧面展开图的扇环所对的圆心角为，则母线长为（ ）
A．4B．8C．10D．16
3．(2023·广东·模拟）已知圆锥的全面积是底面积的3倍，那么这个圆锥的侧面积展开图-扇形的圆心角为（ ）
A．B．C．D．
4．(2023·浙江·高考真题）设，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件
5．(2023·江苏·常州高级中学模拟）已知角的终边在直线上，则的值为（ ）
A．B．C．0D．
6．(2023·辽宁实验中学模拟）已知，则_________．
7．(2023·山东·烟台二中模拟）已知，则______．
8．(2023·山东威海·三模）已知，，则___________.
9．(2023·湖北·荆州中学三模）若点关于轴对称点为，写出的一个取值为___．
10．(2023·广东深圳·二模）已知，则__________．
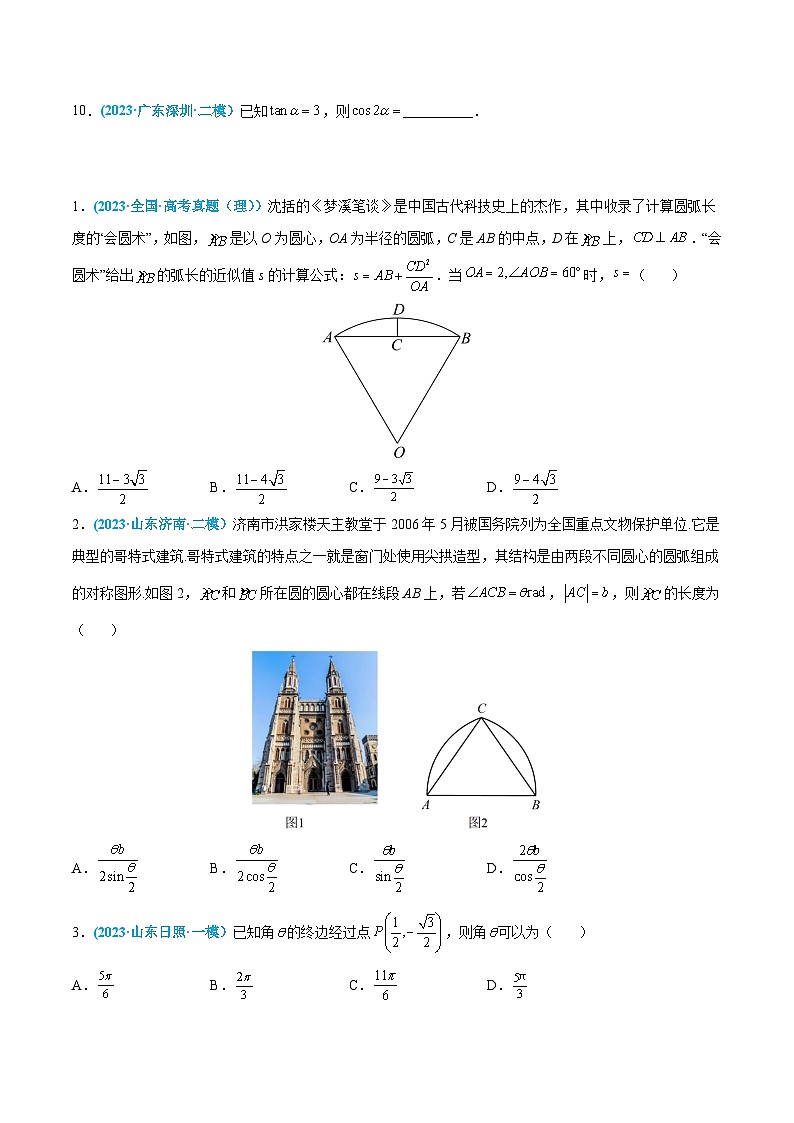
1．(2023·全国·高考真题（理））沈括的《梦溪笔谈》是中国古代科技史上的杰作，其中收录了计算圆弧长度的“会圆术”，如图，是以O为圆心，OA为半径的圆弧，C是AB的中点，D在上，．“会圆术”给出的弧长的近似值s的计算公式：．当时，（ ）
A．B．C．D．
2．(2023·山东济南·二模）济南市洪家楼天主教堂于2006年5月被国务院列为全国重点文物保护单位.它是典型的哥特式建筑.哥特式建筑的特点之一就是窗门处使用尖拱造型，其结构是由两段不同圆心的圆弧组成的对称图形.如图2，和所在圆的圆心都在线段AB上，若，，则的长度为（ ）
A．B．C．D．
3．(2023·山东日照·一模）已知角的终边经过点，则角可以为（ ）
A．B．C．D．
4．(2023·北京市第五中学三模）若点A（csθ，sinθ）与关于x轴对称，则θ的一个取值为___________.
5．(2023·浙江绍兴·模拟）勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线，它由德国机械工程专家，机构运动学家勒洛首先发现，其作法是：以等边三角形每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，三段弧围成的曲边三角形就是勒洛三角形．已知等边三角形的边长为1，则勒洛三角形的面积是_______．
6．(2023·广东广东·一模）数学中处处存在着美，机械学家莱洛发现的莱洛三角形就给人以对称的美感．莱洛三角形的画法：先画等边三角形ABC，再分别以点A、B、C为圆心，线段AB长为半径画圆弧，便得到莱洛三角（如图所示）．若莱洛三角形的周长为，则其面积是______．
7．(2023·上海市实验学校模拟）在中， 所对边分别为，若，则____________.
8．(2023·北京·101中学模拟）如图，单位圆Q的圆心初始位置在点（0，1），圆上一点P的初始位置在原点，圆沿x轴正方向滚动．当点P第一次滚动到最高点时，点P的坐标为______；当圆心Q位于点（3，1）时，点P的坐标为______．
专题04 三角函数
第10练 任意角、弧度制和三角函数的概念
1．(2023·辽宁丹东·一模）碾子是我国古代用人力或畜力把高粱､谷子､稻子等谷物脱壳或把米碾碎成碴子或面粉的石制农业生产工具，由碾盘､碾滚､碾柱和碾架等组成.通过碾架把碾滚的轴固定在经过碾盘圆圆心且垂直于碾盘面的碾柱上，推动碾架，让碾滚绕碾柱在碾盘面上转动3周，碾滚恰好自转了8圈，把碾滚看成高为h，底面圆的直径为d的圆柱，则h与d之比约为（ ）
A．B．C．D．
答案：A
【解析】设圆柱形碾滚的高为，碾盘圆的直径为，则有，所以，
于是
故选：A
2．(2023·广东·一模）为解决皮尺长度不够的问题，实验小组利用自行车来测量A，B两点之间的直线距离.如下图，先将自行车前轮置于点A，前轮上与点A接触的地方标记为点C，然后推着自行车沿AB直线前进（车身始终保持与地面垂直），直到前轮与点B接触.经观测，在前进过程中，前轮上的标记点C与地面接触了10次，当前轮与点B接触时，标记点C在前轮的左上方（以下图为观察视角），且到地面的垂直高度为0.45m.已知前轮的半径为0.3m，则A，B两点之间的距离约为（ ）（参考数值：）
A．20.10mB．19.94mC．19.63mD．19.47m
答案：D
【解析】解：由题意，前轮转动了圈，
所以A，B两点之间的距离约为，
故选：D.
3．(2023·江苏苏州·模拟）已知扇形的圆心角为120°，半径为3，则这个扇形的面积为（ ）
A．3B．2C．D．
答案：A
【解析】由扇形面积公式可得
这个扇形的面积为
故选：A
4．(2023·湖北·模拟）若角的终边经过点，则的值为（ ）
A．B．C．D．
答案：D
【解析】∵角的终边经过点，
∴，，，
∴．
故选：D．
5．(2023·北京市八一中学一模）在平面直角坐标系xOy中，角θ以Ox为始边，终边经过点，则（ ）
A．B．C．D．
答案：C
【解析】设点，因为，所以.
故选：C.
6．(2023·上海青浦·二模）已知角的终边过点，则的值为_________．
答案：
【解析】解：因为角的终边过点，
所以.
故答案为：-2.
7．(2023·广东广州·一模）若，，则___________.
答案：
【解析】解：因为，，所以，因为，所以
所以
故答案为：
1．(2023·北京·人大附中三模）半径为的圆的边沿有一点，半径为的圆的边沿有一点，、两点重合后，小圆沿着大圆的边沿滚动，、两点再次重合小圆滚动的圈数为（ ）
A．B．C．D．
答案：D
【解析】设、两点再次重合小圆滚动的圈数为，则，其中、，
所以，，则当时，.
故、两点再次重合小圆滚动的圈数为.
故选：D.
2．(2023·湖北·房县第一中学模拟）已知圆台形的花盆的上、下底面的直径分别为8和6，该花盆的侧面展开图的扇环所对的圆心角为，则母线长为（ ）
A．4B．8C．10D．16
答案：A
【解析】如图，弧长为，弧长为，因为圆心角为，，，则母线.
故选：A.
3．(2023·广东·模拟）已知圆锥的全面积是底面积的3倍，那么这个圆锥的侧面积展开图-扇形的圆心角为（ ）
A．B．C．D．
答案：D
【解析】由题设，若圆锥底面半径为，母线长为，
∴由圆锥的全面积是底面积的3倍，则，即，
设圆锥的侧面积展开图-扇形的圆心角为，则，可得.
故选：D
4．(2023·浙江·高考真题）设，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件
答案：A
【解析】因为可得：
当时，，充分性成立；
当时，，必要性不成立；
所以当，是的充分不必要条件.
故选：A.
5．(2023·江苏·常州高级中学模拟）已知角的终边在直线上，则的值为（ ）
A．B．C．0D．
答案：C
【解析】由题知：
设角的终边上一点，则.
当时，，，，
.
当时，，，，
.
故选：C
6．(2023·辽宁实验中学模拟）已知，则_________．
答案：
【解析】
．
故答案为：．
7．(2023·山东·烟台二中模拟）已知，则______．
答案：0或1
【解析】由得：，
则，，所以或.
故答案为：0或1
8．(2023·山东威海·三模）已知，，则___________.
答案：
【解析】由题知：，
因为，所以.
故答案为：
9．(2023·湖北·荆州中学三模）若点关于轴对称点为，写出的一个取值为___．
答案：（满足即可）
【解析】与关于轴对称，
即关于轴对称，
，
则，
当时，可取的一个值为.
故答案为：（满足即可）.
10．(2023·广东深圳·二模）已知，则__________．
答案：
【解析】解：由题意可知： .
1．(2023·全国·高考真题（理））沈括的《梦溪笔谈》是中国古代科技史上的杰作，其中收录了计算圆弧长度的“会圆术”，如图，是以O为圆心，OA为半径的圆弧，C是AB的中点，D在上，．“会圆术”给出的弧长的近似值s的计算公式：．当时，（ ）
A．B．C．D．
答案：B
【解析】解：如图，连接，
因为是的中点，
所以，
又，所以三点共线，
即，
又，
所以，
则，故，
所以.
故选：B.
2．(2023·山东济南·二模）济南市洪家楼天主教堂于2006年5月被国务院列为全国重点文物保护单位.它是典型的哥特式建筑.哥特式建筑的特点之一就是窗门处使用尖拱造型，其结构是由两段不同圆心的圆弧组成的对称图形.如图2，和所在圆的圆心都在线段AB上，若，，则的长度为（ ）
A．B．C．D．
答案：A
【解析】过作，设圆弧AC的圆心为O，半径为，则，
在中，，所以，，
所以在直角三角形中，，所以，所以，而，
所以，所以.
故选：A.
3．(2023·山东日照·一模）已知角的终边经过点，则角可以为（ ）
A．B．C．D．
答案：D
【解析】角的终边经过点，
是第四象限角，且，，
则．
故选：D
4．(2023·北京市第五中学三模）若点A（csθ，sinθ）与关于x轴对称，则θ的一个取值为___________.
答案：（答案不唯一）
【解析】解：因为A（csθ，sinθ）与均在单位圆上，
设圆与x轴交于P､Q两点，A在第二象限，B在第三象限，如图所示：
则∠AOP=θ，∠AOB=，
因为A､B关于x轴对称，所以∠BOP=θ，
所以2θ+=2π，解得θ=，
则符合题意的θ的一个值可以为.
故答案为：（答案不唯一）.
.
5．(2023·浙江绍兴·模拟）勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线，它由德国机械工程专家，机构运动学家勒洛首先发现，其作法是：以等边三角形每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，三段弧围成的曲边三角形就是勒洛三角形．已知等边三角形的边长为1，则勒洛三角形的面积是_______．
答案：
【解析】由题意得，勒洛三角形的面积为：三个圆心角和半径均分别为和1的扇形面积之和减去两个边长为1的等边三角形的面积，
即．
故答案为：．
6．(2023·广东广东·一模）数学中处处存在着美，机械学家莱洛发现的莱洛三角形就给人以对称的美感．莱洛三角形的画法：先画等边三角形ABC，再分别以点A、B、C为圆心，线段AB长为半径画圆弧，便得到莱洛三角（如图所示）．若莱洛三角形的周长为，则其面积是______．
答案：
【解析】由条件可知，弧长，等边三角形的边长，则以点A、B、C为圆心，圆弧所对的扇形面积为，中间等边的面积

所以莱洛三角形的面积是.
故答案为：
7．(2023·上海市实验学校模拟）在中， 所对边分别为，若，则____________.
答案：.
【解析】由正弦定理可得，故，
通分得到，.
因为，所以，故即.
因为，故，填.
8．(2023·北京·101中学模拟）如图，单位圆Q的圆心初始位置在点（0，1），圆上一点P的初始位置在原点，圆沿x轴正方向滚动．当点P第一次滚动到最高点时，点P的坐标为______；当圆心Q位于点（3，1）时，点P的坐标为______．
答案：
【解析】由题意，作辅助图形，如图所示，
当点P第一次滚动到最高点时，点P向右滚动了圆的半个周长，因此点P的坐标为；
当圆心Q位于（3，1）时，此时圆心角为3，点P的横坐标为，
纵坐标为，所以点P的坐标为.
故答案为，．