

还剩3页未读,
继续阅读
初中数学13.2.2 用坐标表示轴对称教案及反思
展开
这是一份初中数学13.2.2 用坐标表示轴对称教案及反思,共6页。教案主要包含了情境引入,教学建议,对应训练,随堂训练,课堂总结,知识结构,作业布置等内容,欢迎下载使用。
解题大招一 由点的坐标关系列方程求解
例1 在平面直角坐标系中,点A(m+1,5)与点B(3,n)关于y轴对称,则m,n的值分别为( A )
A.m=-4,n=5 B.m=-4,n=3 C.m=2,n=5 D.m=-2,n=5
解析:∵点A(m+1,5)与点B(3,n)关于y轴对称,∴m+1=-3,n=5.∴m=-4,n=5.故选A.
解题大招二 根据特殊图形的对称性求坐标
例2 如图,分别以长方形ABCD的两条对称轴为x轴和y轴建立平面直角坐标系,若点A的坐标为(-4,3),写出长方形ABCD另外三个顶点的坐标.
分析:
解:B(-4,-3),C(4,-3),D(4,3).
培优点一 在平面直角坐标系中寻找轴对称变换的规律
例1 如图,在平面直角坐标系中,对△ABC 进行循环往复的轴对称变换,若原来点A的坐标是(2,5),则经过第2 025次变换后点A的对应点的坐标为( C )
A.(2,-5) B.(-2,-5) C.(-2,5) D.(2,5)
解析:观察轴对称变换可得,△ABC经过四次轴对称变换回到原始位置.∵点A的坐标是(2,5),∴第1次变换:点A的坐标为(-2,5);第2次变换:点A的坐标为(-2,-5);第3次变换:点A的坐标为(2,-5);第4次变换:点A的坐标为(2,5).∵2 025÷4=506……1,∴第2 025次变换后点A的坐标与第1次变换后相同,即为(-2,5).故选C.
培优点二 关于非坐标轴对称的点的坐标关系
例2 如图,在平面直角坐标系中,已知点A(-4,1),B(-4,5),C(-1,3).
(1)在图中作出△ABC关于直线m(直线m上各点的横坐标都为1)对称的图形△A1B1C1;
(2)线段BC上有一点P(-eq \f(5,2),4),直接写出点P关于直线m对称的点的坐标;
(3)线段BC上有一点M(a,b),若点M和点M′(c,d)关于直线m对称,请直接
写出a,b,c,d满足的数量关系.
分析:(1)首先确定A,B,C三点关于直线m的对称点,再顺次连接即可;
(2)(3)对称轴是任何一对对称点所连线段的垂直平分线,据此求解.
解:(1)如图,△A1B1C1即为所求.
(2)由轴对称的性质可得,点P与其对称点到直线m的距离相等,不难得出,点P关于直线m对称的点的横坐标为2-(-eq \f(5,2))=eq \f(9,2),纵坐标为4,∴点P关于直线m对称的点的坐标是(eq \f(9,2),4).
(3)由轴对称的性质知b=d,eq \f(1,2)(a+c)=1,即a+c=2,∴a,b,c,d满足的数量关系是a+c=2,b=d.
教学目标
课题
13.2 第2课时 用坐标表示轴对称
授课人
素养目标
1.掌握点或图形的轴对称变换引起的点的坐标的变化规律,能利用这种变化规律在平面直角坐标系中作出一个图形的轴对称图形.
2.通过总结轴对称变换引起的点的坐标变化规律,培养观察、归纳能力.
教学重点
1.在平面直角坐标系中关于x轴、y轴对称的点的坐标变化规律.
2.利用坐标变化规律在平面直角坐标系中作一个图形的轴对称图形.
教学难点
找对称点之间的坐标关系的规律.
教学活动
教学步骤
师生活动
活动一:创设情境,引入新知
设计意图
借助实际生活中的对称位置引入课题.
【情境引入】
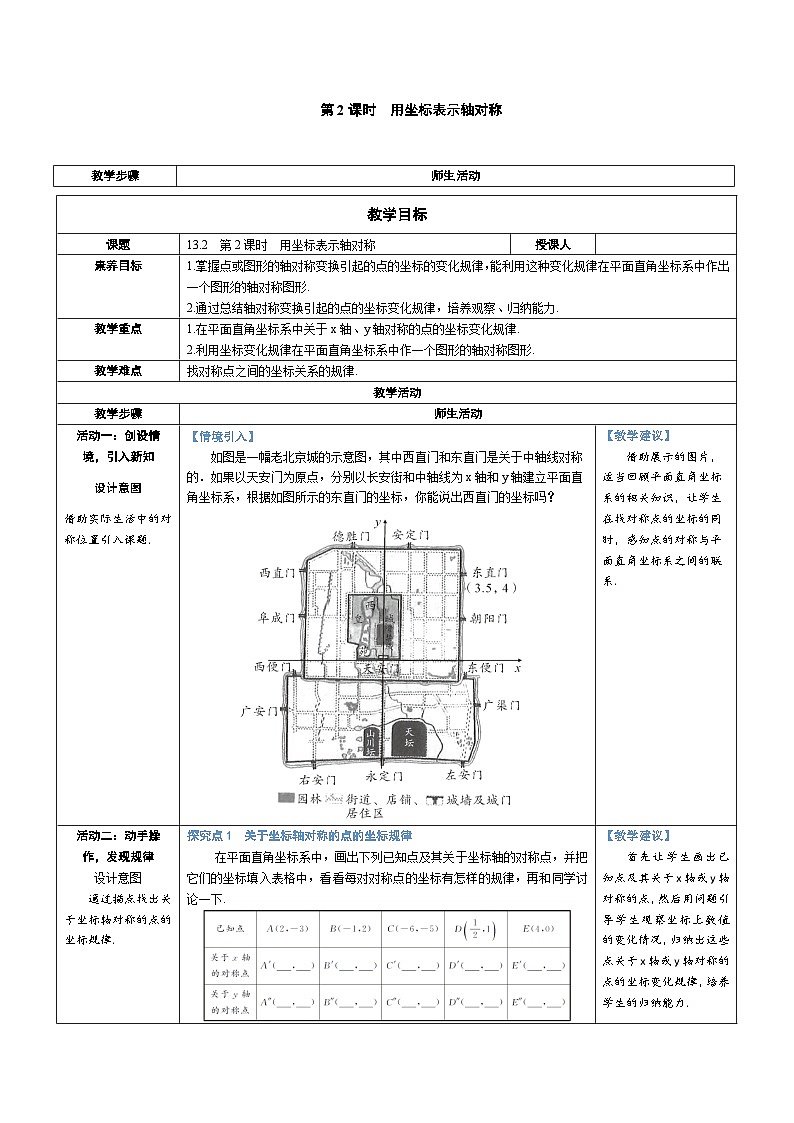
如图是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
【教学建议】
借助展示的图片,适当回顾平面直角坐标系的相关知识,让学生在找对称点的坐标的同时,感知点的对称与平面直角坐标系之间的联系.
活动二:动手操作,发现规律
设计意图
通过描点找出关于坐标轴对称的点的坐标规律.
探究点1 关于坐标轴对称的点的坐标规律
在平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律,再和同学讨论一下.
【教学建议】
首先让学生画出已知点及其关于x轴或y轴对称的点,然后用问题引导学生观察坐标上数值的变化情况,归纳出这些点关于x轴或y轴对称的点的坐标变化规律,培养学生的归纳能力.
教学步骤
师生活动
描点、填表如下.
问题1 关于x轴对称的两点,它们的横坐标有什么关系?纵坐标有什么关系?
它们的横坐标相同,纵坐标互为相反数.
问题2 关于y轴对称的两点,它们的横坐标有什么关系?纵坐标有什么关系?
它们的横坐标互为相反数,纵坐标相同.
归纳 点(x,y)关于 x 轴对称的点的坐标为(x,-y);
点(x,y)关于 y 轴对称的点的坐标为(-x,y).
简记:横轴对称,横不变纵变;纵轴对称,纵不变横变.
【对应训练】1.教材P70练习第1,2题.
2.点(4,3)与点(4,-3)的关系是( B )
A.关于原点对称 B.关于x轴对称
C.关于y轴对称 D.不能构成对称关系
教学中,要注意留给学生足够的空间,使学生活动起来,通过探究发现并总结规律.对于这些规律,不要让学生死记硬背,要让学生结合实例理解这些规律,尤其要特别关注学生对对称点的坐标的求解过程.
设计意图
根据对称点的坐标规律绘制轴对称图形,体会数与形的结合.
探究点2 绘制关于坐标轴对称的图形
如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),分别画出与四边形ABCD关于 y 轴和 x 轴对称的图形.
问题1 四边形ABCD的顶点A,B,C,D关于y轴对称的点分别为A′(5,1),B′(2,1),C′(2,5),D′(5,4).
【教学建议】
本例解答中有留白,教师让学生根据学过的规律自己写出对称点的坐标,自己画出对称的图形等,最后教师引导学生总结在平面直角坐标系中画轴对称图形的步骤.整个探究过程教师应注意让学生参与到解决问题的过程中去.
教学步骤
师生活动
问题2 画出四边形ABCD关于y轴对称的图形.
解:如图,四边形A′B′C′D′即为所求.
问题3 四边形ABCD的顶点A,B,C,D关于x轴对称的点分别为A″(-5,-1),B″(-2,-1),C″(-2,-5),D″(-5,-4).
问题4 画出四边形ABCD关于x轴对称的图形.
解:如图,四边形A″B″C″D″即为所求.
总结:在平面直角坐标系中画轴对称图形的步骤.
【对应训练】
教材P71练习第3题.
活动三:知识升华,巩固提升
设计意图
加深对对称点的坐标规律的理解.
例 如图,在△ABC中,A,B,C三点的坐标分别为A(3,-2),B(1,-4),C(5,-5).
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)请直接写出△A1B1C1三个顶点的坐标;
(3)求△ABC的面积.
解:(1)如图,△A1B1C1即为所求.
(2)由图可得,A1(3,2),B1(1,4),C1(5,5).
(3)△ABC的面积为4×3-eq \f(1,2)×4×1-eq \f(1,2)×2×2-eq \f(1,2)×2×3=5
【教学建议】
在网格中求三角形的面积时,可先补一个长方形,再用面积的和差求解.
【对应训练】
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-3,-2).
(1)请在图中作出△ABC关于y轴对称的图形△DEF(点D,E,F分别与点A,B,C对应);
(2)直接写出D,E,F三点的坐标;
(3)求△DEF的面积.
解:(1)如图,△DEF即为所求.
(2)D(-2,3),E(-3,1),F(3,-2).
(3)S△DEF=6×5-12×1×2-12×5×5-12×3×6=7.5.
活动四:随堂训练,课堂总结
【随堂训练】见《创优作业》“随堂小练”册子相应课时随堂训练.
【课堂总结】师生一起回顾本节课所学主要内容,并请学生回答以下问题:
1.关于x轴对称的点的坐标规律是怎样的?
2.关于y轴对称的点的坐标规律是怎样的?
3.如何在平面直角坐标系中,绘制出某个图形关于坐标轴对称的图形?
【知识结构】
【作业布置】
1.教材P71习题13.2第2,3,4,5,6,7题.
2.《创优作业》主体本部分相应课时训练.
板书设计
第2课时 用坐标表示轴对称
1.关于坐标轴对称的点的坐标规律.
2.绘制关于坐标轴对称的图形.
教学反思
本节课先总结关于坐标轴对称的点的坐标规律,再据此绘制关于坐标轴对称的图形,让学生体会了轴对称变换中的数形结合.今后的教学中可多运用这种数学思想,给学生的数学学习增添新工具.
解题大招一 由点的坐标关系列方程求解
例1 在平面直角坐标系中,点A(m+1,5)与点B(3,n)关于y轴对称,则m,n的值分别为( A )
A.m=-4,n=5 B.m=-4,n=3 C.m=2,n=5 D.m=-2,n=5
解析:∵点A(m+1,5)与点B(3,n)关于y轴对称,∴m+1=-3,n=5.∴m=-4,n=5.故选A.
解题大招二 根据特殊图形的对称性求坐标
例2 如图,分别以长方形ABCD的两条对称轴为x轴和y轴建立平面直角坐标系,若点A的坐标为(-4,3),写出长方形ABCD另外三个顶点的坐标.
分析:
解:B(-4,-3),C(4,-3),D(4,3).
培优点一 在平面直角坐标系中寻找轴对称变换的规律
例1 如图,在平面直角坐标系中,对△ABC 进行循环往复的轴对称变换,若原来点A的坐标是(2,5),则经过第2 025次变换后点A的对应点的坐标为( C )
A.(2,-5) B.(-2,-5) C.(-2,5) D.(2,5)
解析:观察轴对称变换可得,△ABC经过四次轴对称变换回到原始位置.∵点A的坐标是(2,5),∴第1次变换:点A的坐标为(-2,5);第2次变换:点A的坐标为(-2,-5);第3次变换:点A的坐标为(2,-5);第4次变换:点A的坐标为(2,5).∵2 025÷4=506……1,∴第2 025次变换后点A的坐标与第1次变换后相同,即为(-2,5).故选C.
培优点二 关于非坐标轴对称的点的坐标关系
例2 如图,在平面直角坐标系中,已知点A(-4,1),B(-4,5),C(-1,3).
(1)在图中作出△ABC关于直线m(直线m上各点的横坐标都为1)对称的图形△A1B1C1;
(2)线段BC上有一点P(-eq \f(5,2),4),直接写出点P关于直线m对称的点的坐标;
(3)线段BC上有一点M(a,b),若点M和点M′(c,d)关于直线m对称,请直接
写出a,b,c,d满足的数量关系.
分析:(1)首先确定A,B,C三点关于直线m的对称点,再顺次连接即可;
(2)(3)对称轴是任何一对对称点所连线段的垂直平分线,据此求解.
解:(1)如图,△A1B1C1即为所求.
(2)由轴对称的性质可得,点P与其对称点到直线m的距离相等,不难得出,点P关于直线m对称的点的横坐标为2-(-eq \f(5,2))=eq \f(9,2),纵坐标为4,∴点P关于直线m对称的点的坐标是(eq \f(9,2),4).
(3)由轴对称的性质知b=d,eq \f(1,2)(a+c)=1,即a+c=2,∴a,b,c,d满足的数量关系是a+c=2,b=d.
教学目标
课题
13.2 第2课时 用坐标表示轴对称
授课人
素养目标
1.掌握点或图形的轴对称变换引起的点的坐标的变化规律,能利用这种变化规律在平面直角坐标系中作出一个图形的轴对称图形.
2.通过总结轴对称变换引起的点的坐标变化规律,培养观察、归纳能力.
教学重点
1.在平面直角坐标系中关于x轴、y轴对称的点的坐标变化规律.
2.利用坐标变化规律在平面直角坐标系中作一个图形的轴对称图形.
教学难点
找对称点之间的坐标关系的规律.
教学活动
教学步骤
师生活动
活动一:创设情境,引入新知
设计意图
借助实际生活中的对称位置引入课题.
【情境引入】
如图是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
【教学建议】
借助展示的图片,适当回顾平面直角坐标系的相关知识,让学生在找对称点的坐标的同时,感知点的对称与平面直角坐标系之间的联系.
活动二:动手操作,发现规律
设计意图
通过描点找出关于坐标轴对称的点的坐标规律.
探究点1 关于坐标轴对称的点的坐标规律
在平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律,再和同学讨论一下.
【教学建议】
首先让学生画出已知点及其关于x轴或y轴对称的点,然后用问题引导学生观察坐标上数值的变化情况,归纳出这些点关于x轴或y轴对称的点的坐标变化规律,培养学生的归纳能力.
教学步骤
师生活动
描点、填表如下.
问题1 关于x轴对称的两点,它们的横坐标有什么关系?纵坐标有什么关系?
它们的横坐标相同,纵坐标互为相反数.
问题2 关于y轴对称的两点,它们的横坐标有什么关系?纵坐标有什么关系?
它们的横坐标互为相反数,纵坐标相同.
归纳 点(x,y)关于 x 轴对称的点的坐标为(x,-y);
点(x,y)关于 y 轴对称的点的坐标为(-x,y).
简记:横轴对称,横不变纵变;纵轴对称,纵不变横变.
【对应训练】1.教材P70练习第1,2题.
2.点(4,3)与点(4,-3)的关系是( B )
A.关于原点对称 B.关于x轴对称
C.关于y轴对称 D.不能构成对称关系
教学中,要注意留给学生足够的空间,使学生活动起来,通过探究发现并总结规律.对于这些规律,不要让学生死记硬背,要让学生结合实例理解这些规律,尤其要特别关注学生对对称点的坐标的求解过程.
设计意图
根据对称点的坐标规律绘制轴对称图形,体会数与形的结合.
探究点2 绘制关于坐标轴对称的图形
如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),分别画出与四边形ABCD关于 y 轴和 x 轴对称的图形.
问题1 四边形ABCD的顶点A,B,C,D关于y轴对称的点分别为A′(5,1),B′(2,1),C′(2,5),D′(5,4).
【教学建议】
本例解答中有留白,教师让学生根据学过的规律自己写出对称点的坐标,自己画出对称的图形等,最后教师引导学生总结在平面直角坐标系中画轴对称图形的步骤.整个探究过程教师应注意让学生参与到解决问题的过程中去.
教学步骤
师生活动
问题2 画出四边形ABCD关于y轴对称的图形.
解:如图,四边形A′B′C′D′即为所求.
问题3 四边形ABCD的顶点A,B,C,D关于x轴对称的点分别为A″(-5,-1),B″(-2,-1),C″(-2,-5),D″(-5,-4).
问题4 画出四边形ABCD关于x轴对称的图形.
解:如图,四边形A″B″C″D″即为所求.
总结:在平面直角坐标系中画轴对称图形的步骤.
【对应训练】
教材P71练习第3题.
活动三:知识升华,巩固提升
设计意图
加深对对称点的坐标规律的理解.
例 如图,在△ABC中,A,B,C三点的坐标分别为A(3,-2),B(1,-4),C(5,-5).
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)请直接写出△A1B1C1三个顶点的坐标;
(3)求△ABC的面积.
解:(1)如图,△A1B1C1即为所求.
(2)由图可得,A1(3,2),B1(1,4),C1(5,5).
(3)△ABC的面积为4×3-eq \f(1,2)×4×1-eq \f(1,2)×2×2-eq \f(1,2)×2×3=5
【教学建议】
在网格中求三角形的面积时,可先补一个长方形,再用面积的和差求解.
【对应训练】
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-3,-2).
(1)请在图中作出△ABC关于y轴对称的图形△DEF(点D,E,F分别与点A,B,C对应);
(2)直接写出D,E,F三点的坐标;
(3)求△DEF的面积.
解:(1)如图,△DEF即为所求.
(2)D(-2,3),E(-3,1),F(3,-2).
(3)S△DEF=6×5-12×1×2-12×5×5-12×3×6=7.5.
活动四:随堂训练,课堂总结
【随堂训练】见《创优作业》“随堂小练”册子相应课时随堂训练.
【课堂总结】师生一起回顾本节课所学主要内容,并请学生回答以下问题:
1.关于x轴对称的点的坐标规律是怎样的?
2.关于y轴对称的点的坐标规律是怎样的?
3.如何在平面直角坐标系中,绘制出某个图形关于坐标轴对称的图形?
【知识结构】
【作业布置】
1.教材P71习题13.2第2,3,4,5,6,7题.
2.《创优作业》主体本部分相应课时训练.
板书设计
第2课时 用坐标表示轴对称
1.关于坐标轴对称的点的坐标规律.
2.绘制关于坐标轴对称的图形.
教学反思
本节课先总结关于坐标轴对称的点的坐标规律,再据此绘制关于坐标轴对称的图形,让学生体会了轴对称变换中的数形结合.今后的教学中可多运用这种数学思想,给学生的数学学习增添新工具.