







初中数学沪科版九年级下册25.2.2 由三视图确定几何体及计算优质课件ppt
展开能够利用三视图的相关知识解决实际问题;能够通过简单的三视图还原立体图形本身,并解决面积、体积等问题;通过解决实际问题,培养学生的应用意识;4. 经历由“三视图”想象出立体几何图形本身的过程,培养学生分析问题、解决问题的能力.
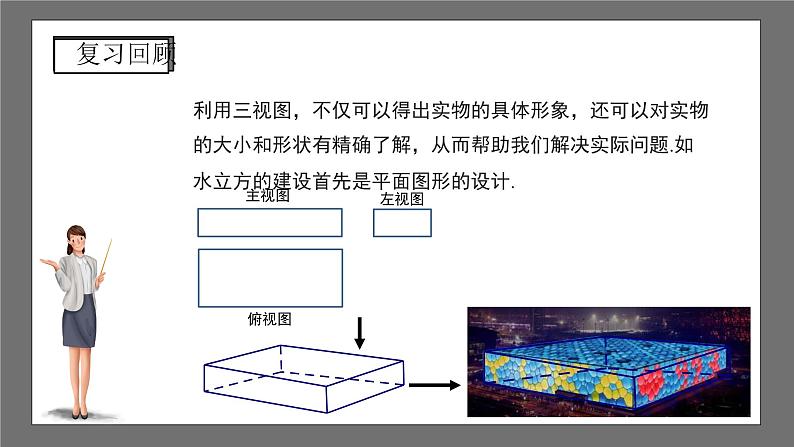
利用三视图,不仅可以得出实物的具体形象,还可以对实物的大小和形状有精确了解,从而帮助我们解决实际问题.如 水立方的建设首先是平面图形的设计.
现在要做一个模具,它的三视图如下图,你能计算一下它的体积吗?
思路引导:先根据三视图还原实物,再根据体积公式计算出体积即可
结论:上面是一个圆柱,高为32,底面直径是20下面是一个长方体,高为40,长30,宽25
除了体积的计算问题,我们还需要进行表面积的计算问题,解决方法是一致的,根据三视图还原几何体的长、宽、高等,根据计算公式进行计算即可.
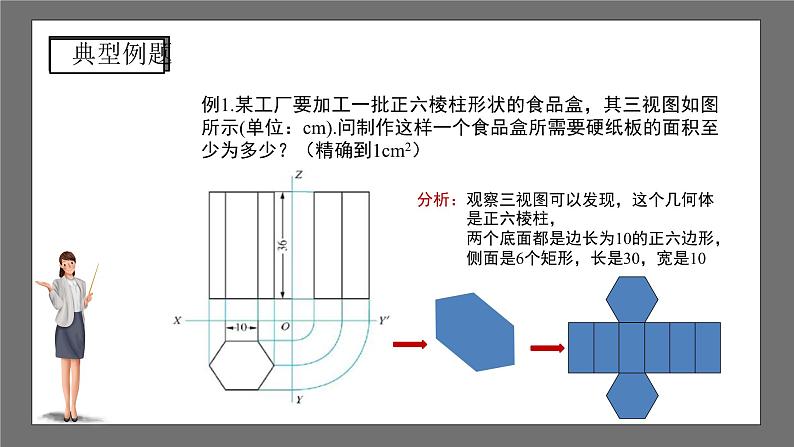
例1.某工厂要加工一批正六棱柱形状的食品盒,其三视图如图所示(单位:cm).问制作这样一个食品盒所需要硬纸板的面积至少为多少?(精确到1cm2)
分析:观察三视图可以发现,这个几何体 是正六棱柱, 两个底面都是边长为10的正六边形, 侧面是6个矩形,长是30,宽是10
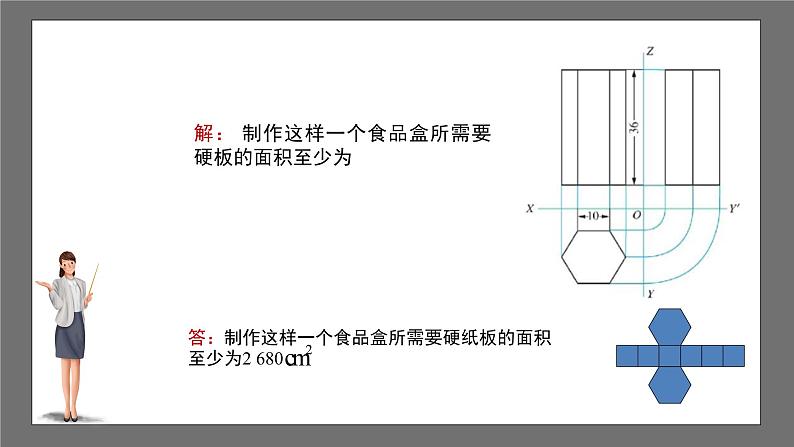
解: 制作这样一个食品盒所需要硬板的面积至少为
例2.一个几何体的三视图如图所示,求这个这个几何体的表面积.
分析:由三视图可知该几何体为 两个长方体的组合体,如图
解:主视图的面积=10×60+50×20=1 600, 左视图的面积=40×(50+10)=2 400 俯视图的面积=40×(20+20+20)=2 400,∴这个几何体的表面积=2×(1 600+2 400+2 400)=12 800.
1.如图,是下列哪个几何体的主视图与俯视图( )
2.如图是一个几何体的三视图(尺寸单位:cm),根据图中所示数据求得这个几何体的侧面积是( )A.12 cm2B.(12+π)cm2C.6π cm2D.8π cm2
3. 一个几何体的三视图如图所示,则该几何体的表面积是( )A.24+2πB.16+4πC.16+8πD.16+12π
当组合体是由上、下两个四棱柱组成时,表面积就是三个视图的面积和的2倍
三视图在面积体积中的应用
注意:实际问题中计算表面积时,需要确定是否加上底面的面积
(1)由三视图想象出立体图形(2)确定立体图形的高、底面的长与宽或者直接(3)根据公式,计算表面积与体积
初中数学沪科版九年级下册25.2.1 简单几何体的三视图及其画法优质课件ppt: 这是一份初中数学沪科版九年级下册<a href="/sx/tb_c102914_t3/?tag_id=26" target="_blank">25.2.1 简单几何体的三视图及其画法优质课件ppt</a>,文件包含沪科版数学九年级下册252《三视图》第1课时课件pptx、沪科版数学九年级下册252《三视图》第1课时教案doc等2份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
数学25.2.1 简单几何体的三视图及其画法课文内容课件ppt: 这是一份数学25.2.1 简单几何体的三视图及其画法课文内容课件ppt,文件包含252第1课时三视图及其画法pptx、252第1课时三视图及其画法docx等2份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
数学九年级下册第25章 投影与视图25.2 三视图25.2.1 简单几何体的三视图及其画法备课ppt课件: 这是一份数学九年级下册第25章 投影与视图25.2 三视图25.2.1 简单几何体的三视图及其画法备课ppt课件,共8页。PPT课件主要包含了H水平面,W侧面,V正面,三视图的形成,随堂小测等内容,欢迎下载使用。













