江苏省南京市秦淮区2023-2024学年八年级下学期期末数学试卷

这是一份江苏省南京市秦淮区2023-2024学年八年级下学期期末数学试卷，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

八年级数学
注意事项：
本试卷共6页.全卷满分 100分.考试时间为100分钟.考生答题全部答在答题卡上，答在本试卷上无效.
一、选择题(本大题共6小题，每小题2分，共12分.在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的序号填涂在答题卡相应位置上)
1. 2024年南京市有67011名初中毕业生参加升学考试，为了了解这67011 名考生的数学成绩，从中抽取2000名考生的数学成绩进行统计，在这个问题中样本是 ( )
A. 67011名考生 B. 抽取的2000名考生
C. 67011 名考生的数学成绩 D. 抽取的2000名考生的数学成绩
2. 与 19最接近的整数是
A. 3 B. 4 C. 5 D. 6
3.在若m≠n，则下列化简一定正确的是( )
A.m+3n+3=mn B.m-3n-3=mn C.m3n3=mn D.3m3n=mn
4. 点A (x₁, y₁) , B (x₂, y₂) 在反比例函数 y=kxk≠0的图像上，下列说法正确的是
A.若x₁y₂
C. 若. x₁+x₂=0,,则y₁+y₂=0 D. 若 x₁⋅x₂=1,则. y₁⋅y₂=1
5. 如图，在▱ABCD中，对角线AC、BD相交于点O，下列条件中，不能判断这个平行四边形是菱形的是
A. ∠BAC=∠ABD B. AB=AD C. ∠BAC=∠DAC D. AC⊥BD
6.如图，显示了某次用计算机模拟随机投掷一枚图钉的实验结果.下面有三个推断：
①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；②随着试验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；③若再次用计算机模拟此实验，则当投掷次数为1000时，“钉尖向上”的频率一定是0.620. 其中合理的是
A. ① B. ② C. ①② D. ①③
第 1 页 共 6 页
二、填空题(本大题共10小题，每小题2分，共20分.不需写出解答过程，请把答案直接填写在答题卡相应位置上)
7.一个不透明的袋中装有3个红球，2个黄球，1 个白球，每个球除颜色外都相同.从袋中任意摸出一球，则摸到 ▲ 球的可能性最大. (填“红色”、 “黄色”或“白色”)
8. 计算: 8-13×6的 ▲ .
9.若式子 1+x+1-x在实数范围内有意义，则x的取值范围是 ▲ .
10.某种油菜籽在相同条件下发芽试验的结果如下：
这种油菜籽发芽的概率的估计值是 ▲ . (结果精确到0.01)
11.如图,在平面直角坐标系中,菱形 OABC的顶点A的坐标是(3,1).若顶点 B 在第一象限的角平分线上，则点B的坐标是 ▲ .
12.如图，在方格纸中，线段AB绕某个点旋转一定角度得到线段CD，其中点A的对应点是点C,则旋转中心是点 ▲ .
13. 当m= ▲ 时, 关于x的分式方程 2x+mx-3=-1无解.
14. 对于函数 y=2x,当y<1时,x的取值范围是 ▲ .
15. 如图, 在▱ABCD中, ∠ABC, ∠BCD的平分线分别交AD于点E, F. 若AB=a, CF=b,则BE的长为 ▲ . (用含a,b的代数式表示)
16.如图,在平面直角坐标系中,正方形 ABCD 如此摆放,点A的坐标为(一1,0),点B 的坐标为(0,2),点D在反比例函数 y=kxk≠0上.将正方形沿x轴正方向平移m个单位长度后，点 C恰好落在该函数图象上，则m的值是 ▲ .
第 2 页 共 6 页
每批粒数
50
100
300
400
600
1000
发芽的频数
45
96
283
380
571
948
三、解答题(本大题共10小题，共68分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤)
17. (6分) 计算:
1212-313×6; 2a-ca-b-c-bb-a.
18. (6分) 解分式方程:
13x+1=6x-1; 21-xx-2=12-x-2.
19. (4分)我们都知道，数学来源于生活，生活中处处有数学.例如：现有a克糖水，其中含有b克糖 (a>b>0)，则糖水的浓度(即糖的质量与糖水的质量比)是b/a，生活经验告诉我们，在糖水中加水，糖水会变淡.请运用所学知识证明这一道理.
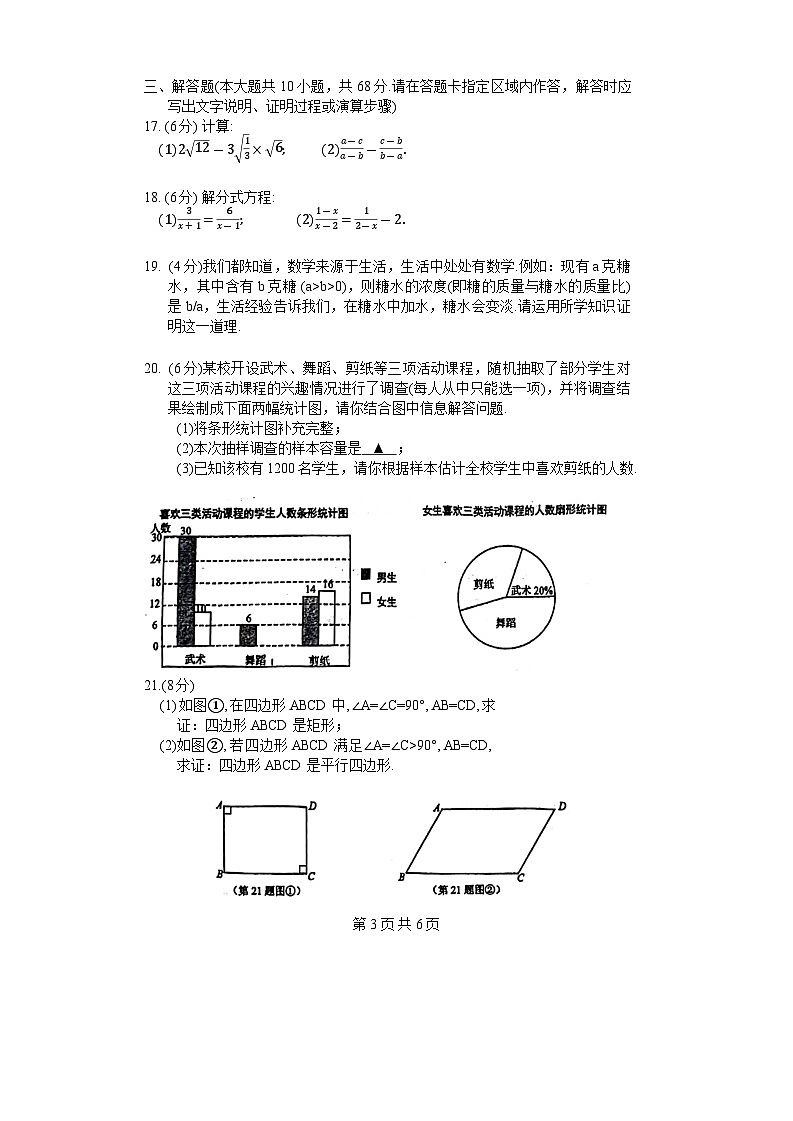
20. (6分)某校开设武术、舞蹈、剪纸等三项活动课程，随机抽取了部分学生对这三项活动课程的兴趣情况进行了调查(每人从中只能选一项)，并将调查结果绘制成下面两幅统计图，请你结合图中信息解答问题.
(1)将条形统计图补充完整；
(2)本次抽样调查的样本容量是 ▲ ；
(3)已知该校有1200名学生，请你根据样本估计全校学生中喜欢剪纸的人数.
21.(8分)
(1) 如图①, 在四边形ABCD中, ∠A=∠C=90°, AB=CD,求证：四边形ABCD是矩形；
(2)如图②, 若四边形ABCD满足∠A=∠C>90°, AB=CD,求证：四边形ABCD是平行四边形.
第 3 页 共 6 页
22. (6分)已知∠MAN，按要求完成下列尺规作图(不写作法，保留作图痕迹)：
(1) 如图①, B、C分别在射线AM、AN上,, 求作□ABDC;
(2) 如图②, 点O是∠MAN内一点, 求作线段PQ, 使P、Q分别在射线AM、AN上,且点O是PQ的中点.
23. (6分)某中学组织学生去离学校15千米的农场，先遣队比大队提前20分钟出发，先遣队的速度是大队速度的1.2倍，结果先遣队比大队早到0.5小时.先遣队和大队的速度各是多少?
24. (8分)图①、图②是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上.
(1)如图①，点P、M在小正方形的顶点上，在图①中作出点P关于点M的对称点Q，连接AQ、QC、CP、PA, 则四边形AQCP的周长为 ▲ ;
(2) 在图②中画出一个以线段AC为对角线，面积为6的矩形ABCD，且点B和点D均在小正方形的顶点上.
第 4 页 共 6 页
25. (8分) 平行的思考.
【作平行】
(1)如图①，过P作l₂∥AB. (限用圆规和没有刻度的直尺，保留作图痕迹，不必写出作法和理由)
【折平行】
现有一张长方形纸片ABCD，小明和小丽分别折平行线.
小明：如图②，折出 BD，展平后再折叠纸片，使点A、C分别落在BD所在直线上的点A'、C'处, 展平纸片, 得到折痕BM、DN.
小丽: 如图③, 将边MC折至MC'处, 再将边AD折至AD'处, 使得MC'和A'D'在一条直线上,展平纸片,得到折痕MN、EF.
【证平行】
(2) 小明发现BM∥DN，小丽发现MN∥EF. 请你选择其中一个发现进行证明.(选择小明的，全部正确得3分；选择小丽的，全部正确得5分).
第 5 页 共 6 页
26. (10分)对于两个不同的函数，通过减法运算可以得到一个新函数，我们把这个新函数称为两个函数的“差函数”.例如：对于函数y₁=3x和y₂=x-1, 则函数y₁, y₂的“差函数”记为y₃=y₁-y₂=3x- (x-1) =2x+1.
(1) 已知函数y₁=x³和 y2=1x,若将这两个函数的“差函数”记为y3；
①写出y₃的表达式, y₃= ;
②函数y₁，y₂的图象如图①所示，则y₃的大致图象是 ；
(2)已知函数:y₄=x+1和 y5=1x+1,若将这两个函数的“差函数”记为y6，判断下列关于“差函数”，y₀描述的正确性，并对正确的描述进行证明：
A.y₆的图象与x轴没有公共点；
B. y6的图象关于 (一1, 0)对称;
C. 当x<-1时, y₆随x的值增大而减小;
D. 当x>-1时, 随着x的值增大, y₆的图象越来越接近y₄=x+1 的图象.上述描述正确的为 ；
第 6 页 共 6 页