甘肃省兰州市榆中县多校联考2024届九年级下学期中考二模数学试卷(含答案)

这是一份甘肃省兰州市榆中县多校联考2024届九年级下学期中考二模数学试卷(含答案)，共26页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．我国古代数学名著《九章算术》中对正负数的概念注有“今两算得失相反,要令正负以名之”、如：粮库把运进30吨粮食记为“”,则“”表示( )
A.运出30吨粮食B.亏损30吨粮食C.卖掉30吨粮食D.吃掉30吨粮食
2．杆秤是中国最古老也是现今人们仍然使用的衡量工具,由秤杆、秤砣、秤盘三个部分组成.秤砣、秤杆分别叫做“权”和“衡”,指的是做任何事都要权衡轻重.如图是常见的一种秤砣,则它的主视图是( )
A.B.C.D.
3．下列式子运算正确的是( )
A.B.C.D.
4．某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中,都与地面l平行,,.当为( )度时,与平行.
A.16B.60C.66D.114
5．一次函数的函数值y随x的增大而减小,则k的取值范围( )
A.B.C.D.
6．若,是方程两个根,则( )
A.B.C.D.
7．如图,线段上的点C满足关系式：,且,则的长为( )
A.或B.C.D.
8．如图,是一个底部呈球形的蒸馏瓶,球的半径为,瓶内液体的最大深度,则截面圆中弦的长为( )
A.B.C.D.
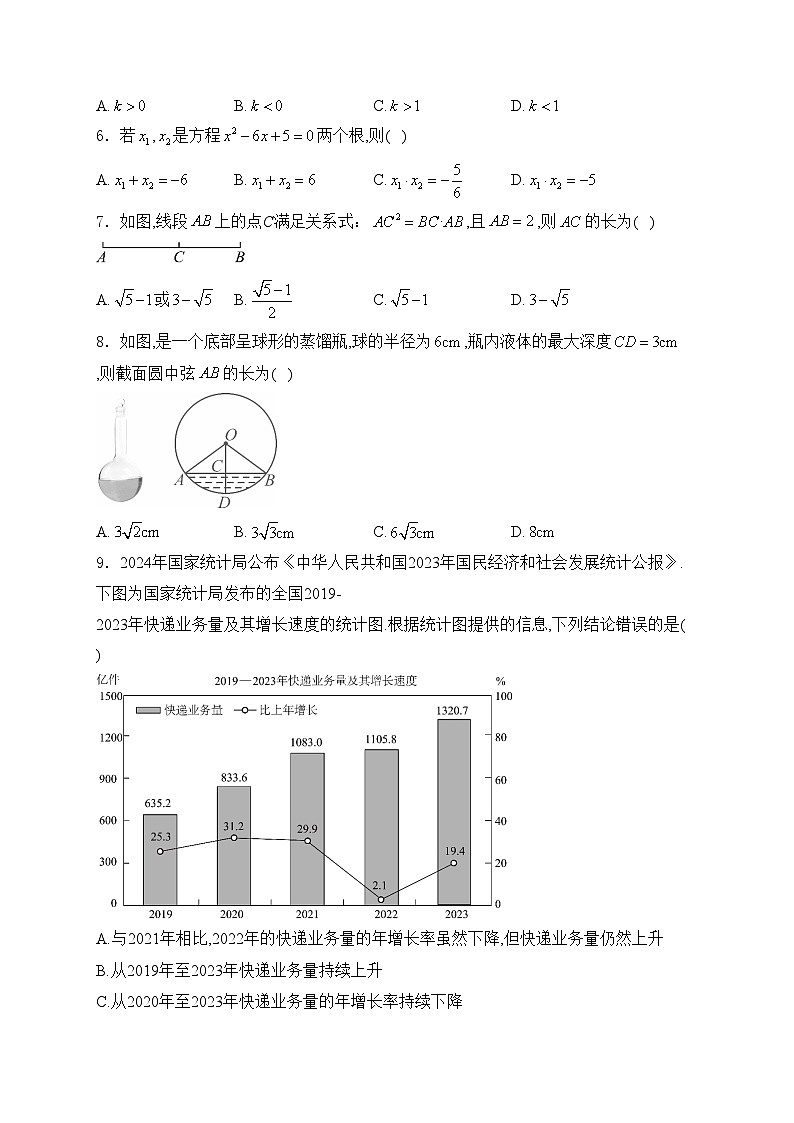
9．2024年国家统计局公布《中华人民共和国2023年国民经济和社会发展统计公报》.下图为国家统计局发布的全国2019-2023年快递业务量及其增长速度的统计图.根据统计图提供的信息,下列结论错误的是( )
A.与2021年相比,2022年的快递业务量的年增长率虽然下降,但快递业务量仍然上升
B.从2019年至2023年快递业务量持续上升
C.从2020年至2023年快递业务量的年增长率持续下降
D.2023年的快递业务量比2022年增加了214.9亿件
10．《四元玉鉴》是一部成就辉煌的数学名著,在中国古代数学史上有着重要地位.其中有一个“酒分醇醨”问题：务中听得语吟吟,亩道醇醨酒二盆.醇酒一升醉三客,醨酒三升醉一人.共通饮了一斗七,一十九客醉醺醺.欲问高明能算士,几何醨酒几多醇？其大意为：有好酒和薄酒分别装在瓶中,好酒1升醉了3位客人,薄酒3升醉了1位客人,现在好酒和薄酒一共饮了17升,醉了19位客人,试问好酒、薄酒各有多少升？若设好酒有x升,薄酒有y升,根据题意列方程组为( )
A.B.C.D.
11．如图,把含30°的直角三角板PMN放置在正方形ABCD中,,直角顶点P在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,且点O为MN的中点,则的度数为( )
A.60°B.65°C.75°D.80°
12．如图,等边的边长为,点P从点A出发,以的速度沿向点C运动,到达点C停止；同时点Q从点A出发,以的速度沿向点C运动,到达点C停止,设的面积为,运动时间为,则下列最能反映y与x之间函数关系的图象是( )
A.B.
C.D.
二、填空题
13．今年春季以来,甘肃天水麻辣烫成为美食界和旅游圈的“顶流”,持续火爆“出圈”,不仅吸引了无数游客和美食博主前往打卡,也带动了当地的消费.各大短视频平台上,“甘肃麻辣烫”相关话题累计播放量已超过3260000000次,数据3260000000用科学记数法可表示为________.
14．因式分解：__.
15．为了培养同学们的创新精神和实践能力,某校组织学生开展了为期一周的社会实践活动.学校开设了A.“皮影戏”,B.“香包绣制”,C.“甘肃勇纸”,D.“洮砚制作技艺”四门实践课程供学生选择,且每人只能参加一门实践课程.甲、乙两位同学各自从这四门实践课程中随机选一门,他们选择的实践课程相同的概率为________.
16．在平面直角坐标系中,矩形的边BC在x轴上,O为线段的中点,矩形的顶点,连接,按照下列方法作图：
(1)以点C为圆心,适当的长度为半径画弧分别交,于点E,F；
(2)分别以点E,F为圆心,大于的长为半径画弧交于点G；
(3)作射线交于H,则线段的长为_______.
三、解答题
17．解不等式：.
18．计算：.
19．化简：.
20．作图题：
(1)画图并思考：(不写作法,说明知识原理)
如图,某村庄计划把河中的水引到水池M中,怎样开渠线路最短,画出图形；其数学原理是_______________________________.
(2)尺规作图：(不写作法,保留作图痕迹)
已知：和如下图所示,画出.
21．一次函数的图象与反比例函数的图象交于点,两点.
(1)求反比例函数的解析式及一次函数的解析式；
(2)求的面积.
22．“逐梦寰宇问苍穹——中国载人航天工程三十年成就展”的成功举办,标志着我国载人航天工程正式进入空间站应用与发展阶段.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取m名学生进行测试,并对成绩(满分：100分)进行整理、描述和分析,将成绩划分为,,,四个等级,并绘制出下列不完整的统计图.
其中B等级的成绩数据(单位:分)∶80,86,80,82,85,88,86,89,81,86.
根据以上信息,回答下列问题.
(1)抽取的总人数_____,并补全条形统计图.
(2)在所抽取的m名学生的测试成绩中,中位数是_____分,B等级的众数是_____分.
(3)若该中学共有3000名学生,且全部参加这次测试,请估计学生的测试成绩不低于80分的总人数.
23．如图，在菱形ABCD中，O为AC，BD的交点，P，M，N分别为CD，OD，OC的中点.
（1）求证：四边形OMPN是矩形，
（2）连接AP，若，，求AP的长.
24．古树名木是中华民族悠久历史与文化的象征.据悉,在兰州树龄1000年以上古树仅有4棵,分别为七里河区工人文化宫两棵唐槐(树龄约1320年),红古区张家寺村寺庙旁文成槐(树龄约1300年),榆中县定远镇矿湾村龙泉寺旁圆柏(树龄约1000年).某数学兴趣小组开展测量工人文化宫其中一棵唐槐高度的“数学综合与实践”活动,测量实践报告如下表：
根据以上表中的测量方案及其数据,计算唐槐的高度(结果保留整数).
25．掷实心球是中考体育考试项目之一,明明发现实心球从出手到落地的过程中,实心球竖直高度与水平距离一直在相应的发生变化.明明利用先进的鹰眼系统记录了实心球在空中运动时的水平距离x(单位：米)与竖直高度y(单位：米)的数据如表：
根据表中的数据建立如图所示的平面直角坐标系,根据图中点的分布情况,明明发现其图象是二次函数的一部分.
(1)求满足条件的抛物线的解析式；
(2)根据中考体育考试评分标准(男生版),在投掷过程中,实心球从起点到落地点的水平距离大于或等于9.7米时,即可得满分10分,明明在此次考试中是否得到满分,请说明理由.
26．如图,是的直径,垂直与过点C的切线,交与于D,连接.
(1)求证：平分；
(2)若的半径为2,,求劣弧的长度.
27．综合探究
综合与实践课上,智慧星小组三位同学对含角的菱形进行了探究.
背景在菱形中,,作,,分别交边,于点P,Q.
(1)感知如图1,若点P是边的中点,小智经过探索发现了线段与之间的数量关系,请你直接写出这个关系为________.
(2)探究如图2,当点P为上任意一点时,请说明(1)中的结论是否仍然成立,并写出理由.
(3)应用若菱形纸片中,,,在边上取一点P,连接,在菱形内部作,交于点Q,当时,请直接写出线段的长.
28．对于平面直角坐标系中的点P和(半径为r),给出如下定义：若点P关于点M的对称点为Q,且,则称点P为的称心点.
(1)当⊙O的半径为2时,
①如图1,在点,,中,的称心点是；
②如图2,点D在直线上,若点D是的称心点,求点D的横坐标m的取值范围；
(2)的圆心为,半径为2,直线与x轴,y轴分别交于点E,F.若线段上的所有点都是的称心点,直接写出t的取值范围.
参考答案
1．答案：A
解析：粮库把运进30吨粮食记为“”,则“”表示运出30吨粮食.
故选：A.
2．答案：A
解析：这个常见的一种秤砣的主视图如下：
故选A.
3．答案：C
解析：A、,故此选项不符合题意；
B、,故此选项不符合题意；
C、,故此选项符合题意；
D、,故此选项不符合题意；
故选：C.
4．答案：C
解析：∵,都与地面l平行,
∴,
∴,
∴,
∵,,
∴,
∴当时,.
故选：C.
5．答案：D
解析：∵一次函数的函数值y随x的增大而减小,
∴,
解得.
故选：D.
6．答案：B
解析：∵,是方程两个根,
∴,.
故选：B.
7．答案：C
解析：设,则,
∵,
∴,
整理得,,
解得,或(不符合题意,舍去)
∴,
故选：C.
8．答案：C
解析：由题意得：,
∴,,
∵,,
∴,
在中,由勾股定理得：,
∴.
∴截面圆中弦AB的长为.
故选：C.
9．答案：C
解析：由统计图可知：
与2021年相比,2022年的快递业务量的年增长率虽然下降,但快递业务量仍然上升,故选项A说法正确,不符合题意；
从2019年至2023年快递业务量持续上升,故选项B说法正确,不符合题意；
从2020年至2022年快递业务量的年增长率持续下降,从2022年至2023年快递业务量的年增长率有所上升,故选项C说法错误,符合题意；
(亿件),即2023年的快递业务量比2022年增加了214.9亿件,故选项D说法正确,不符合题意.
故选：C.
10．答案：A
解析：根据好酒1升醉了3位客人,薄酒3升醉了1位客人,现在好酒和薄酒一共饮了17升,醉了19位客人,列出方程组得：
故选：A.
11．答案：C
解析：∵四边形ABCD是正方形中,
∴,
∵点O为MN的中点
∴,
∵,
∴,
∴,
∴,
∴,
,
故选：C.
12．答案：D
解析：由题得,点Q移动的路程为,点P移动的路程为x,
,,
①如图,当点Q在上运动时,过点Q作于D,
则,,,
∴的面积,
即当时,函数图象为开口向上的抛物线的一部分,故A、B排除；
②如图,当点Q在上运动时,过点Q作于E,
则,,,
∴的面积,
即当时,函数图象为开口向下的抛物线的一部分,故C排除,而D正确；
故选：D.
13．答案：
解析：,
故答案为：.
14．答案：
解析：原式.
故答案为：.
15．答案：
解析：列表如下：
由表格可知,一共有16种等可能性的结果数,其中他们选择的实践课程相同的结果数有4种,
∴他们选择的实践课程相同的概率为,
故答案为：.
16．答案：/1.5
解析：如图,过点H作于点M,
由作法可知,为的平分线,
∵四边形为矩形,
∴,,
∴,
∵,
∴,,
由勾股定理得,,
∵,
∴,即,
解得,
故答案为：.
17．答案：
解析：,
去分母,得,
移项,得,
合并同类项,得,
不等式的两边都除以,得.
18．答案：
解析：
.
19．答案：
解析：
.
20．答案：(1)垂线段最短
(2)图见解析
解析：(1)直线外一点与直线上各点连接的所有线段中,垂线段最短或“垂线段最短”.
∴如图,即为所求的最短线路.
(2)如图所示：即为所求.
.
21．答案：(1),
(2)的面积为
解析：(1)将点代入,得：,
解得：,
则反比例函数解析式为：；
将点代入,得：,
将点A、B的坐标代入一次函数解析式,得：,
解得：,
故一次函数解析式为：.
(2)一次函数解析式为：,
令,则,
∴点C的坐标为,
∴,
∴.
22．答案：(1)50
(2)85.5,86
(3)1800名
解析：(1)人,
等级C的人数：(人),
补全条形统计图如图：
故答案为:50.
(2)把B等级数据按从小到大排列为80,80,81,82,85,86,86,86,88.89,
中间两个数是85、86,
∴中位数是；
在这组数据里86分的最多,
∴众数为86,
故答案为:85.5,86.
(3)名,
答：估计学生的测试成绩不低于80分的总人数为1800名.
23．答案：（1）证明见解析
（2）
解析：（1）P，M，N分别为CD，OD，OC的中点，
，是的中位线，
，，
四边形OMPN是平行四边形，
四边形ABCD是菱形，
，，
四边形OMPN是矩形.
（2）如图，四边形ABCD是菱形，
，，，，
，是等边三角形，
，.
在中，由勾股定理，得..
M，N分别为OD，OC的中点，
，，
.
由（1）可知，四边形OMPN是矩形，
，，
在中，.
24．答案：唐槐的高度约为
解析：由题意得,,,,,
设,
在中,,
,
,
在中,,
解得,
经检验,是原方程的解且符合题意,
.
唐槐的高度约为.
25．答案：(1)
(2)明明在此次考试中能得到满分,理由见解析
解析：(1)由题意,根据表格的数据可得对称轴是直线,
∴顶点为.
故可设抛物线的解析式为,
把代入,
得,
∴.
∴抛物线的解析式为.
(2)明明在此次考试中能得到满分,理由如下：
把代入,
得,
解得或(不符合题意,舍去),
∵,
∴明明在此次考试中能得到满分.
26．答案：(1)证明见解析
(2)
解析：(1)证明：连接,
∵与相切于点C,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴平分；
(2)连接,
∵是的直径,
∴,
∴,
∵,
∴,
∴,
∴,
∴或(舍去),
在中,,
∴,
∴,
∵,
∴是等边三角形,
∴,
∴劣弧的长度,
∴劣弧的长度为.
27．答案：(1)
(2)成立；理由见解析
(3)线段的长为5或3
解析：(1)线段与之间的数量关系：.
理由：如图,连接,
四边形是菱形,且,
,,
和都是等边三角形,
,,
点P是边的中点,
,,
,
,
,
,
,
,
在和中,
,
,
故答案为：.
(2)证明：成立.理由：
如图,连接,
四边形是菱形,且,
,,
和都是等边三角形,
,,,
,
,
,
,
在和中,
,
,
.
(3)如图,过点A作于E,连接,
四边形是菱形,且,,
,
是等边三角形,
,
,
,
,
当点P在点E的左侧时,,
当点P在点E的右侧(图中处)时,,
或,
由(2)知：,
,
或3.
线段的长为5或3.
28．答案：(1)①点A,B；②点D的横坐标m的取值范围是或
(2)或
解析：(1)①∵,
∴点A关于点O的对称点为,
∴,
∵的半径为2,
∴点A是的称心点,
∵,
∴点B关于点O的对称点为,
∴,
∵的半径为2,
∴,
∴点B是的称心点,
∵,
∴点C关于点O的对称点为,
∴,
∴点C不是的称心点,
故答案为：点A,B；
②∵点D在直线上,且点D的横坐标为m,
∴D的坐标为,
∴点D关于点O的对称点的坐标为,
∴,
∵点D是的称心点,且的半径为2,
∴,
∴或,
∴点D的横坐标m的取值范围是或；
(2)如图,
对于直线,令,
∴,
∴,
∴,
令,
∴,
∴,
∴,
∴,
在中,,
∴,
过y轴上一点H作直线的垂线交线段于G,
∵线段上的所有点都是的称心点,且的半径为2,
∴,
在中,,
∴,
∴,
当点T从H向下移动时,,,越来越长,直到点G和E重合,取最大值,
∵线段上的所有点都是的称心点,
∴,
∴,
∴,
∴,
∴,
∴,
当点T从点H向上移动时,点T在上时,T到的距离小于2,此种情况不符合题意,
当点T从点F向上移动时,,
即：,
∵线段上的所有点都是的称心点,
∴,,
∴,,
∴,
且t的取值范围是或.
活动课题
测量唐槐()高度(唐槐有围栏保护,测量小组无法到达其底部)
活动目的
运用三角函数知识解决实际问题
测量工具
自制测倾器、皮尺等
方案示意图
测量步骤
(1)利用测倾器站在F处,测得唐槐最高点A的仰角为；
(2)前进6米到达D处,测得A点的仰角为.
说明
、为测倾器的支杆,在测量过程中、、唐槐均与水平面垂直,且D、F、B共线.
测量数据
,,米,米
参考数据
,,
水平距离x/m
0
2
4
5
6
8
竖直高度y/m
2
3.2
36
3.5
3.2
2
A
B
C
D
A
B
C
D