


























沪教版 (五四制)八年级下册22.3 特殊的平行四边形优秀ppt课件
展开1.经历矩形、菱形判定定理的探究过程,掌握菱形的判 定定理.(重点) 2.会用这些矩形、菱形的判定方法进行有关的证明和计算. (难点)
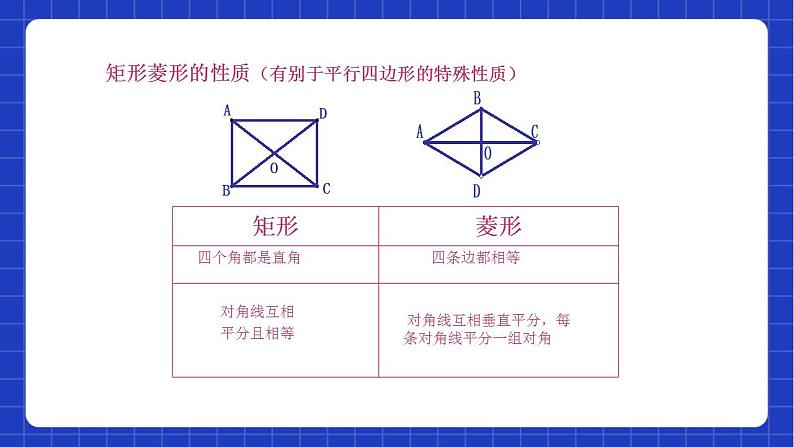
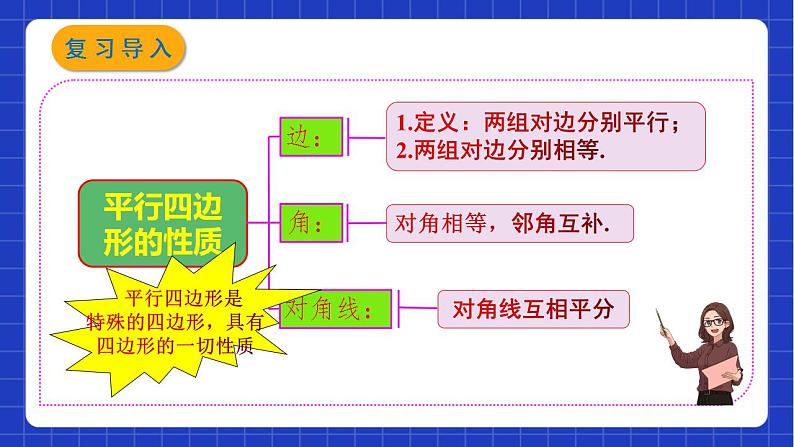
矩形菱形的性质(有别于平行四边形的特殊性质)
对角线互相垂直平分,每条对角线平分一组对角
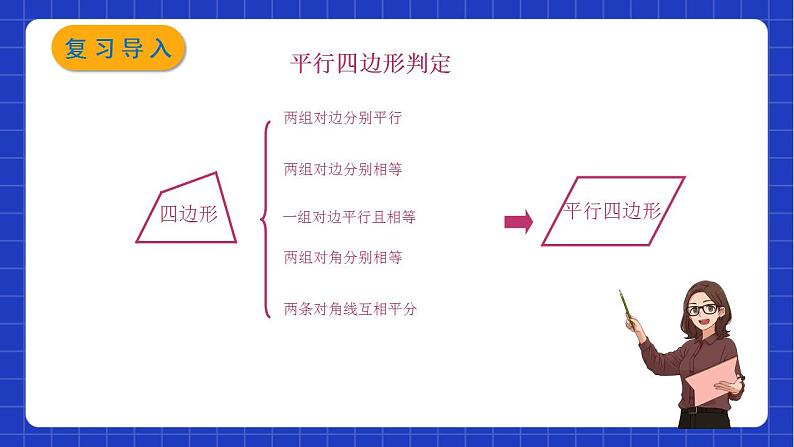
思考矩形和菱形具有一些特殊的性质,是否能从它们的性质定理所揭示的图形特征中,找到判定矩形和菱形的简捷、有效的方法?1.对于四边形 ABCD,从它的角或边进行考察.
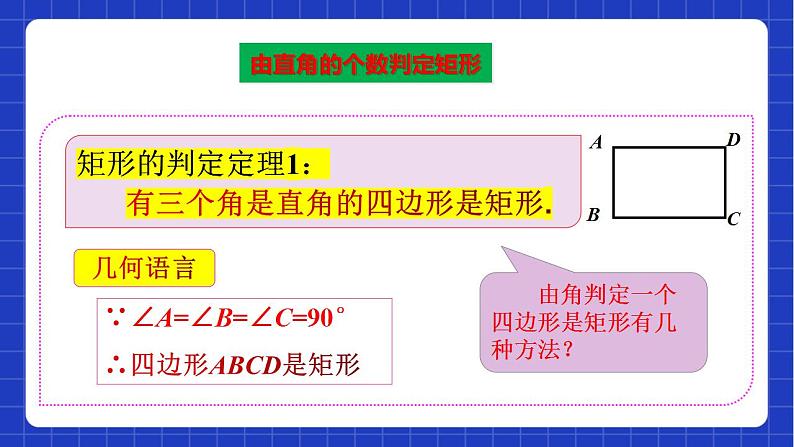
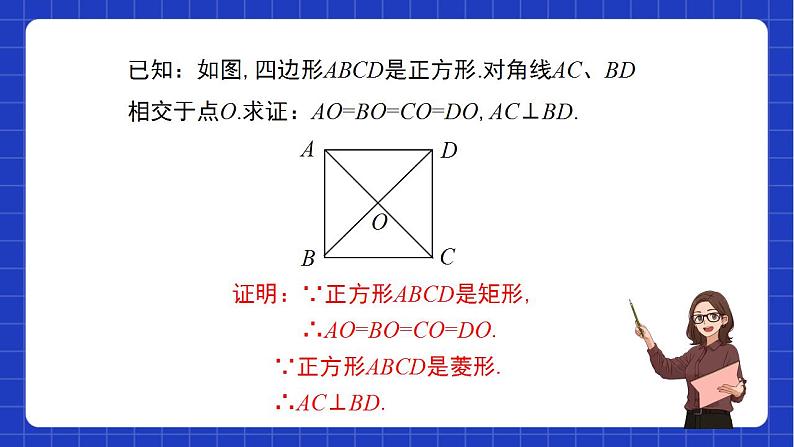
已知:如图所示,在四边形ABCD中, ∠A=∠B=∠C=90°. 求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=90°, ∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC, AB∥CD.∴四边形ABCD是平行四边形.
∵∠A=90°.∴□ ABCD是矩形.
矩形的判定定理1: 有三个角是直角的四边形是矩形.
∵∠A=∠B=∠C=90°∴四边形ABCD是矩形
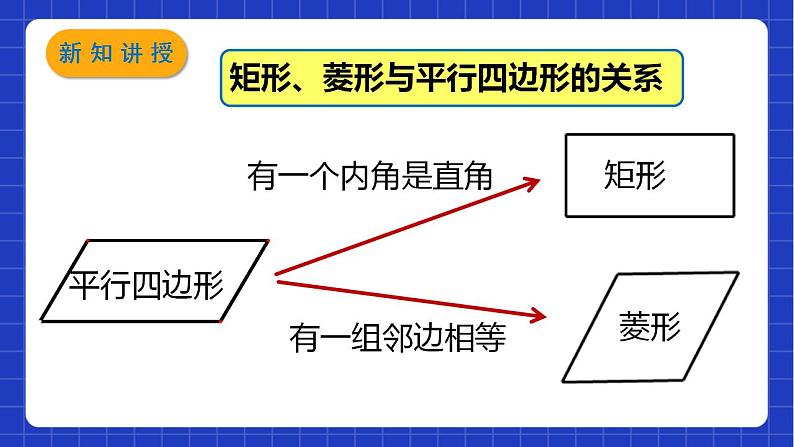
由角判定一个四边形是矩形有几种方法?
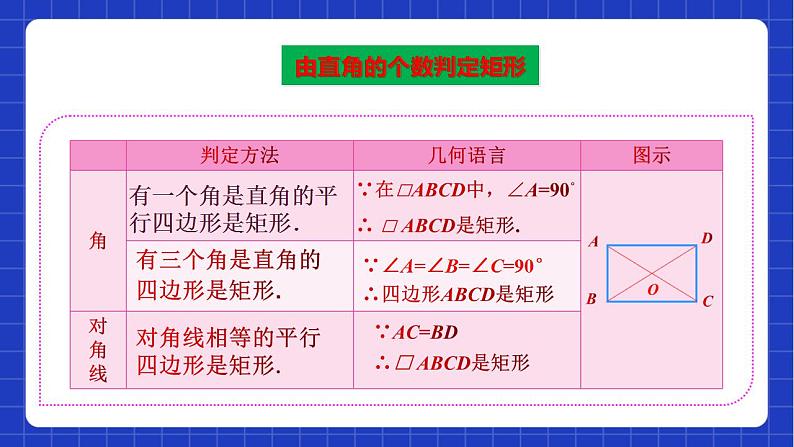
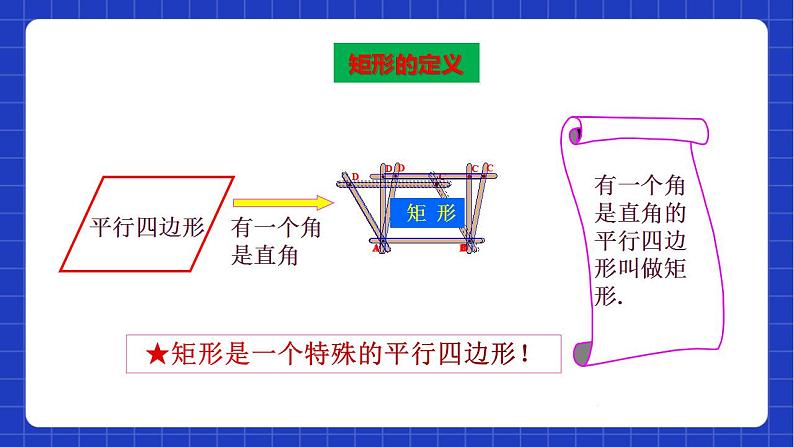
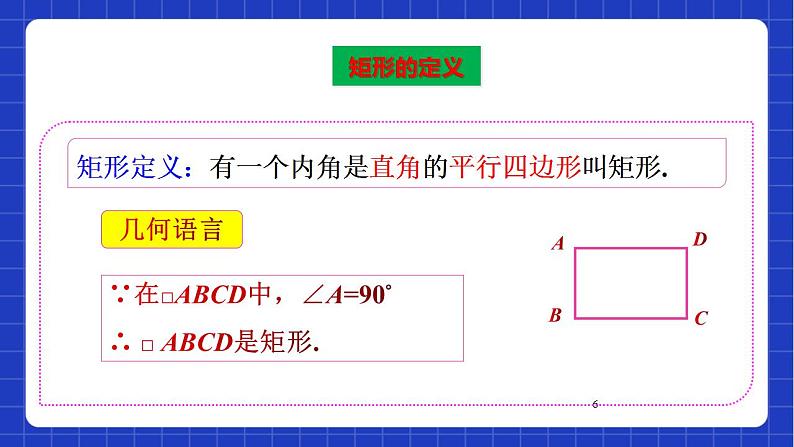
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
对角线相等的平行四边形是矩形.
∵AC=BD∴□ ABCD是矩形
∵在□ABCD中,∠A=90°∴ □ ABCD是矩形.
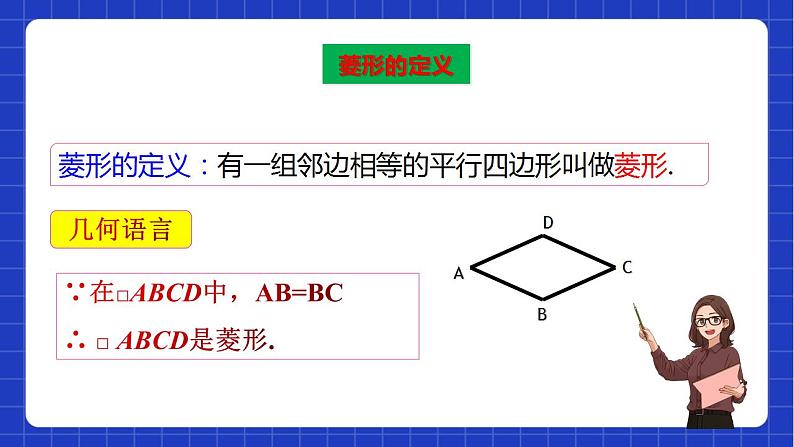
菱形的判定定理1:四边都相等的四边形是菱形.
证明:在四边形ABCD中 ∵AB=CD,BC=AD ∴四边形ABCD是平行四边形 ∵AB=BC ∴平行四边形ABCD是菱形
如果□ABCD 的两条对角线相等,即AC=BD,那么可以推出△DAB≌△CBA,得∠DAB= ∠ CBA又由 AD//BC,可知∠DAB+∠CBA=180°,得∠DAB=90°所以, □ ABCD 是矩形
2.在四边形 ABCD 是平行四边形的基础上,从它的对角线进行考察.
矩形的判定定理2: 对角线相等的平行四边形是矩形.
由对角线的关系判定矩形
两条对角线相等的四边形不一定是矩形,这个四边形必须是平行四边形才可以.
用对角线相等的平行四边形是矩形判定一个四边形是矩形必须满足两个条件:一是对角线相等,二是四边形是平行四边形.
菱形的判定定理2:对角线互相垂直的平行四边形是菱形.
证明:∵四边形ABCD是平行四边形 ∴AO=OC ∵AC ⊥ BD ∴∠AOB=∠COB=90° 又∵BO是公共边 ∴△AOB≌△COB ∴AB=BC
制作门窗或矩形零件时,在得到其两组对边分别相等后,可通过测量两条对角线长度来检验四个角是否符合要求,其依据是什么?
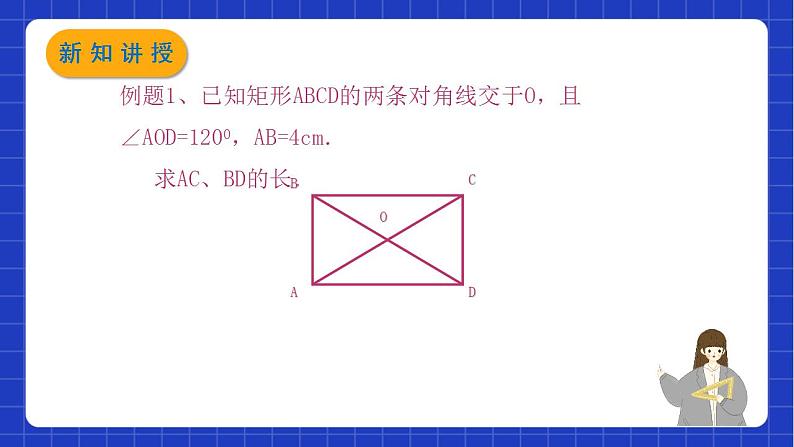
例题4 已知:如图22-39,矩形ABCD的对角线AC与BD相交于点 O,点 E、F、G、H 分别在 AO、BO、CO、DO 上,且AE=BF=CG=DH求证;四边形 EFGH 是矩形.
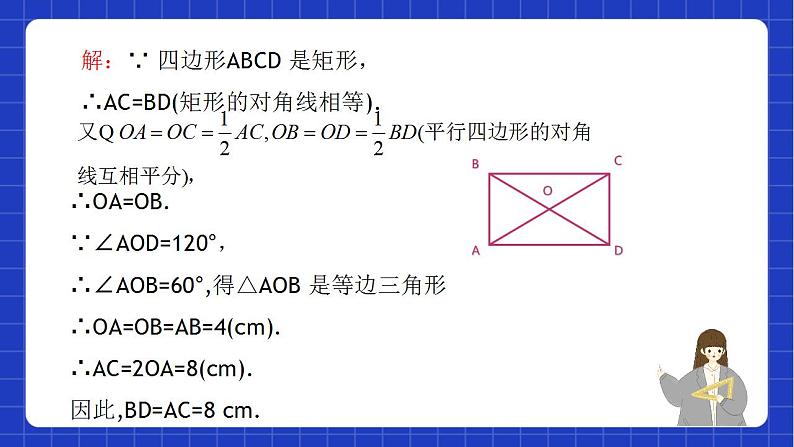
证明∵四边形ABCD 是矩形∴ AC=BD(矩形的对角线相等);得 AO=BO=CO=DO.由 AE=BF=CG=DH,得 OE-OF=OG=OH.∴四边形 EFGH 是平行四边形(对角线互相平分的四边形是平行四边形)∵EO+OG=FO+OH,即 EG=FH,∴四边形 EFGH 是矩形(对角线相等的平行四边形是矩形).
例题5 已知:如图 22-40,EF 是□ ABCD 的对角线AC的垂直平分线,EF 与边AD、BC 分别交于点 E、F求证:四边形AFCE 是蓉形。
例题5、已知:如图EF是□ABCD的对角线AC的垂直平分线,EF与边AD,BC分别交于点E,F. 求证:四边形AECF是菱形
分析 已知 EF⊥AC,所以要证明四边形 AFCE 是菱形,只要证明四边形 AFCE 是平行四边形.
证明 ∵四边形 ABCD 是平行四边形, ∴AE //FC(平行四边形的对边平行),得 ∠1= ∠ 2.∵EF 垂直平分AC,∴AO=OC, ∠ AOE= ∠ COF=90°∴△AOE≌△COF,得 EO=FO.
∴四边形 AFCE 是平行四边形(对角线互相平分的四边形是平行四边形).又∵ EF⊥AC,∴四边形 AFCE 是菱形(对角线互相垂直的平行四边形是菱形).
1. 如图,将一张矩形的纸片对折两次,沿虚线剪下,再打开,我们得到的是菱形吗? 为什么?
2.证明:对角线相等且互相平分的四边形是矩形.
3.如图,已知 BF、BE 分别是∠ABC 与它的邻补角的平分线AE⊥BE 于点 E,AF⊥BF 于点 F,那么四边形 AEBF 是矩形吗?为什么?
1、□ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
2.判断下列说法是否正确(1)对角线互相垂直的四边形是菱形;(2)对角线互相垂直且平分的四边形是菱形;(3)对角线互相垂直,且有一组邻边相等的 四边形是菱形;(4)两条邻边相等,且一条对角线平分一组 对角的四边形是菱形.
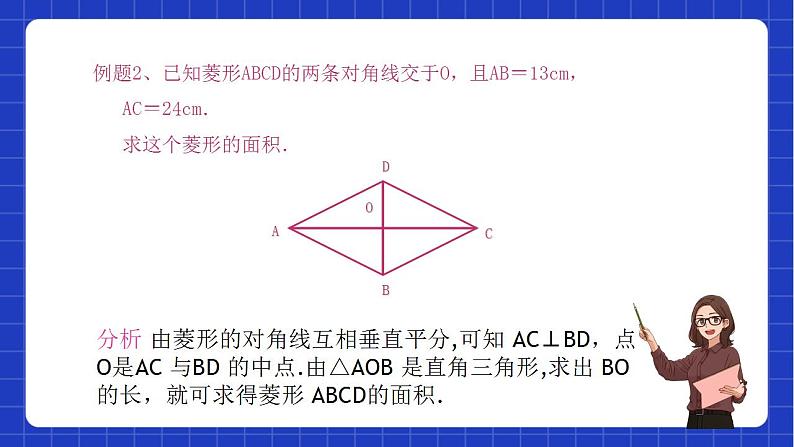
3.一边长为5cm平行四边形的两条对角线的长分别为 24cm和26cm,那么平行四边形的面积是 .
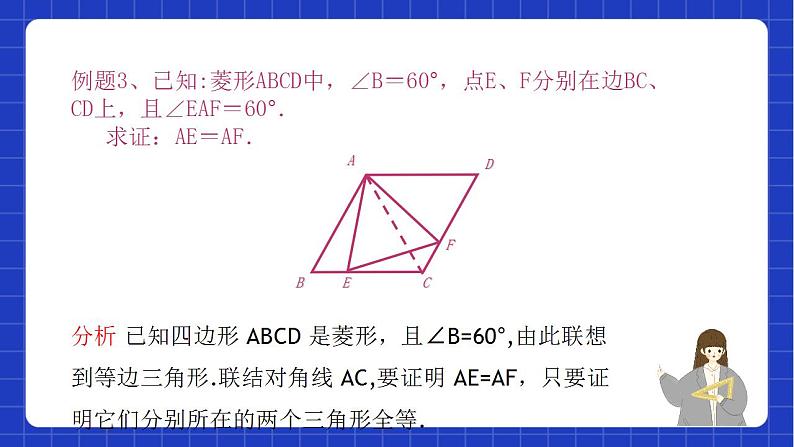
3.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( ) A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
解析:∵将△ABC沿BC方向平移得到△DCE,∴AC∥DE,AC=DE,∴四边形ABED为平行四边形.当AC=BC时,平行四边形ACED是菱形.故选B.
4.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( ) A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
5. 如图,在□ ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
解:∵四边形ABCD是平行四边形,∴OA=OC= AC,OB=OD= BD.
又 OA=OD,∴ AC=BD.∴四边形ABCD是矩形.∴ ∠DAB=90°.
又∠OAD=50°,∴∠OAB=40°.
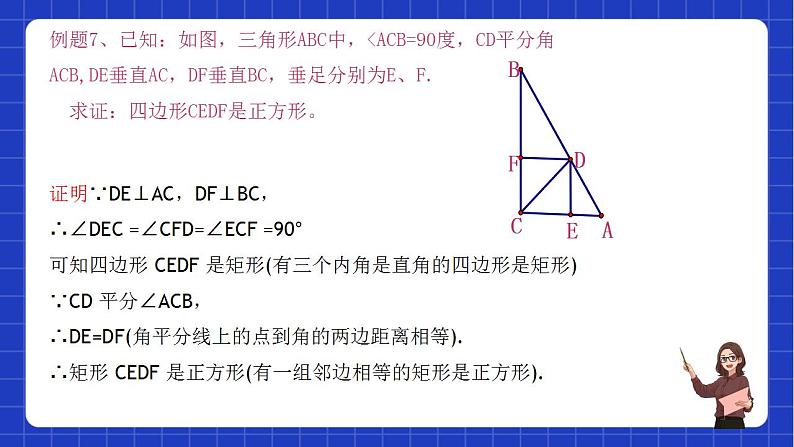
6. 如图,□ ABCD的四个内角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形.
证明:∵AB∥CD,∴∠ABC+∠BCD=180°.∵BG平分∠ABC,CG平分∠BCD,∴∠GBC+∠GCB= ∠ABC+ ∠BCD = ×180°=90°,∴∠BGC=90°. 同理可得∠AFB=∠AED=90°.∴∠GFE=∠FEH=∠FGH=90°.∴四边形EFGH是矩形.
7.如图,矩形ABCD的对角线相交于点O,BE∥AC,AE ∥BD.求证:四边形OAEB是菱形.
证明:∵DE∥AC,CE∥BD,∴四边形OAEB是平行四边形.∵四边形ABCD是矩形,∴OA=OB,∴四边形OCED是菱形.
8.如图,在平行四边形ABCD中,AC平分∠DAB,AB=3,求平行四边形ABCD的周长.
解:∵四边形ABCD为平行四边形,∴AD∥BC,AB∥CD,∴∠DAC=∠ACB,∠BAC=∠ACD,∵AC平分∠DAB,∴∠DAC=∠BAC,∴∠DAC=∠ACD,∴AD=DC,∴四边形ABCD为菱形,∴四边形ABCD的周长=4×3=12.
对角线互相垂直的平行四边形.
有一组邻边相等的平行四边形是菱形.
对角线互相垂直平分的四边形.
定义:有一个角是直角的平行四边形判定定理1:对角线相等的平行四边形
判定定理2:三个角是直角的四边形
初中数学沪教版 (五四制)八年级下册22.4 梯形优质课件ppt: 这是一份初中数学沪教版 (五四制)八年级下册<a href="/sx/tb_c43548_t3/?tag_id=26" target="_blank">22.4 梯形优质课件ppt</a>,文件包含沪教版数学八年级下册224《梯形》教学课件pptx、沪教版数学八年级下册224《梯形》分层练习原卷版docx、沪教版数学八年级下册224《梯形》分层练习解析版docx等3份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
初中数学沪教版 (五四制)八年级下册22.2 平行四边形优秀课件ppt: 这是一份初中数学沪教版 (五四制)八年级下册<a href="/sx/tb_c43546_t3/?tag_id=26" target="_blank">22.2 平行四边形优秀课件ppt</a>,文件包含沪教版数学八年级下册2224《平行八边形的判定》教学课件pptx、沪教版数学八年级下册2223《平行八边形的判定》教学课件pptx、沪教版数学八年级下册2221《平行八边形的性质》教学课件pptx、沪教版数学八年级下册2222《平行八边形的性质》教学课件pptx、沪教版数学八年级下册222《平行四边形》分层练习原卷版docx、沪教版数学八年级下册222《平行四边形》分层练习解析版docx等6份课件配套教学资源,其中PPT共56页, 欢迎下载使用。
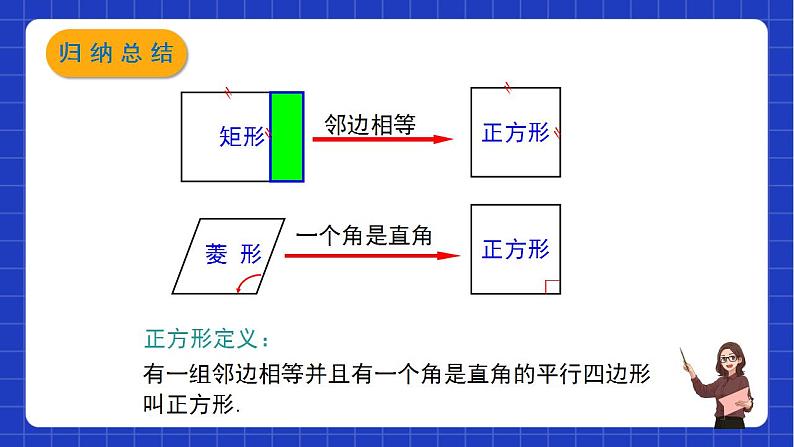
沪教版 (五四制)八年级下册22.3 特殊的平行四边形备课ppt课件: 这是一份沪教版 (五四制)八年级下册22.3 特殊的平行四边形备课ppt课件,共39页。PPT课件主要包含了正方形的性质等内容,欢迎下载使用。













