北师大版七年级数学下册第3章变量之间的关系单元测试(能力提升卷大)(原卷版+解析)

这是一份北师大版七年级数学下册第3章变量之间的关系单元测试(能力提升卷大)(原卷版+解析)，共20页。试卷主要包含了5kg时的售价．，4×2，9；7等内容，欢迎下载使用。

班级：___________________ 姓名：_________________ 得分：_______________
注意事项：
本试卷满分120分，试题共23题，其中选择10道、填空6道、解答7道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2023春•封丘县月考）一本数学错题笔记本的售价为6元，若小青买x本共付y元，则x和6分别是（ ）
A．常量，变量B．变量，常量C．常量，常量D．变量，变量
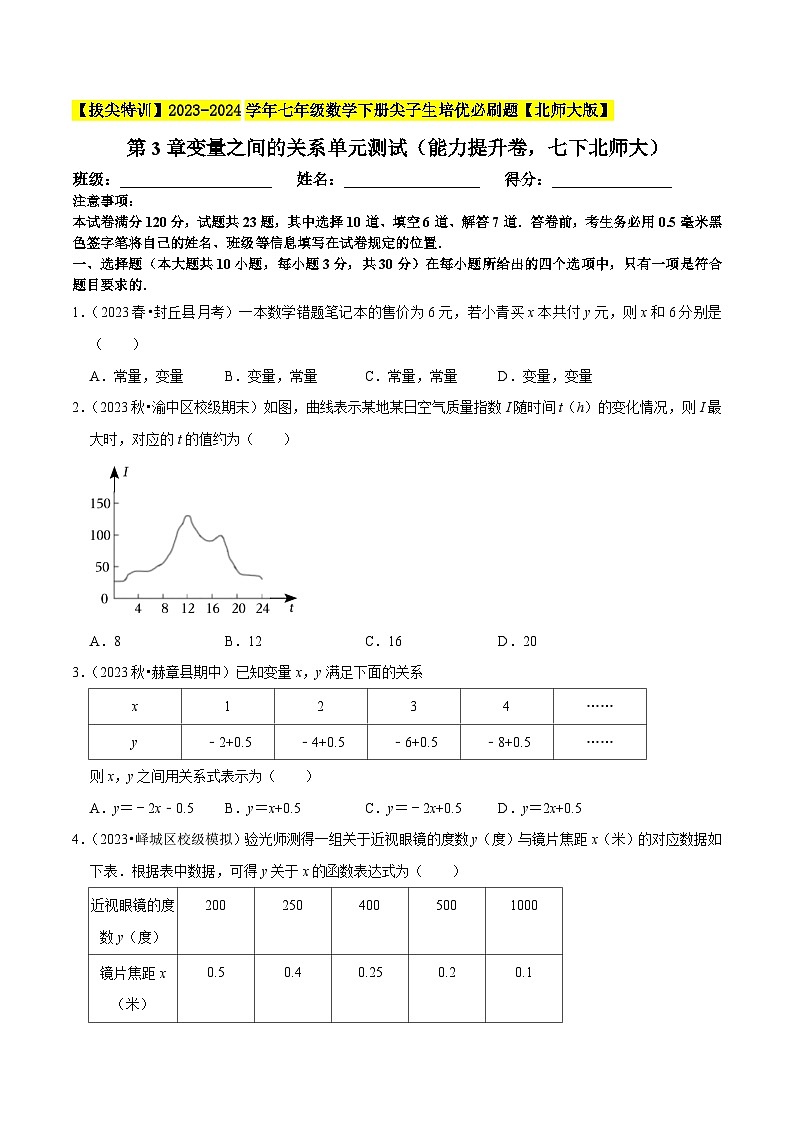
2．（2023秋•渝中区校级期末）如图，曲线表示某地某日空气质量指数I随时间t（h）的变化情况，则I最大时，对应的t的值约为（ ）
A．8B．12C．16D．20
3．（2023秋•赫章县期中）已知变量x，y满足下面的关系
则x，y之间用关系式表示为（ ）
A．y＝﹣2x﹣0.5B．y＝x+0.5C．y＝﹣2x+0.5D．y＝2x+0.5
4．（2023•峄城区校级模拟）验光师测得一组关于近视眼镜的度数y（度）与镜片焦距x（米）的对应数据如下表．根据表中数据，可得y关于x的函数表达式为（ ）
A．y＝B．y＝C．y＝D．y＝
5．（2023•南京模拟）如图，把两根木条AB和AC的一端A用螺栓固定在一起，木条AC自由转动至AC′位置．在转动过程中，下面的量是常量的为（ ）
A．∠BAC的度数B．BC的长度
C．△ABCC的面积D．AC的长度
6．（2023春•西昌市校级月考）从西昌到成都大约有560千米，某天小丽一家准备自驾车从西昌到成都参观动物园，在这个过程中，如果设行驶速度为v千米/小时，行驶的时间为t小时，其中变量是（ ）
A．560、tB．t、vC．560、vD．560、v、t
7．（2023•隆昌市校级三模）物理课上，老师用弹簧秤将铁块悬于盛有水的水槽中，然后匀速向上提起，直到铁块完全露出水面一定高度，则能反映弹簧秤的读数y与铁块被提起的高度x之间的函数关系的大致图象是（ ）
A．B．
C．D．
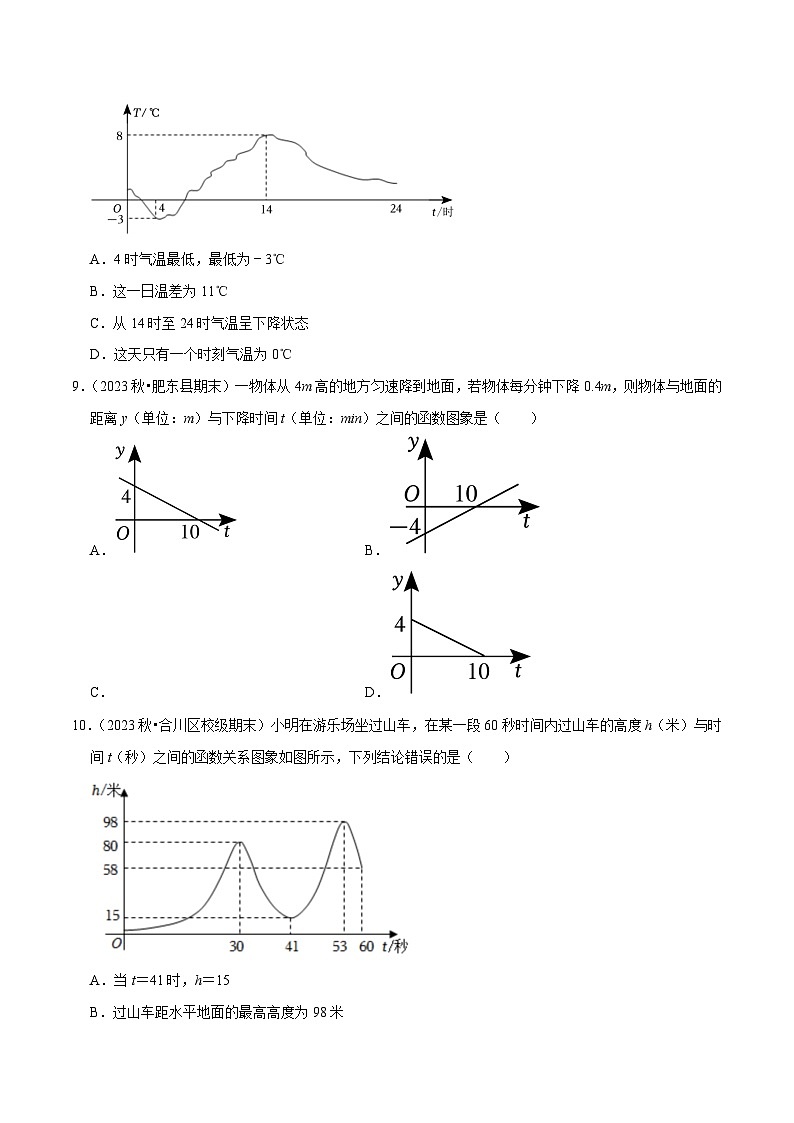
8．（2023•凤泉区校级一模）如图是某地一日气温T随时间t的变化图象．下列说法中错误的是（ ）
A．4时气温最低，最低为﹣3℃
B．这一日温差为11℃
C．从14时至24时气温呈下降状态
D．这天只有一个时刻气温为0℃
9．（2023秋•肥东县期末）一物体从4m高的地方匀速降到地面，若物体每分钟下降0.4m，则物体与地面的距离y（单位：m）与下降时间t（单位：min）之间的函数图象是（ ）
A．B．
C．D．
10．（2023秋•合川区校级期末）小明在游乐场坐过山车，在某一段60秒时间内过山车的高度h（米）与时间t（秒）之间的函数关系图象如图所示，下列结论错误的是（ ）
A．当t＝41时，h＝15
B．过山车距水平地面的最高高度为98米
C．在0≤t≤60范围内，当过山车高度是80米时，t的值只能等于30
D．当41＜t≤53时，高度h（米）随时间t（秒）的增大而增大
二、填空题（本大题共6小题，每小题4分，共24分）请把答案直接填写在横线上
11．（2023秋•东昌府区期末）汽车开始行驶时油箱内有油40升，如果每小时耗油5升，则油箱内余油量Q（升）与行驶时间t（小时）的关系是 ，其中的常量是 ，变量是 ．
12．（2023秋•杨浦区期末）如图：某人从甲地行走到乙地的路程S（千米）与时间t（小时）的函数关系如图所示，那么此人行走5千米，所用的时间是 小时．
13．（2023春•晋江市校级月考）某水库的水位在某段时间内持续上涨，初始的水位高度为6米，水位以每小时0.3米的速度匀速上升，则水库的水位高度y米与时间x小时的函数关系式为 ．
14．（2023•滨海县校级开学）根据下面的研究弹簧长度与所挂物体重量关系的实验表格，当所挂物体重量为3.5kg时，弹簧比原来伸长 cm．
15．（2023秋•城阳区期末）如图，为一个沙漏在计时过程中所剩沙子质量y（克）与时间x（小时）之间关系的图象，则从开始计时到沙子漏光所需的时间为 小时．
16．（2023秋•黑山县期中）观察下列各正方形图案，每条边上有n（n＞2）个圆点，每个图案中圆点的总数是S．按此规律推断出S与n的关系式为 ．
三、解答题（本大题共7小题，共66分．解答时应写出文字说明、证明过程或演算步骤）
17．（2023秋•聊城期末）某超市销售某种商品时，其销售数量x（kg）与售价y（元）的对应关系如表所示：
请你根据表中所提供的信息列出y与x之间的关系式，指出其中的常量与变量，并求出当销售数量为2.5kg时的售价．
18．（2023秋•靖西市期中）如图是某地区一天的气温随时间变化的图象：
（1）气温在哪段时间是上升的？
（2）最高气温和最低气温分别是多少摄氏度？
19．（2023秋•平阴县期中）小敏上午8：00从家里出发，骑车去一家超市购物，然后从这家超市返回家中，小敏离家的路程y（米）和所经过的时间x（分）之间的函数图象如图所示．请根据图象回答下列问题：
（1）小敏在超市逗留了 分钟；
（2）小敏去超市途中的速度是多少？
（3）小敏几点几分返回到家？
20．（2023秋•深圳期中）将长为38cm，宽为5cm的长方形白纸按如图所示的方法黏合在一起，黏合部分的白纸宽为2cm．
（1）求5张白纸黏合的长度；
（2）设x张白纸黏合后的总长为ycm，写出y与x的函数关系式．
21．（2023春•新城区校级期中）春节前，某面粉加工厂接到加工任务，要求5天内加工完220吨面粉，加工厂安排甲、乙两组共同完成加工任务．乙组加工中途停工一段时间维修设备，然后提高加工效率继续加工，直到与甲队同时完成加工任务为止．设甲、乙两组各自加工面粉数量y（吨）与甲组加工时间x（天）之间的关系如图所示，结合图象，解答下列问题：
（1）乙组中途休息了几天；甲组每天加工面粉多少吨？
（2）乙组提高加工效率后，每天加工面粉多少吨？
（3）加工几天，甲、乙两组共完成总任务的一半？
22．（2023春•胶州市期中）如图，某种型号的自行车每节链条的长度为2.5cm，交叉重叠部分的圆的直径为0.8cm．
（1）观察图形并补全下表：
（2）如果n节链条的总长度是ycm，写出y与n之间的关系式．
23．（2023春•满洲里市校级期末）小红星期天从家里出发骑车去舅舅家做客，当她骑了一段路时，想起要买个礼物送给表弟，于是又折回到刚经过的一家商店，买好礼物后又继续骑车去舅舅家，以下是她本次去舅舅家所用的时间与路程的关系式示意图．根据图中提供的信息回答下列问题：
（1）小红家到舅舅家的路程是 米，小红在商店停留了 分钟；
（2）在整个去舅舅家的途中时间段小红骑车速度最快，最快的速度 米/分．
（3）本次去舅舅家的行程中，小红一共行驶了多少米？一共用了多少分钟？
x
1
2
3
4
……
y
﹣2+0.5
﹣4+0.5
﹣6+0.5
﹣8+0.5
……
近视眼镜的度数y（度）
200
250
400
500
1000
镜片焦距x（米）
0.5
0.4
0.25
0.2
0.1
所挂物体重量x（kg）
1
3
4
5
弹簧长度y（cm）
10
14
16
18
销售数量x（kg）
1
2
3
4
5
…
售价y（元）
8+0.4
16+0.8
24+1.2
32+1.6
40+2.0
…
链条节数/节
3
4
6
链条长度/cm



【拔尖特训】2023-2024学年七年级数学下册尖子生培优必刷题【北师大版】
第3章变量之间的关系单元测试（能力提升卷，七下北师大）
班级：___________________ 姓名：_________________ 得分：_______________
注意事项：
本试卷满分120分，试题共23题，其中选择10道、填空6道、解答7道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2023春•封丘县月考）一本数学错题笔记本的售价为6元，若小青买x本共付y元，则x和6分别是（ ）
A．常量，变量B．变量，常量C．常量，常量D．变量，变量
分析：根据变量、常量的定义，结合具体的问题情况进行判断即可．
解析：解：小青购买错题本的本数x是变化的，因此x是变量，而单价为每本6元，是不变的量，因此6是常量，
故选：B．
2．（2023秋•渝中区校级期末）如图，曲线表示某地某日空气质量指数I随时间t（h）的变化情况，则I最大时，对应的t的值约为（ ）
A．8B．12C．16D．20
分析：结合图象可得I最大时，对应的t的值约为12．
解析：解：根据图象可以看出I最大时，对应的t的值约为12．
故选：B．
3．（2023秋•赫章县期中）已知变量x，y满足下面的关系
则x，y之间用关系式表示为（ ）
A．y＝﹣2x﹣0.5B．y＝x+0.5C．y＝﹣2x+0.5D．y＝2x+0.5
分析：观察这几组数据，找到其中的规律，然后再答案中找出符合要求的关系式．
解析：解：观察图表可知，每对x，y的对应值，y是x的﹣2倍加0.5，
故y与x之间的函数关系式：y＝﹣2x+0.5．
故选：C．
4．（2023•峄城区校级模拟）验光师测得一组关于近视眼镜的度数y（度）与镜片焦距x（米）的对应数据如下表．根据表中数据，可得y关于x的函数表达式为（ ）
A．y＝B．y＝C．y＝D．y＝
分析：直接利用已知数据可得xy＝100，进而得出答案．
解析：解：由表格中数据可得：xy＝100，
故y关于x的函数表达式为：y＝．
故选：A．
5．（2023•南京模拟）如图，把两根木条AB和AC的一端A用螺栓固定在一起，木条AC自由转动至AC′位置．在转动过程中，下面的量是常量的为（ ）
A．∠BAC的度数B．BC的长度
C．△ABCC的面积D．AC的长度
分析：根据常量和变量的定义进行判断．
解析：解：木条AC自由转动至AC′位置中，
AC的长度始终保持不变，
∴AC的长度是常量．
故选：D．
6．（2023春•西昌市校级月考）从西昌到成都大约有560千米，某天小丽一家准备自驾车从西昌到成都参观动物园，在这个过程中，如果设行驶速度为v千米/小时，行驶的时间为t小时，其中变量是（ ）
A．560、tB．t、vC．560、vD．560、v、t
分析：根据常量与变量的定义：在一个变化的过程中，数值发生变化的量称为变量；数值始终不变的量称为常量解答即可．
解析：解：从西昌到成都大约有560千米，在这个过程中，行驶速度为v千米/小时，行驶的时间为t小时，其中是变量的是t，v．
故选：B．
7．（2023•隆昌市校级三模）物理课上，老师用弹簧秤将铁块悬于盛有水的水槽中，然后匀速向上提起，直到铁块完全露出水面一定高度，则能反映弹簧秤的读数y与铁块被提起的高度x之间的函数关系的大致图象是（ ）
A．B．
C．D．
分析：根据在铁块开始露出水面到完全露出水面时，排开水的体积逐渐变小，根据阿基米德原理和称重法可知y的变化，注意铁块露出水面前读数y不变，离开水面后y不变，即可得出答案．
解析：解：露出水面前排开水的体积不变，受到的浮力不变，根据称重法可知y不变；
铁块开始露出水面到完全露出水面时，排开水的体积逐渐变小，根据阿基米德原理可知受到的浮力变小，根据称重法可知y变大；
铁块完全露出水面后一定高度，不再受浮力的作用，弹簧秤的读数为铁块的重力，故y不变．
故选：C．
8．（2023•凤泉区校级一模）如图是某地一日气温T随时间t的变化图象．下列说法中错误的是（ ）
A．4时气温最低，最低为﹣3℃
B．这一日温差为11℃
C．从14时至24时气温呈下降状态
D．这天只有一个时刻气温为0℃
分析：分析变化趋势和具体数值，即可求出答案．
解析：解：A．由函数图象知，4时气温达到最低，原说法正确，不符合题意；
B．这一日温差为：8﹣（﹣3）＝11（℃），原说法正确，不符合题意；
C．从14时至24时气温整体呈现下降状态，原说法正确，不符合题意；
D．这天有两个时刻气温为0℃，原说法错误，符合题意．
故选：D．
9．（2023秋•肥东县期末）一物体从4m高的地方匀速降到地面，若物体每分钟下降0.4m，则物体与地面的距离y（单位：m）与下降时间t（单位：min）之间的函数图象是（ ）
A．B．
C．D．
分析：根据题意可确定关系式为：y＝4﹣0.4t，从而可以解答本题．
解析：解：由题意得：y＝4﹣0.4t，
当y＝0时，4﹣0.4t＝0，t＝10．
故选：D．
10．（2023秋•合川区校级期末）小明在游乐场坐过山车，在某一段60秒时间内过山车的高度h（米）与时间t（秒）之间的函数关系图象如图所示，下列结论错误的是（ ）
A．当t＝41时，h＝15
B．过山车距水平地面的最高高度为98米
C．在0≤t≤60范围内，当过山车高度是80米时，t的值只能等于30
D．当41＜t≤53时，高度h（米）随时间t（秒）的增大而增大
分析：A选项根据某一分钟内过山车高度h（米）与时间t（秒）之间的函数图象，即可得出当t＝41秒时，h的值；B选项根据图象判断即可；C选项结合图象可得在这1分钟内，有4个时间点，过山车高度是80米；D选项通过函数图象的增减性判断即可．
解析：解：A．由图象可知，当t＝41秒时，h的值是15米，故本选项不合题意；
B．由图象可知，过山车距水平地面的最高高度为98米，故本选项不合题意；
C．由图象可知，在0≤t≤60范围内，当过山车高度是80米时，t的值有3个，原说法错误，故本选项符合题意；
D．由图象可知，当41＜r≤53时，高度h（米）随时间t（秒）的增大而增大；故本选项不合题意；
故选：C．
二．填空题（共6小题）
11．（2023秋•东昌府区期末）汽车开始行驶时油箱内有油40升，如果每小时耗油5升，则油箱内余油量Q（升）与行驶时间t（小时）的关系是 Q＝40﹣5t ，其中的常量是 40、﹣5 ，变量是 Q、t ．
分析：根据油箱内剩余油量＝油箱内总油量﹣消耗掉的油，进而得出关系式，再利用常量、变量的定义得出答案．
解析：解：根据题意可得：
油箱内剩余油量Q（升）与行驶时间t（小时）的函数关系为：Q＝40﹣5t，
常量为：40、﹣5，
变量为：Q、t．
故答案为：Q＝40﹣5t；40、﹣5；Q、t．
12．（2023秋•杨浦区期末）如图：某人从甲地行走到乙地的路程S（千米）与时间t（小时）的函数关系如图所示，那么此人行走5千米，所用的时间是 1.25 小时．
分析：根据速度＝路程÷时间求出行驶的速度，再根据时间＝路程÷速度进行计算即可得解．
解析：解：由图可知，速度＝12÷3＝4千米/时，
所以，行走5千米所用的时间＝5÷4＝1.25小时．
故答案为：1.25．
13．（2023春•晋江市校级月考）某水库的水位在某段时间内持续上涨，初始的水位高度为6米，水位以每小时0.3米的速度匀速上升，则水库的水位高度y米与时间x小时的函数关系式为 y＝6+0.3x ．
分析：根据高度等于速度乘以时间列出关系式解答即可．
解析：解：因为初始的水位高度为6米，水位以每小时0.3米的速度匀速上升，
所以k＝0.3，b＝6，
根据题意可得：y＝6+0.3x，
故答案为：y＝6+0.3x．
14．（2023•滨海县校级开学）根据下面的研究弹簧长度与所挂物体重量关系的实验表格，当所挂物体重量为3.5kg时，弹簧比原来伸长 7 cm．
分析：估计y与x的之间的关系是一次函数关系，用待定系数法求出函数关系式，再验证表格中其它各组数据是否满足求出的关系式，若都满足就确定是一次函数关系，确定关系式，再依据关系式求出x＝3.5时y﹣8的值即可．
解析：解：设y与x之间的关系可能是一次函数关系，设关系式为y＝kx+b，
把（1，10），（3，14）代入得：
，解得：k＝2，b＝8，
∴y与x之间的关系式为y＝2x+8，
经验证：（4，16），（5，18）也满足上述关系，
因此y与x的函数关系式就是y＝2x+8，
当x＝0时，y＝8，即不挂物体时弹簧的原长为8cm．
当x＝3.5时，y＝2×3.5+8＝15，
15﹣8＝7cm，
故答案为：7．
15．（2023秋•城阳区期末）如图，为一个沙漏在计时过程中所剩沙子质量y（克）与时间x（小时）之间关系的图象，则从开始计时到沙子漏光所需的时间为 小时．
分析：根据图象可得沙漏漏沙的速度，从而得出从开始计时到沙子漏光所需的时间．
解析：解：沙漏漏沙的速度为：＝（克/小时），
∴从开始计时到沙子漏光所需的时间为：15÷＝（小时）．
故答案为：．
16．（2023秋•黑山县期中）观察下列各正方形图案，每条边上有n（n＞2）个圆点，每个图案中圆点的总数是S．按此规律推断出S与n的关系式为 4n﹣4 ．
分析：注意观察前三个图形中圆点的个数可以发现分别为：4，8，12，后一个图形中的圆点个数比前一个图形中圆点多4，所以可得S与n的关系式为：S＝4n﹣4．
解析：解：n＝2时，S＝4；
n＝3时，S＝4+1×4＝8；
n＝4时，S＝4+2×4＝12，
∴S＝4+（n﹣2）×4
＝4n﹣4
＝4（n﹣1）．
三．解答题（共8小题）
17．（2023秋•聊城期末）某超市销售某种商品时，其销售数量x（kg）与售价y（元）的对应关系如表所示：
请你根据表中所提供的信息列出y与x之间的关系式，指出其中的常量与变量，并求出当销售数量为2.5kg时的售价．
分析：先根据数量x与售价y表中所示所提供的信息，列出售价y与数量x的函数关系式y＝（8+0.4）x，再将x的值为2.5千克代入上式中即可求出售价．
解析：解：y＝（8+0.4）x＝8.4x，其中常量为8.4，变量为x、y，
当x＝2.5千克时，
y＝8.4×2.5＝21（元）．
所以当销售数量为2.5千克时，售价是21元．
18．（2023秋•靖西市期中）如图是某地区一天的气温随时间变化的图象：
（1）气温在哪段时间是上升的？
（2）最高气温和最低气温分别是多少摄氏度？
分析：（1）直接根据图象信息回答即可；
（2）直接根据图象信息回答即可．
解析：解：（1）由图象可知，气温在4到14时上升；
（2）由图象可知，最高气温是8℃，最低气温是﹣2℃．
19．（2023秋•平阴县期中）小敏上午8：00从家里出发，骑车去一家超市购物，然后从这家超市返回家中，小敏离家的路程y（米）和所经过的时间x（分）之间的函数图象如图所示．请根据图象回答下列问题：
（1）小敏在超市逗留了 30 分钟；
（2）小敏去超市途中的速度是多少？
（3）小敏几点几分返回到家？
分析：（1）由图象得小敏在超市逗留时间可列式为40﹣10，再进行求解；
（2）先求得小敏返回时的速度，再求得小敏返回时的时间，即可求得此题结果．
解析：解：（1）40﹣10＝30（分钟），
∴小敏在超市逗留了30分钟，
故答案为：30；
（2）3000÷10＝300（米/分钟），
答：小敏去超市途中的速度是300米/分钟；
（3）3000÷
＝3000÷200
＝15（分钟），
40+15＝55（分），
∴小敏8点55分返回到家，
答：小敏8点55分返回到家．
20．（2023秋•深圳期中）将长为38cm，宽为5cm的长方形白纸按如图所示的方法黏合在一起，黏合部分的白纸宽为2cm．
（1）求5张白纸黏合的长度；
（2）设x张白纸黏合后的总长为ycm，写出y与x的函数关系式．
分析：（1）根据粘连的规律可得答案，即5张的总长度，减去4个重叠部分的宽度即可；
（2）根据粘连的规律可得x张白纸黏合后的总长y，即x张白纸的总长度，减去（x﹣1）个重合部分的宽度即可．
解析：解：（1）5张白纸黏合的长度为38×5﹣2×（5﹣1）＝182（cm），
答：5张白纸黏合的长度为182cm；
（2）y＝38x﹣2（x﹣1）＝36x+2，
答：y与x的函数关系式为y＝36x+2．
21．（2023春•新城区校级期中）春节前，某面粉加工厂接到加工任务，要求5天内加工完220吨面粉，加工厂安排甲、乙两组共同完成加工任务．乙组加工中途停工一段时间维修设备，然后提高加工效率继续加工，直到与甲队同时完成加工任务为止．设甲、乙两组各自加工面粉数量y（吨）与甲组加工时间x（天）之间的关系如图所示，结合图象，解答下列问题：
（1）乙组中途休息了几天；甲组每天加工面粉多少吨？
（2）乙组提高加工效率后，每天加工面粉多少吨？
（3）加工几天，甲、乙两组共完成总任务的一半？
分析：（1）根据图象的横纵坐标表示的意义，进行计算即可得出答案；
（2）根据“工作效率＝工作总量÷工作时间”可得答案；
（3）根据题意列式解答即可．
解析：解：（1）由图象可得：2﹣1＝1（天），即乙组加工中途停工1天，
甲组每天加工面粉数量为：＝20（吨）；
（2）＝35（吨），
答：乙组提高加工效率后，每天加工面粉35吨；
（3）结合图象可知，加工3天后面粉数量为：60+15+35＝110（吨），完成总任务的一半．
22．（2023春•胶州市期中）如图，某种型号的自行车每节链条的长度为2.5cm，交叉重叠部分的圆的直径为0.8cm．
（1）观察图形并补全下表：
（2）如果n节链条的总长度是ycm，写出y与n之间的关系式．
分析：（1）根据图形找出规律计算4节链条的长度即可；
（2）由（1）写出表示链条节数的一般式．
解析：解：（1）根据图形可得出：
3节链条的长度为：2.5×3﹣0.8×2＝5.9，
4节链条的长度为：2.5×4﹣0.8×3＝7.6，
6节链条的长度为：2.5×6﹣0.8×5＝11．
故答案为：5.9；7.6；11；
（2）由（1）可得n节链条长为：y＝2.5n﹣0.8（n﹣1）＝1.7n+0.8，
∴y与n之间的关系式为：y＝1.7n+0.8．
23．（2023春•满洲里市校级期末）小红星期天从家里出发骑车去舅舅家做客，当她骑了一段路时，想起要买个礼物送给表弟，于是又折回到刚经过的一家商店，买好礼物后又继续骑车去舅舅家，以下是她本次去舅舅家所用的时间与路程的关系式示意图．根据图中提供的信息回答下列问题：
（1）小红家到舅舅家的路程是 1500 米，小红在商店停留了 4 分钟；
（2）在整个去舅舅家的途中时间段小红骑车速度最快，最快的速度 450 米/分．
（3）本次去舅舅家的行程中，小红一共行驶了多少米？一共用了多少分钟？
分析：（1）根据图象，路程的最大值即为小红家到舅舅家的路程；读图，对应题意找到其在商店停留的时间段，进而可得其在商店停留的时间；
（2）分析图象，找函数变化最快的一段，可得小红骑车速度最快的时间段，进而可得其速度；
（3）分开始行驶的路程，折回商店行驶的路程以及从商店到舅舅家行驶的路程三段相加即可求得小红一共行驶路程；读图即可求得本次去舅舅家的行程中，小红一共用的时间．
解析：解：（1）根据图象舅舅家纵坐标为1500，小红家的纵坐标为0，
故小红家到舅舅家的路程是1500米；
根据题意，小红在商店停留的时间为从8分到12分，
故小红在商店停留了4分钟．
故答案为：1500，4；
（2）根据图象，12≤x≤14时，直线最陡，
故小红在12﹣14分钟最快，速度为＝450（米/分）．
故答案为：450；
（3）读图可得：小红共行驶了1200+600+900＝2700米，共用了14分钟．
答：小红共行驶了2700米，共用了14分钟．
x
1
2
3
4
……
y
﹣2+0.5
﹣4+0.5
﹣6+0.5
﹣8+0.5
……
近视眼镜的度数y（度）
200
250
400
500
1000
镜片焦距x（米）
0.5
0.4
0.25
0.2
0.1
所挂物体重量x（kg）
1
3
4
5
弹簧长度y（cm）
10
14
16
18
销售数量x（kg）
1
2
3
4
5
…
售价y（元）
8+0.4
16+0.8
24+1.2
32+1.6
40+2.0
…
链条节数/节
3
4
6
链条长度/cm
5.9
7.6
11