



福建省厦门市松柏中学2023-2024学年七年级下学期期中数学试题(原卷版+解析版)
展开1. 在下列所给出坐标的点中,在第二象限的是
A. (2,3)B. (﹣2,3)C. (﹣2,﹣3)D. (2,﹣3)
【答案】B
【解析】
【详解】解:∵第二象限内点的横坐标是负数,纵坐标是正数,
∴(2,3)、(-2,3)、(-2,-3)、(2,-3)中只有(-2,3)在第二象限.
故选:B.
2. 9 的算术平方根是( )
A. 3B. -3C. ±3D. 81
【答案】A
【解析】
【分析】根据算术平方根的性质计算即可;
【详解】9的算术平方根是3.
故答案选A.
【点睛】本题主要考查了算术平方根的计算,准确计算是解题的关键.
3. 在实数,0,,3.1415926,,0.21,,(相邻两个5之间的3依次增加1个)中,无理数的个数为( )
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
【分析】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:,等;开方开不尽的数;以及像(每两个1之间的0增加一个)等有这样规律的数.无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【详解】解:,
在实数,0,,3.1415926,,0.21,,(相邻两个5之间3依次增加1个)中,无理数有,,(相邻两个5之间的3依次增加1个),共3个.
故选:C
4. 如图,已知,,平分,则的度数为( )
A. B. C. D.
【答案】B
【解析】
【点睛】利用两直线平行内错角相等和角平分线的性质求得所求角的度数.
【详解】∵,∴,
∵平分,∴,
故选B.
【分析】本题考查内错角和角平分线性质,掌握这些是本题关键.
5. 若方程ax+3y=2+4x是关于的二元一次方程,则a满足( )
A. a≠1B. a≠2C. a≠3D. a≠4
【答案】D
【解析】
【分析】移项整理给出的方程,根据二元一次方程的定义确定a的范围.
【详解】解:移项,得ax−4x+3y−2=0,
整理,得(a−4)x+3y−2=0.
∵方程是关于x、y的二元一次方程,
∴a−4≠0.
∴a≠4.
故选:D.
【点睛】本题考查了二元一次方程的定义,理解二元一次方程的定义是解决本题的关键.二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程.
6. 若,,则下列不等式不一定成立的是( )
A B. C. D.
【答案】D
【解析】
【分析】根据不等式的性质,逐项判断即可求解.
【详解】解:A、若,,则,故本选项正确,不符合题意;
B、若,,则,故本选项正确,不符合题意;
C、若,则 ,若,则,故本选项正确,不符合题意;
D、若,,当 时,,故本选项错误,符合题意;
故选:D
【点睛】本题主要考查了不等式的性质,熟练掌握不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.
7. 下列画出的直线a与b不一定平行的是( )
A. B.
C. D.
【答案】A
【解析】
【分析】根据平行线的判定定理即可解答.
【详解】解:A.直线a与b不一定平行,故本选项符合题意;
B.根据同旁内角互补,两直线平行可得a∥b,故本选项不符合题意;
C.根据同位角相等,两直线平行可得a∥b,故本选项不符合题意;
D.根据同位角相等,两直线平行可得a∥b,故本选项不符合题意;
故选:A.
【点睛】本题考查了平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
8. 明代《算法统宗》有一首饮酒数学诗:“醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多醇酒几多醇?”这首诗是说:“好酒一瓶,可以醉倒3位客人;薄酒三瓶,可以醉倒1位客人,如今33位客人醉倒了,他们总共饮19瓶酒.试问:其中好酒、薄酒分别是多少瓶?”设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为( )
A. B. C. D.
【答案】A
【解析】
【分析】根据题意,列方程求解即可.
【详解】解:设有好酒x瓶,薄酒y瓶,
根据“总共饮19瓶酒”可得:
根据“好酒一瓶,可以醉倒3位客人;薄酒三瓶,可以醉倒1位客人,如今33位客人醉倒了”,可得:
综上:,
故选:A
【点睛】此题考查了列二元一次方程组,解题的关键是理解题意,正确列出二元一次方程组.
9. 下列命题:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③4是的立方根;④带根号的数都是无理数;⑤所有实数都可以用数轴上的点表示,反过来,数轴上的所有点都表示实数,真命题的个数有( )
A. 0个B. 1个C. 2个D. 3个
【答案】B
【解析】
【分析】根据平行公理,立方根的定义,无理数的定义,实数的性质,进行判断,即可.
【详解】经过直线外一点有且只有一条直线与已知直线平行,
∴错误;
在同一平面内过一点有且只有一条直线与已知直线垂直,
∴错误;
是的立方根,
∴错误;
带根号的不一定是无理数,如是有理数,
∴错误;
∵实数与数轴上的点是一一对应的关系,
∴正确;
故选:B.
【点睛】本题考查命题、定理与证明,解题的关键是掌握平行公理,立方根的定义,无理数的定义,实数的性质.
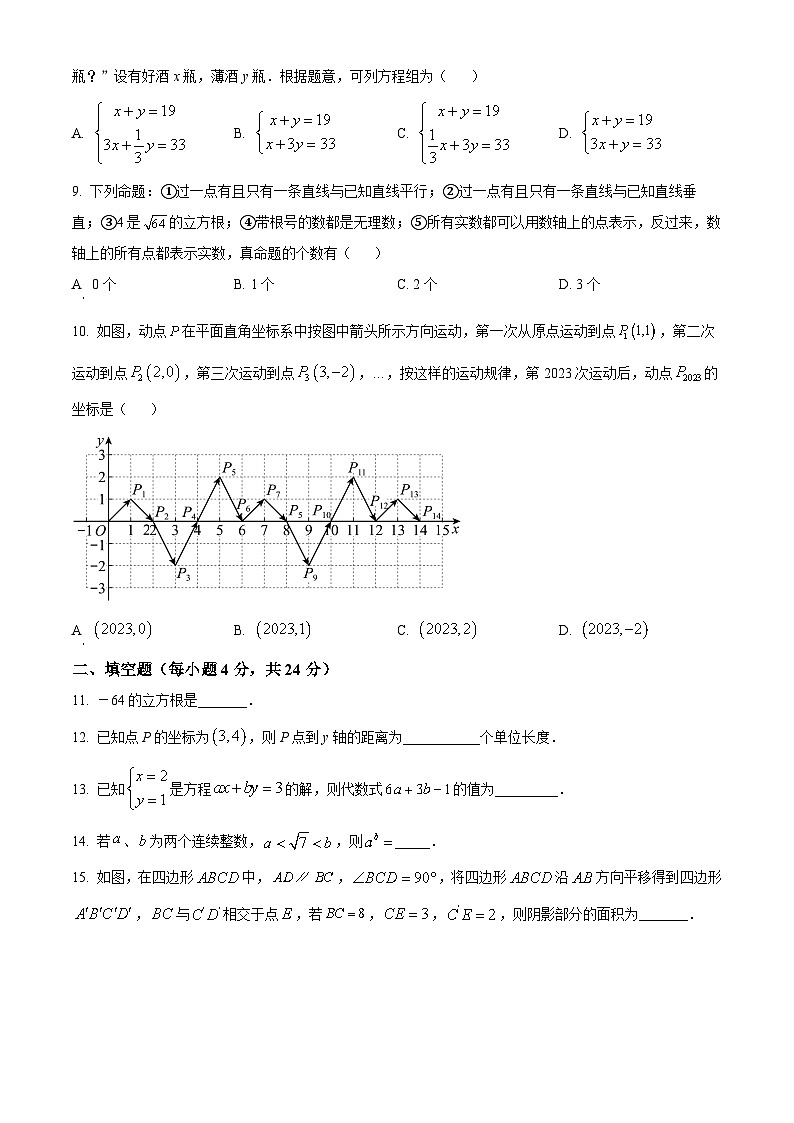
10. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第一次从原点运动到点,第二次运动到点,第三次运动到点,…,按这样的运动规律,第2023次运动后,动点的坐标是( )
A. B. C. D.
【答案】B
【解析】
【分析】观察图象,得出点P运动的规律,再根据循环规律可得答案.
【详解】解:∵动点P第一次从原点O运动到点,第二次运动到点,第三次运动到,第四次运动到,第五次运动到,第六次运动到,…,
∴横坐标与下标相同,纵坐标每6次运动组成一个循环:1,0,,0,2,0;
∵,
∴经过第2023次运动后,动点P的横坐标为2023,纵坐标是1,即:.
故选:B.
【点睛】本题考查了规律型点的坐标,数形结合并从图象中发现循环规律:纵坐标每6次运动组成一个循环是解题的关键.
二、填空题(每小题4分,共24分)
11. -64的立方根是_______.
【答案】-4
【解析】
【分析】直接利用立方根的意义,一个数的立方等于a,则a的立方根是这个数进行求解.
【详解】解:根据立方根的意义,一个数的立方等于a,则a的立方根是这个数,
可知-64立方根为-4.
故答案为:-4.
【点睛】本题考查了立方根,解题的关键是掌握一个数的立方等于a,则a的立方根是这个数.
12. 已知点P的坐标为,则P点到y轴的距离为___________个单位长度.
【答案】3
【解析】
【分析】直接利用点的坐标特点,横坐标绝对值就是到轴距离,即可得出答案.
【详解】解:点到轴的距离是:.
即点到轴的距离为3个单位长度.
故答案为:3.
【点睛】此题主要考查了点的坐标,正确掌握点的坐标特点是解题关键.
13. 已知是方程的解,则代数式的值为_________.
【答案】
【解析】
【分析】根据二元一次方程的解的定义,得出,整体代入代数式求值即可求解.
【详解】解:∵是方程的解,
∴,
∴
,
故答案为:.
【点睛】本题考查了二元一次方程的解的定义,代数式求值,熟练掌握以上知识是解题的关键.使得方程左右两边相等的未知数的值是方程的解.
14. 若、为两个连续整数,,则_____.
【答案】8
【解析】
【分析】本题考查了估算无理数的大小,能估算出的范围是解此题的关键.
【详解】解:、为两个连续整数,,,
,,
,
故答案为:8.
15. 如图,在四边形中,,,将四边形沿方向平移得到四边形,与相交于点,若,,,则阴影部分的面积为_______.
【答案】13
【解析】
【分析】本题考查了平移的性质,熟练掌握平移的性质是解题的关键.根据平移的性质得出四边形的面积与四边形的面积相等,,,,从而得到阴影部分的面积等于梯形的面积,根据梯形面积公式求出梯形的面积即可.
【详解】解:由平移的性质得:
四边形的面积与四边形的面积相等,,,,
阴影部分的面积为四边形的面积减去四边形的面积,
四边形的面积为四边形的面积减去四边形的面积,
阴影部分的面积等于四边形的面积,
,,
四边形的面积为:,
故答案:13.
16. 将一副三角板按如图放置,小明得到下列结论:①如果∠2=30°,则有AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则有∠2=30°;④如果∠CAD=150°,则∠4=∠C;那么其中正确的结论有________
【答案】①②④
【解析】
【分析】根据平行线的判定定理判断①;根据角的关系判断②即可;根据平行线的性质定理判断③;根据①的结论和平行线的性质定理判断④.
【详解】∵∠2=30°,
∴∠1=60°,
又∵∠E=60°,
∴∠1=∠E,
∴AC//DE,故①正确;
∵∠1+∠2=90°,∠2+∠3=90°,
即∠BAE+∠CAD=∠1+∠2+∠2+∠3=90°+90°=180°,故②正确;
∵BC//AD,
∴∠1+∠2+∠3+∠C=180°,
又∵∠C=45°,∠1+∠2=90°,
∴∠3=45°,
∴∠2=90°−45°=45°,故③错误;
∵∠D=30°,∠CAD=150°,
∴∠CAD+∠D=180°,
∴AC//DE,
∴∠4=∠C,故④正确.
故答案为①②④
【点睛】此题考查平行线的判定定理和性质,角的关系,解题关键在于利用判定定理进行判断
三、解答题(共86分)
17. 计算:
(1);
(2).
【答案】(1)
(2)
【解析】
【分析】本题考查实数的运算,掌握算术平方根、立方根以及实数的运算方法是正确解答的前提.
(1)先计算乘方,立方根、算术平方根,再计算乘法,最后计算加减即可;
(2)根据算术平方根,绝对值的定义进行计算即可.
【小问1详解】
解:原式
;
【小问2详解】
解:原式
.
18. 求下列各式的值;
(1);
(2)
【答案】(1),
(2)
【解析】
【分析】(1)先移项,然后再根据平方根定义,解方程即可;
(2)根据立方根定义,解方程即可.
【小问1详解】
解:,
移项得:,
开平方得:,
解得:,;
【小问2详解】
解:,
方程两边同除以8得:,
开立方得:,
解得:.
【点睛】本题主要考查了利用平方根和立方根解方程,解题的关键是熟练掌握平方根和立方根定义.
19. 如图,平面直角坐标系中,的顶点都在网格点上,其中,C点坐标为.
(1)写出点A、B的坐标:A( , )、B( , )
(2)将平移后得到,点A的对应点为,画出,并写出点B、点C的对应点的坐标:( , )、( , )
(3)的面积是 .
【答案】(1)2;﹣1;4;3.
(2)图见解析;2;4;﹣1;3.
(3)5
【解析】
【分析】本题主要考查了坐标与图形变化—平移,坐标与图形:
(1)根据点的位置即可得;
(2)先根据点的坐标可得平移方式,再根据平移的性质,作图即可;
(3)结合图形,利用一个大长方形的面积减去三个小直角三角形的面积即可得.
小问1详解】
解:由平面直角坐标系可知,点的坐标为,点的坐标为,
故答案为:;.
【小问2详解】
解:点对应点的坐标为,
将点A先向左平移2个单位,再向上平移1个单位即可得到点,
,
,即,
则画出如下所示:
故答案为:2;4;;
【小问3详解】
解:的面积为,
故答案为:5.
20. 陈老师为学校购买运动会的奖品后,回学校向后勤处王老师交账说:“我买了两种书,共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”王老师算了一下,说:“你肯定弄错了.”王老师为什么说他弄错了?试用方程的知识给予解释.
【答案】见解析
【解析】
【分析】本题主要考查了一元一次方程的实际应用,设单价为8元的课外书为x本,则单价为12元的课外书为本,根据总费用为元列出方程求解即可.
【详解】解:设单价为8元的课外书为x本,
由题意得,
解得:(不符合题意).
∵在此题中x是正整数,
∴王老师说他肯定搞错了.
21. 请你补全证明过程或推理依据:
已知:如图,四边形,点、分别在边两方的延长线上,连接,若,.求证:.
证明:点在的延长线上(已知)
又 (已知)
又(已知)
【答案】1;平角定义;1;同角的补角相等;3;等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
【解析】
【分析】本题主要考查平行线的性质与判定以及同角的补角的相等,熟练掌握平行线的性质与判定是解题关键.证明转化为证明.欲证,可证.由题知,转化为证明.欲证,可证.根据,,则可证.
【详解】证明:点在的延长线上(已知),
(平角定义).
又(已知),
(同角的补角相等).
又(已知),
(等量代换).
(内错角相等,两直线平行).
(两直线平行,内错角相等).
故答案为:1;平角定义;1;同角的补角相等;3;等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
22. 已知关于,的二元一次方程组,其中为实数.
(1)当时,求方程组的解;
(2)求的值(用含的代数式表示);
(3)试说明无论取何数时,代数式的值始终不变.
【答案】(1)
(2)
(3)见解析
【解析】
【分析】本题主要考查了解二元一次方程组和方程组的解,解题关键是熟练掌握解二元一次方程组的一般步骤和方程组解的定义.
(1)把代入关于,的二元一次方程组得关于,的方程组,解方程组求出,即可;
(2)把两个方程相加,求出即可;
(3)把方程②①,消去,从而得到的值,从而求出的值即可.
【小问1详解】
把代入关于,的二元一次方程组得:,
①②得:,
把代入②得:,
方程组的解为:,
当时,方程组的解为:;
【小问2详解】
,
①②得:,
,
;
【小问3详解】
证明:,
②得:③,
①③得:,
,
,
无论取何数时,代数式的值始终不变.
23. 如图,已知,在△ABC中,AH平分∠BAC交BC于点H,D,E分别在CA,BA的延长线上,DBAH,∠D=∠E.
(1)求证:DBEC;
(2)若∠ABD=2∠ABC,∠DAB比∠AHC大12°,求∠D的度数.
【答案】(1)见解析 (2)48°
【解析】
【分析】(1)根据平行线的性质可得∠D=∠CAH,根据角平分线的定义可得∠BAH=∠CAH,再根据已知条件和等量关系可得∠BAH=∠E,再根据平行线的判定即可求解;
(2)可设∠ABC=x,则∠ABD=2x,则∠BAH=2x,可得∠DAB=180°−4x,可得∠AHC=168°−4x,可得168°−4x=3x,解方程求得x,进一步求得∠D的度数.
【小问1详解】
∵DB∥AH,
∴∠D=∠CAH,
∵AH平分∠BAC,
∴∠BAH=∠CAH,
∵∠D=∠E,
∴∠BAH=∠E,
∴DB∥EC;
【小问2详解】
设∠ABC=x,则∠ABD=2x,
则∠BAH=2x,则∠DAB=180°-4x,
则∠AHC=168°-4x,
依题意有168°-4x=3x,
解得x=24°,
则∠D=180°-2x-(180°-4x)=2x=48°.
【点睛】本题考查了三角形内角和定理,角平分线的定义,平行线的判定与性质,熟练掌握知识点是解题的关键.
24. 在平面直角坐标系中,对于点,若点Q的坐标为,则称点Q是点P的“a阶派生点”(其中a为常数,且).例如:点的“2阶派生点”为点,即点.
(1)若点P的坐标为,则它的“3阶派生点”的坐标为________;
(2)若点P的“5阶派生点”的坐标为,求点P的坐标;
(3)若点P先向左平移2个单位长度,再向上平移1个单位长度后得到了点,点的“阶派生点”位于坐标轴上,求点P2的坐标.
【答案】(1)
(2)
(3)或
【解析】
【分析】(1)根据派生点的定义,结合点的坐标计算后即可得出结论;
(2)根据派生点的定义,结合点的坐标列出二元一次方程组,计算后即可得出结论;
(3)先根据点的平移特点得出点的坐标为,再由派生点的定义和点的“阶派生点”位于坐标轴上,分在轴和轴上,两种情况进行讨论求解即可.
【小问1详解】
解:根据新定义,点P的“3阶派生点”的坐标为
即:;
∴点的“3阶派生点”的坐标为.
【小问2详解】
由题意,得:,
解得:,
∴点P的坐标为;
【小问3详解】
∵点先向左平移2个单位长度,再向上平移1个单位长度后得到了点
∴点
∴的“阶派生点”为:
即
当点在x轴上
,
解得:;
此时;
当点在y轴上
,
解得:;
此时;
∴点的坐标或.
【点睛】本题考查了新定义下求点的坐标,平移的坐标表示等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
25. 在平面直角坐标系中,,,且、满足.
(1)填空: , ;
(2)如图1,点,若三角形的面积为三角形的面积的2倍,求点的坐标;
(3)如图2,若将线段平移至,点、也在坐标轴上,点为线段上的一动点,
①若为直线、之间的一个点,直接写出、、之间的数量关系;
②连接,若平分,,求式子的值.
【答案】(1)2,
(2)或
(3)①.②
【解析】
【分析】(1)根据非负数的性质即可求出与的值.
(2)由(1)可知:,,所以,,所以,从而可求出,然后根据点的位置分类讨论,列出关于的方程即可求出答案.
(3)①过点作直线交轴于点,根据平行线的性质即可求出、、之间的数量关系.
②延长交直线于点,设,,根据平行线的性质、三角形外角的性质即可求出,,最后代入原式即可求出答案.
【小问1详解】
,
,,
解得:,.
故答案为:2,;
【小问2详解】
由(1)可知:,,
,,,
,
,
当位于轴下方时,
,
,
,
,
当位于轴上方时,
,
,
,
,
或.
【小问3详解】
①过点作直线交轴于点,
,
,,
.
②延长交直线于点,
设,,
由①可知:,
,
,
,
,
.
【点睛】本题是三角形综合题,考查了非负数的性质,三角形的外角的性质,平行线的性质,三角形的面积公式等,熟练掌握以上知识是解题的关键.
福建省厦门市槟榔中学2023-2024学年七年级下学期期中数学试题(原卷版+解析版): 这是一份福建省厦门市槟榔中学2023-2024学年七年级下学期期中数学试题(原卷版+解析版),文件包含福建省厦门市槟榔中学2023-2024学年七年级下学期期中数学试题原卷版docx、福建省厦门市槟榔中学2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
福建省厦门市莲花中学2023-2024学年七年级下学期期中数学试题(原卷版+解析版): 这是一份福建省厦门市莲花中学2023-2024学年七年级下学期期中数学试题(原卷版+解析版),文件包含福建省厦门市莲花中学2023-2024学年七年级下学期期中数学试题原卷版docx、福建省厦门市莲花中学2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
福建省厦门市湖滨中学2023-2024学年七年级下学期期中数学试题(原卷版+解析版): 这是一份福建省厦门市湖滨中学2023-2024学年七年级下学期期中数学试题(原卷版+解析版),文件包含福建省厦门市湖滨中学2023-2024学年七年级下学期期中数学试题原卷版docx、福建省厦门市湖滨中学2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












