四川省广元市苍溪县2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份四川省广元市苍溪县2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含四川省广元市苍溪县2023-2024学年七年级下学期期中数学试题原卷版docx、四川省广元市苍溪县2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。

一、选择题（共10小题，每小题3分，共30分）
1. 下列图形中，和是同位角的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】本题主要考查了同位角的定义．根据同位角是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角，即可求解．
【详解】解：由同位角的定义得：第一个图中的和是同位角，其余选项都不是同位角，
故选：A．
2. 下列命题：邻补角互补；有理数是有限小数，无理数是无限小数；过一点有且只有一条直线与这条直线平行；实数与数轴上的点一一对应；不带根号的数一定是有理数．其中真命题的有（ ）．
A. 个B. 个C. 个D. 个
【答案】B
【解析】
【分析】本题考查了命题的真假判断，根据邻补角的性质、有理数的定义、平行公理、实数与数轴的关系逐一判断即可求解，掌握相关知识点是解题的关键．
【详解】解：邻补角互补，该命题是真命题，符合题意；
有理数包括了整数和分数，无理数是无限不循环小数，该命题是假命题，不合题意；
过直线外一点有且只有一条直线与这条直线平行，该命题是假命题，不合题意；
实数与数轴上的点一一对应，该命题是真命题，符合题意；
不带根号的数不一定是有理数，比如和含的式子，该命题是假命题，不合题意；
∴真命题的有，共个，
故选：．
3. 如图，将直尺与含角的三角尺叠放在一起，角的顶点落在直尺的一边上，其两边与直尺相交，若，则的度数是（ ）

A. B. C. D.
【答案】B
【解析】
【分析】本题考查了平行线的性质，三角板中角度的计算，根据两直线平行，同旁内角互补得出，即可求出的度数，结合含角的三角尺即可求出的度数．
【详解】解：如图，

，
，
，
，
由题意得，
，
故选：B．
4. 在实数、、、、、（1和3之间的2逐次加1个）中，无理数的个数为（ ）
A. 2个B. 3个C. 4个D. 5个
【答案】C
【解析】
【分析】本题考查无理数，掌握无限不循环的小数是无理数是正确判断的前提．
根据无理数的定义逐个数进行判断得出答案．
【详解】解：3.1415、是有理数，
，，，和3之间的2逐次加1个）是无理数，共有4个，
故选：C．
5. 点所在的象限是（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
【答案】A
【解析】
【分析】平面直角坐标系中每个象限的点的特征，第一象限（＋，＋），第二象限（－，＋），第三象限（－，－），第四象限（＋，－），分析判断即可得出答案．
【详解】横纵坐标都为正数，故在第一象限，
故选A．
【点睛】本题考查了平面直角坐标系中每个象限的点的特征，掌握此概念是本题的关键．
6. 如图，若，则 （ ）

A. B. C. D.
【答案】B
【解析】
【分析】本题考查了平行线的性质与判定；先证明，进而根据邻补角求得，进而根据平行线的性质，即可求解．
【详解】解：如图所示，

∵，
∴，
∵，
∴，
，
故选：B．
7. 如图，已知正方形的面积为5，顶点A在数轴上，且表示的数为1．现以A为圆心，为半径画圆，与数轴交于点E（E在A的右侧），则点E表示的数为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题主要考查实数与数轴及两点间距离，根据正方形的边长是面积的算术平方根得，结合A 点所表示的数及间距离可得点E所表示的数，根据两点间距离及点的位置判断出点所表示的数是关键．
【详解】解：∵正方形的面积为5，且，
∴，
∵点A表示的数是1，且点E在点A的右侧，
∴点E表示的数为．
故选：D．
8. 象棋起源于中国，中国象棋文化历史悠久．如图，是中国象棋棋盘的一部分，若“帅”位于点，“炮”位于点上，则“兵”位于点（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了根据点的位置求点的坐标，根据纵坐标在上用加法，横坐标在左用减法，即可求出“兵”的坐标，解题的关键是找到点所对应的横坐标和纵坐标，再写出点的坐标．
【详解】解：∵“兵”在“炮”的上面一行，
∴“兵“的纵坐标是，
∵“兵”在“帅”的左面第二格上，
∴“兵”的横坐标是，
∴“兵”的坐标是，
故选：．
9. 如图，沿射线方向平移到（点在线段上）．若，，则平移距离为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据平移的性质有：，则有，即有，根据，问题得解．
【详解】根据平移的性质有：，
∴，
∴，
∴，
∵，，
∴，
∴则平移距离为，
故选：A．
【点睛】本题主要考查了图形的平移，根据平移的性质得到，是解答本题的关键．
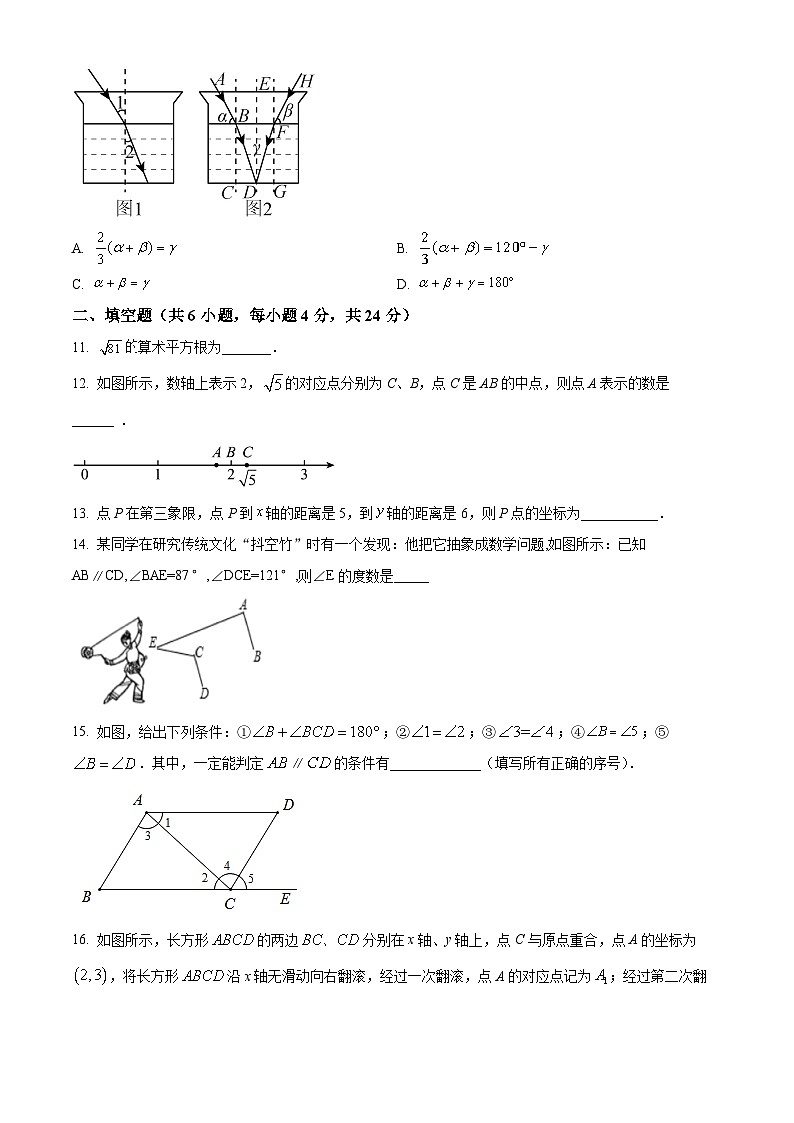
10. 如图1，当光线从空气斜入射到某种透明的液体时发生了折射，满足入射角与折射角的度数比为．如图2，在同一平面上，两条光线同时从空气斜射入这种液体中，两条入射光线与水平液面夹角分别为，，在液体中两条折射光线的夹角为，则，，三者之间的数量关系为（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】过点B、D、F分别作水平线的垂线，则，根据平行线的性质与光的折射原理即可得到答案
【详解】如图：过点B、D、F分别作水平线的垂线，则
由题知



即：
即
故选B
【点睛】本题考查了平行线的性质，光学原理，读懂题并熟练掌握平行线的性质是关键．
二、填空题（共6小题，每小题4分，共24分）
11. 的算术平方根为_______．
【答案】
【解析】
【分析】先计算，在计算9的算术平方根即可得出答案．
【详解】，9的算术平方根为
的算术平方根为．
故答案为：．
【点睛】本题考查了算术平方根，熟练掌握算术平方根的概念是解题的关键．
12. 如图所示，数轴上表示2，对应点分别为C、B，点C是AB的中点，则点A表示的数是______ ．

【答案】##-+4
【解析】
【详解】∵数轴上表示2，的对应点分别为C、B，
∴BC=−2，
∵点C是AB的中点，
∴AC=BC=−2，
∴点A表示的数为2−(−2)=4−，
故答案为：4−.
13. 点P在第三象限，点P到轴的距离是5，到轴的距离是6，则P点的坐标为___________．
【答案】（-6，-5）
【解析】
【分析】根据点到坐标轴是距离解答．
【详解】解：∵点P在第三象限，点P到轴的距离是5，到轴的距离是6，
∴P点的坐标为（-6，-5），
故答案：（-6，-5）．
【点睛】此题考查了点到坐标轴的距离，解题的关键是掌握点到x轴的距离是点纵坐标的绝对值，点到y轴的距离是点横坐标的绝对值，还考查了象限内点的坐标符号．
14. 某同学在研究传统文化“抖空竹”时有一个发现：他把它抽象成数学问题,如图所示：已知AB∥CD,∠BAE=87°,∠DCE=121°,则∠E的度数是_____
【答案】34°
【解析】
【分析】延长DC交AE于F，依据AB∥CD，∠BAE=87°，可得∠CFE=87°，再根据三角形外角性质，即可得到∠E=∠DCE-∠CFE．
【详解】如图，延长DC交AE于F，
∵AB∥CD,∠BAE=87°，
∴∠CFE=87°，
又∵∠DCE=121°，
∴∠E=∠DCE−∠CFE=121°−87°=34°，
故答案为34°
【点睛】此题考查平行线的性质，三角形外角性质，解题关键在于作辅助线.
15. 如图，给出下列条件：①；②；③；④；⑤．其中，一定能判定∥的条件有_____________（填写所有正确的序号）．
【答案】①③④
【解析】
【分析】根据平行线的判定方法对各小题判断即可解答．
【详解】① ∵，
∴∥（同旁内角互补，两直线平行），正确；
② ∵，
∴∥，错误；
③ ∵，
∴∥（内错角相等，两直线平行），正确；
④ ∵，
∴∥（同位角相等，两直线平行），正确；
⑤ 不能证明∥，错误，
故答案为：①③④．
【点睛】本题考查了平行线的判定，熟练掌握平行线的判定方法是解答的关键．
16. 如图所示，长方形的两边分别在x轴、y轴上，点C与原点重合，点A的坐标为，将长方形沿x轴无滑动向右翻滚，经过一次翻滚，点A的对应点记为；经过第二次翻滚，点A的对应点记为；……依次类推，经过第2022次翻滚，点A的对应点的坐标为______．

【答案】
【解析】
【分析】本题考查探究点的坐标的规律问题，关键是找到点的变化规律．观察图形即可得到经过4次翻滚后点对应点一次循环，先求出的商和余数，从而解答本题．
【详解】解：如图所示：
观察图形可得经过4次翻滚后点对应点一循环，
，
点，长方形的周长为：，
经过505次翻滚后点对应点的坐标为，即．
故答案为：．
三、解答题（共10小题，共96分）
17. 计算：
（1）
（2）
【答案】（1）
（2）
【解析】
【分析】本题考查实数的运算，
（1）根据立方根，绝对值的代数意义和算术平方根将原式化简，再进行加减运算；
（2）根据绝对值的代数意义，算术平方根及立方根将原式化简，再进行加减运算；
掌握相应的定义，运算法则和性质是解题的关键
【小问1详解】
解：
；
【小问2详解】
．
18. 已知：与是某正数的两个不相等的平方根，的立方根是．求：
（1）的值；
（2）的算术平方根．
【答案】（1），
（2）4
【解析】
【分析】（1）根据平方根与立方根的定义即可求出答案．
（2）先求出，再计算算术平方根即可．
【小问1详解】
解：由题意可知：，
，
的立方根为，
，
；
【小问2详解】
由（1）可知：，，
，
的算术平方根是4．
【点睛】本题考查平方根与立方根，解题的关键是熟练运用平方根与立方根的定义，本题属于基础题型．
19. 已知：如图，在直角中，，点D为线段上一点，过点D作，垂足为E；过点D作，交于点F．
（1）依题意补全图形；
（2）请你判断与的数量关系，并加以证明．
【答案】（1）见解析 （2），证明见解析
【解析】
【分析】（1）按要求作图即可；
（2）根据得到，再根据平行线的性质得到，等量代换即可证明．
【小问1详解】
解：如图所示：
【小问2详解】
∵，
∴，
∵，
∴，
∴．
【点睛】本题主要考查了垂线的定义，平行线的性质，能综合应用这些定理是解题的关键．
20. 如图，一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B，点A表示，设点B所表示的数为m．
（1）求的值：
（2）在数轴上还有C、D两点分别表示实数c和d，且有与互为相反数，求的平方根．
【答案】（1）3 （2）
【解析】
【分析】（1）利用两点间的距离公式求出m的值，然后代入代数式计算即可；
（2）利用非负数的性质得到c，d的值，代入代数式求值得到平方根．
【小问1详解】
解：∵，
∴，
∴，
∴
；
【小问2详解】
∵与互为相反数，
∴，
∴，，
∴，，
∴，
则的平方根为．
【点睛】本题主要考查数轴上两点之间的距离、绝对值的意义、绝对值和根号的非负性、平方根以及有理数的混合运算，解题的关键是利用两点之间的距离和非负性求得字母的值．
21. 如图，于，点是上任意一点，于，且，．
（1）试证明；
（2）分别求，的度数．
【答案】（1）证明见解析；
（2），．
【解析】
分析】（）证明，得到，再得到，即得，得到，即可求证；
（）由得到，再根据邻补角的性质可得；
本题考查了平行线的判定和性质，邻补角的性质，掌握平行线的判定和性质是解题的关键．
【小问1详解】
证明：∵，，
∴，，
∴，
∴，
∴，
∵，
∴，
∴，
∴；
【小问2详解】
解：∵，
∴，
∵，
∴，
又∵，
∴．
22. 如图，在直角坐标平面内，已知点A的坐标（－4，0），点A关于y轴对称的点为点C．
（1）请求出点C坐标，并在网格图中标出点A和点C．
（2）求△ABC的面积；
（3）在y轴上找一点D，使S△ACD＝S△ABC，请直接写出点D的坐标．
【答案】（1）
，图见解析
（2）16 （3）或
【解析】
【分析】本题考查了轴对称的性质，坐标与图形，三角形的面积等知识；
（1）先根据关于轴对称的点横坐标互为相反数，纵坐标相同求出点的坐标，再在坐标系中描出、即可；
（2）根据进行求解即可；
（3）先根据三角形面积求出点的纵坐标，再根据在轴上的点横坐标为0即可得到答案．
【小问1详解】
解：点的坐标为，点关于轴对称的点为，
，如下图所示，点、即为所求；
【小问2详解】
解：，
，
，
；
【小问3详解】
解：,
，
，
或，
又在轴上，
点的坐标为或．
23. 如图，已知：中，分别在和上，连接和，，．
（1）判断与的位置关系，并证明；
（2）若，，求的度数．
【答案】（1），证明见解析；
（2）．
【解析】
【分析】（）．由可明，得到，进而由得，即可求证；
（）由，，可得，，再由垂直得，利用角的和差关系即可求解；
本题考查了平行线的判定和性质，垂直的定义，掌握平行线的判定和性质是解题的关键．
【小问1详解】
解：，理由如下：
，
，
，
又，
，
；
【小问2详解】
解：由（）可知，，，
，
，
，
，
，
．
24. 如图，面积为的正方形的边在数轴上，点B表示的数为1．将正方形沿着数轴水平移动，移动后的正方形记为，点A，B，C，D的对应点分别为，，，，移动后的正方形与原正方形重叠部分图形的面积记为S．
（1）当正方形向右移动1时，求：移动后的正方形与原正方形重叠部分图形的面积；
（2）当时时，用含a的代数式表示数轴上点表示的数．
【答案】（1）
（2）或
【解析】
【分析】本题主题考查了实数与数轴：
（1）当正方形向右移动1时，如图1，求出即可算出重叠部分的面积；
（2）平移可分为两种情况，向右平移和向左平移，根据面积求出边长，求出平移距离，即可得出答案．
【小问1详解】
当正方形向右移动1时，如图1，
∵正方形的面积为，
∴，
∴，
∴重叠部分图形的面积；
【小问2详解】
解：当向右移动时，如图2，
∵重叠部分图形的面积，
∴，
∴，
∴，
∴点表示的数是；
当向左移动时，如图3，
∵重叠部分图形的面积，
∴，
∴，
∴，
∴点表示的数是；
综上所述，点表示数是或．
25. 问题探究：
如图①，已知，我们发现．我们怎么证明这个结论呢？嘉嘉同学：如图②，过点E作，把分成与的和，然后分别证明，．淇淇同学：如图③，过点B作交的延长线于点G，然后再证明，．
问题解答：（1）请按淇淇同学的思路，写出证明过程；
问题迁移：（2）如图④，已知，平分，平分，若，请直接写出的度数．
【答案】（1）见解析；（2）．
【解析】
【分析】本题主要考查平行线的性质，解题的关键是学会添加常用辅助线，利用平行线的性质解决问题．
（1）如图③中，过点B作交的延长线于G，利用平行线的性质求出，，，根据证明即可；
（2）设，，则，求出，，根据，构建方程求出可得结论．
【详解】证明：（1）如图③中，过点B作交的延长线于G．
∵，
∴，，
∵，
∴，
∴，
∴；
（2）如图④中，
∵平分，平分，
∴，，
设，，则，
∵，
∴，
∵，
∴，
∵，
∴，
∴，
∴．
26. 在平面直角坐标系中，O为原点，点，，．
（1）如图①，则三角形的面积为 ；
（2）如图②，将点B向右平移7个单位长度，再向上平移4个单位长度，得到对应点D．
①求三角形的面积；
②点是一动点，若的面积等于的面积．请直接写出点P坐标．
【答案】（1）6 （2）①9；②或．
【解析】
【分析】本题考查了坐标与图形、点的平移、绝对值方程等知识，掌握运用数形结合的思想分析解决问题是解题关键．
（1）根据题意得出，，，然后根据三角形面积公式直接计算即可；
（2）①连接，过点作轴于点，过点作轴于点，由平移的性质可得点坐标，根据进行计算即可得到答案；②根据的面积等于的面积，求解即可．
【小问1详解】
解：∵，，，
∴，，，
∴，
∴．
故答案为：6；
【小问2详解】
解： ①连接，过点作轴于点，过点作轴于点，
将点向右平移7个单位长度，再向上平移4个单位长度，得到对应点坐标为

∴，，
∴
；
②如下图，

根据题意，点，且，
即有，
解得，
∴点坐标为或．