2024年吉林省长春市宽城区中考一模数学试题（原卷版+解析版）

这是一份2024年吉林省长春市宽城区中考一模数学试题（原卷版+解析版），文件包含2024年吉林省长春市宽城区中考一模数学试题原卷版docx、2024年吉林省长春市宽城区中考一模数学试题解析版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。

一、选择题（本大题共8小题，每小题3分，共24分）
1. 如图，比数轴上点表示的数大2的数是（ ）
A. B. 0C. 1D. 2
2. 据海关统计，2024年月长春市进出口总额约215.4亿元．数据215.4亿用科学记数法表示为（ ）
A. B. C. D.
3. 不等式的解集在数轴上表示正确的是（ ）
A. B.
C. D.
4. 如图，裁掉一个正方形后能折叠成正方体，但不能裁掉的是（ ）
A. ①B. ②C. ③D. ④
5. 如图，直线，点、分别在、上，以点为圆心，长为半径作弧，交于点，连结．若，则的大小为（ ）
A. B. C. D.
6. 如图，某校无人机兴趣小组借助无人机测量教学楼的高度，在离教学楼底部处米的处，无人机垂直上升米至处，测得教学楼顶处的俯角为，则教学楼的高度为（ ）
A. 米B. 米
C. 米D. 米
7. 如图，四边形内接于，延长至点．若，则的大小为（ ）
A. B. C. D.
8. 如图，在平面直角坐标系中，正方形的顶点在直线上，顶点在函数的图象上，、两点在轴上．若点的横坐标为，则的值为（ ）
A. 6B. C. 12D.
二、填空题（本大题共6小题，每小题3分，共18分）
9. 分解因式：___．
10. 若关于的方程有实数根，且为正整数，则的值是________．
11. 如图，将绕点A逆时针旋转得到，点的对应点为．若，，则的大小为________度．
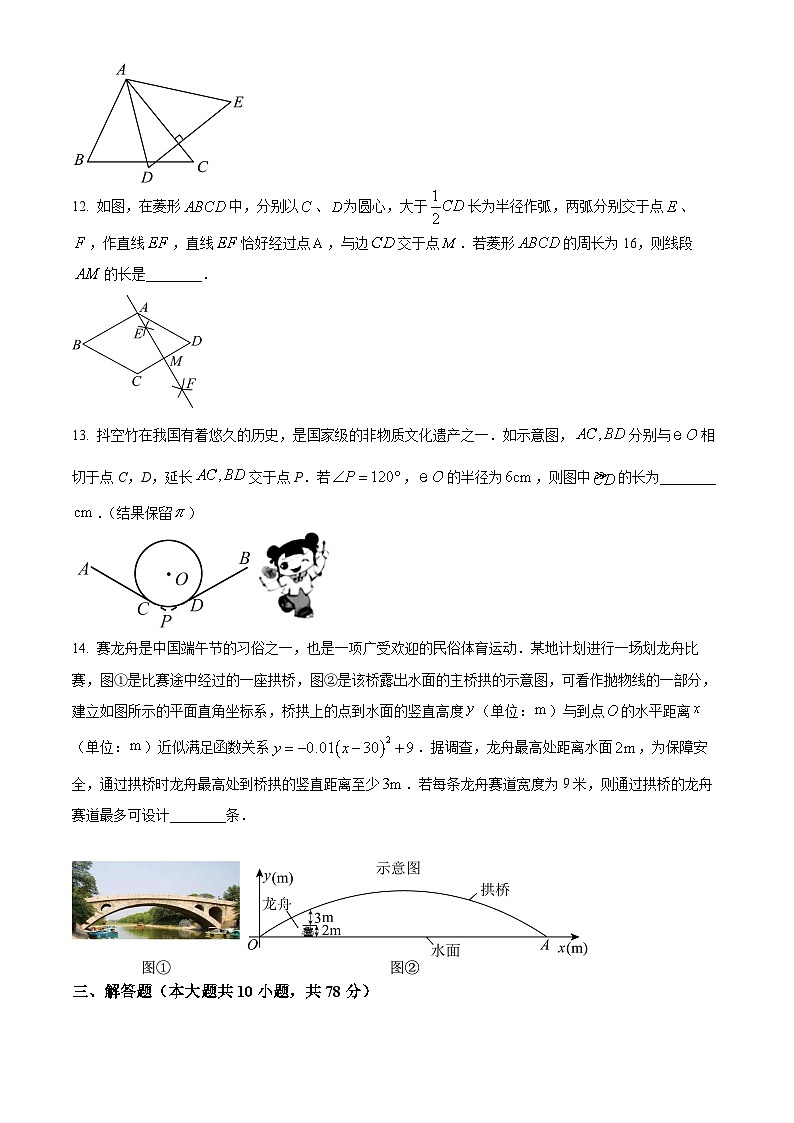
12. 如图，在菱形中，分别以、为圆心，大于长为半径作弧，两弧分别交于点、，作直线，直线恰好经过点，与边交于点．若菱形的周长为16，则线段的长是________．
13. 抖空竹在我国有着悠久的历史，是国家级的非物质文化遗产之一．如示意图，分别与相切于点C，D，延长交于点P．若，的半径为，则图中的长为________．（结果保留）
14. 赛龙舟是中国端午节的习俗之一，也是一项广受欢迎的民俗体育运动．某地计划进行一场划龙舟比赛，图①是比赛途中经过的一座拱桥，图②是该桥露出水面的主桥拱的示意图，可看作抛物线的一部分，建立如图所示的平面直角坐标系，桥拱上的点到水面的竖直高度（单位：）与到点的水平距离（单位：）近似满足函数关系．据调查，龙舟最高处距离水面，为保障安全，通过拱桥时龙舟最高处到桥拱的竖直距离至少．若每条龙舟赛道宽度为9米，则通过拱桥的龙舟赛道最多可设计________条．
三、解答题（本大题共10小题，共78分）
15. 先化简，再求值：，其中，．
16. 二十四节气是中国古代一种用来指导农事的补充历法，在国际气象界被誉为“中国的第五大发明”，并位列联合国教科文组织人类非物质文化遗产代表作名录．小红和小丽对二十四节气非常感兴趣，在课间玩游戏时，准备了四张完全相同的不透明卡片，卡片正面分别写有“A惊蛰”、“B春分”、“C谷雨”、“D立夏”四个节气，两人商量将卡片背面朝上洗匀后，从中随机抽取一张，并讲述所抽卡片上的节气的由来与习俗．小红先从四张卡片中随机抽取一张，小丽再从剩下的卡片中随机抽取一张，请用画树状图（或列表）的方法，求两人都没有抽到“C谷雨”的概率．
17. 某服装厂要给光明中学制作套校服，为了尽快完成任务，实际每天制作校服的数量比原计划每天多了，结果提前天完成任务，求原计划每天制作校服的套数．
18. 图①、图②、图③均是的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，线段的端点均在格点上．只用无刻度的直尺，在给定的网格中，分别按下列要求画图，保留适当的作图痕迹，不要求写出画法．
（1）在图①中画一个等腰直角，使其面积为．
（2）在图②中画一个等腰锐角，使其面积为．
（3）在图③中画一个，使其面积，且．
19. 如图，在中，D是的中点，E是的中点，过点A作交的延长线于点F．

（1）求证：；
（2）连接，若，求证：四边形是矩形．
20. 6月5日是世界环境日，为了提高学生的环保意识，某校七、八年级举行了环保知识竞赛，全体学生参加比赛．为了解学生的答题情况，学校从这两个年级中各随机抽取10名学生的成绩（满分100分）进行整理分析，得到如下信息：
七、八年级各抽取的10名学生成绩的平均数、中位数、众数如下：
根据以上信息，解答下列问题：
（1）表中________，________．
（2）七、八年级各抽取这10名学生成绩的方差分别记为、，请判断________．（填“>”“<”或“=”）
（3）若规定成绩85分及以上为优秀，七、八年级各有200名学生，请估计该校七、八年级学生中成绩为优秀的总人数．
21. 为丰富学生体育活动的内容，某学校计划到甲、乙两个体育专卖店购买一批新的体育用品，两个专卖店的优惠活动如下：
甲：所有商品按原价八折出售；
乙：一次购买商品总额不超过一定金额时按原价付款，超过其一定金额的部分享受打折优惠．
设需要购买体育用品的原价总额为元，实际付款为元，其函数图象如图所示．
当时，在甲、乙两个专卖店购买商品实际付款相同．
（1）当时，________．
（2）当在乙专卖店一次购买商品有打折优惠时，求与之间的函数关系式，并直接写出打几折出售．
（3）当在甲、乙两个专卖店一次购买商品的原价总额相同，而实际付款相差20元时，直接写出的值．
22. 【性质结论】如图①，在中，，是斜边的中线，则与的数量关系为________．
【性质应用】如图②，在中，，为边上一点（点不与点、重合），于点，点为的中点，连结、、．
（1）求证：．
（2）若，则的大小为________度．
【性质延伸】如图③，在四边形中，，，，．在四边形内存在一点，点到四边形四个顶点的距离均为，则的值为________．
23. 如图，在中，，，，点在边上，且．点从点出发沿边向终点运动，点关于所在直线的对称点为，连接、．
（1）求线段长．
（2）点与点的最短距离为________．
（3）当点落在内部时，求线段长的取值范围．
（4）当所在直线与的某一条边垂直时，直接写出线段的长．
24. 在平面直角坐标系中，顶点坐标为的抛物线经过点，与轴相交于点．点在这条抛物线上运动，其横坐标为．
（1）求这条抛物线所对应的函数表达式及点的坐标．
（2）当点在、两点之间（点不与点、重合）运动时，过点作轴的平行线交线段于点．当线段的长随的增大而减小时，求的取值范围．
（3）当抛物线在、两点之间（包含、两点）函数的最小值为，求的值．
（4）当点不与点重合时，以为对角线作矩形，使轴．设直线将矩形的面积分为、两部分，当时，直接写出的取值范围．年级
平均数
中位数
众数
七年级
85.5
87
八年级
855
85