2024年河南省中考数学三轮复习冲刺模拟练习试卷（原卷+解析）

这是一份2024年河南省中考数学三轮复习冲刺模拟练习试卷（原卷+解析），文件包含2024年河南省中考数学三轮复习冲刺模拟练习试卷解析版docx、2024年河南省中考数学三轮复习冲刺模拟练习试卷docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

选择题（本大题共有10个小题，每小题3分，共30分）
1. 故宫又称紫禁城，位于北京中轴线的中心，占地面积高达平方米，
在世界宫殿建筑群中面最大．请将用科学记数法表示应为（ ）

A．B．C．D．
【答案】B
【分析】把一个大于的数记成的形式，其中是整数数位只有一位的数，是正整数，
这种记数法叫做科学记数法，由此即可得到答案．
【详解】解：将用科学记数法表示应为，故B正确．
故选：B．
2 . 下列运算正确的是（ ）
A．B．C．D．
【答案】C
【分析】根据合并同类项，同底数幂的除法，同底数幂的乘法，积的乘方以及完全平方公式逐项计算即可．
【详解】解：A.2a与3b不是同类项，不能合并，故不正确；
B. ，故不正确；
C. ，故正确；
D. ，故不正确；
故选C．
3. 下列图形中，既是轴对称又是中心对称图形的是（ ）
A．B．C．D．
【答案】A
【分析】根据轴对称图形与中心对称图形的概念结合各图形的特点求解．
【详解】A、是轴对称图形，也是中心对称图形，故本选项符合题意，
B、是轴对称图形，不是中心对称图形，故本选项不合题意，
C、不是轴对称图形，是中心对称图形，故本选项不合题意，
D、是轴对称图形，不是中心对称图形，故本选项不合题意，
故选：A．
4. 计算的结果等于（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据异分母分式加减法法则进行计算即可．
【详解】解：
；
故选：C．
每年的4月23日是“世界读书日”．某中学为了了解八年级学生的读数情况，
随机调查了50名学生的册数，统计数据如表所示：
则这50名学生读书册数的众数、中位数是（ ）
A．3，3B．3，2C．2，3D．2，2
【答案】B
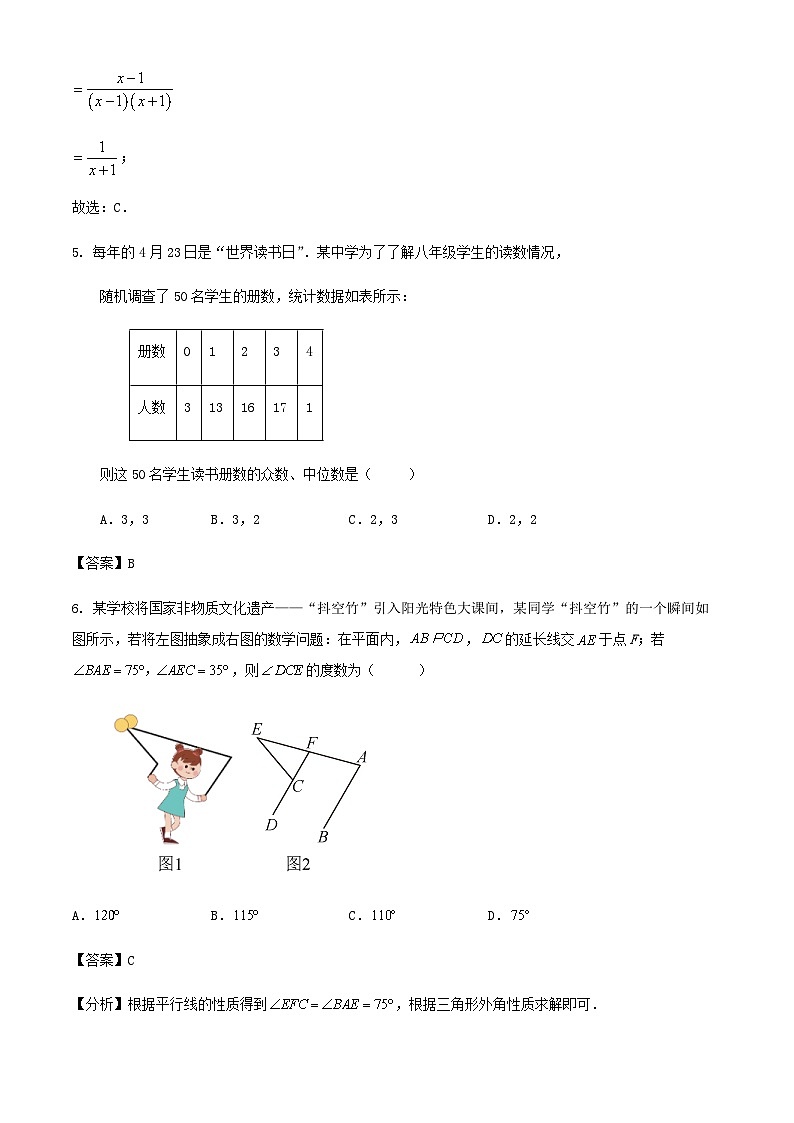
6. 某学校将国家非物质文化遗产——“抖空竹”引入阳光特色大课间，某同学“抖空竹”的一个瞬间如图所示，若将左图抽象成右图的数学问题：在平面内，，的延长线交于点F；若，则的度数为（ ）

A．B．C．D．
【答案】C
【分析】根据平行线的性质得到，根据三角形外角性质求解即可．
【详解】解：∵，，
∴，
∵，
∴，
故选：C．
7. 关于x的一元二次方程 （k为实数）根的情况是（ ）
A．有两个不相等的实数根B．有两个相等的实数根
C．方程没有实数根D．不能确定
【答案】A
【分析】根据一元二次方程根的判别式即可判断根的情况．
【详解】
∴方程有两个不相等的实数根．
故选：A．
8 . 赵州桥是当今世界上建造最早，保存最完整的中国古代单孔敞肩石拱桥.如图，主桥拱呈圆弧形，
跨度约为，拱高约为，则赵州桥主桥拱半径R约为（ ）

A. B. C. D.
【答案】B
【解析】
【分析】由题意可知，，，主桥拱半径R，根据垂径定理，得到，再利用勾股定理列方程求解，即可得到答案．
【详解】解：如图，由题意可知，，，主桥拱半径R，
，
是半径，且，
，
在中，，
，
解得：，
故选B

9. 如图，ABCD是一张矩形纸片，点E是AD边上的一点，将纸片沿直线BE翻折，
点A落在DC边上的点F处，若AB＝10，AD＝8，则DE的长为（ ）

A．6B．5C．4D．3
解：∵四边形ABCD是矩形，AB＝10，AD＝8
∴，，
∵将纸片沿直线BE翻折，点A落在DC边上的点F处
∴，
在中，
∴
设
∴
在中，
∴，解得
∴，
故选：D．
10 . 如图，已知开口向上的抛物线与轴交于点，对称轴为直线．下列结论：
①；②；③若关于的方程一定有两个不相等的实数根；④.
其中正确的个数有（ ）

A．1个B．2个C．3个D．4个
【答案】D
【分析】利用二次函数图象与性质逐项判断即可．
【详解】解：∵抛物线开口向上，
∴，
∵抛物线与y轴交点在负半轴，
∴，
∵对称轴为，
∴，
∴，
故①正确；
∵抛物线的对称轴为，
∴，
∴，
故②正确；
∵函数与直线有两个交点．
∴关于的方程一定有两个不相等的实数根，
故③正确；
∵时，即，
∵，
∴，即，
∵，
∴，
∴，
故④正确，
故选：D
填空题（本大题共有5个小题，每小题3分，共15分）
11 现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片，
卡片除正面图案不同外，其余均相同，将三张卡片正面向下洗匀，从中随机抽取一张卡片，
则抽出的卡片图案是琮琮的概率是 ．

【答案】
【分析】根据概率公式即可求解．
【详解】解：将三张卡片正面向下洗匀，从中随机抽取一张卡片，
则抽出的卡片图案是琮琮的概率是
故答案为：．
12. 若关于的方程有两个不相等的实数根，则的取值范围为 .
【答案】且
【分析】根据方程有两个不相等的实数根得到，且，求解即可．
【详解】解：∵方程有两个不相等的实数根，
∴，且，
解得且，
故答案为：且．
13. 如图，正六边形ABCDEF的边长为2，以顶点A为圆心，AB的长为半径画圆，
则图中阴影部分的面积为 ．

【答案】
【分析】延长FA交⊙A于G，如图所示：根据六边形ABCDEF是正六边形，AB=2，利用外角和求得∠GAB=，再求出正六边形内角∠FAB=180°-∠GAB=180°-60°=120°， 利用扇形面积公式代入数值计算即可．
【详解】解：延长FA交⊙A于G，如图所示：
∵六边形ABCDEF是正六边形，AB=2，
∴∠GAB=，
∠FAB=180°-∠GAB=180°-60°=120°，
∴，
故答案为．
14. 某快递公司每天上午为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量（件）与时间（分）之间的函数图象如图所示，那么从开始，
经过______分钟时，当两仓库快递件数相同．

【答案】20
【分析】利用待定系数法分别求出甲、乙两仓库的快件数量（件）与时间（分）之间的函数关系式，在求出两直线的交点即可得到答案．
【详解】解：设甲仓库的快件数量（件）与时间（分）之间的函数关系式为，
根据图象得，，
解得：，
，
设乙仓库的快件数量（件）与时间（分）之间的函数关系式为，
根据图象得，，
解得：，
，
联立，
解得：，
经过20分钟时，当两仓库快递件数相同，
故答案为：20．
15 .如图，在矩形ABCD中，AB=8，BC=12，点E是BC的中点，连接AE，
将△ABE沿AE折叠，点B落在点F处，连接FC，则sin∠ECF=__________．

【答案】
解：过E作EH⊥CF于H，
则有∠HEC+∠ECH=90°，
由折叠的性质得：BE=EF，∠BEA=∠FEA，
∵点E是BC的中点，
∴CE=BE，
∴EF=CE，
∴∠FEH=∠CEH，
∴∠AEB+∠CEH=90°，
∴∠ECH=∠AEB，即∠ECF=∠AEB，
在矩形ABCD中，
∵∠B=90°，
∴ AE==10，
∴sin∠ECF=sin∠AEB= = ，
故答案为．
三、解答题（本大题共8个小题，共75分．解答应写出文字说明，证明过程或演算步骤）
16. （1）计算：－tan60°；
（2）化简：．
【答案】（1）-2；（2）
【分析】（1）先化简二次根式，绝对值，计算负整数指数幂，特殊角的三角函数值，再合并即可；
（2）先计算括号内的分式的减法，再把除法转化为乘法运算，约分后可得结果．
【详解】解：（1）－tan60°
=2+1－－3－
=－2；
（2）
．
17. 第31届世界大学生运动会于2023年7月28日至8月8日在成都举行，
某校开展了“热爱体育，喜迎大运”系列活动，增设篮球、足球、柔道、射击共四个课外活动项目．
为了解全校1800名同学对增设的四个活动项目的喜爱情况，在全校范围内随机抽取了若干名同学，
对他们喜爱的项目（每人限选一项）进行了问卷调查，将数据进行了统计，
并绘制成了如图所示的条形统计图和扇形统计图，请回答下列问题：

(1)参加问卷调查的同学共______名，补全条形统计图；
(2)估计该校1800名同学中喜爱篮球运动的人数；
(3)学校准备组建一支校足球队，某班甲、乙、丙、丁四名同学平时都很喜欢足球运动，现决定从这四人中任选两名同学加入球队，请你用树状图或列表法求恰好选中乙、丙两名同学的概率．
【答案】(1)60，补全条形统计图见详解.
(2)该校1800名同学中喜爱篮球运动的人数约为540人.
(3).
【分析】本题考查列表法与树状图法、条形统计图、扇形统计图、用样本估计总体，能够理解条形统计图和扇形统计图，熟练掌握列表法与树状图法以及用样本估计总体是解答本题的关键．
（1）用喜爱足球的人数除以其所占的百分比可得参加问卷调查的同学的人数，用参加问卷调查的同学的人数分别减去喜爱篮球、足球、射击的人数，求出喜爱柔道的人数，补全条形统计图即可．
（2）根据用样本估计总体，用1800乘以参加问卷调查的同学中喜爱篮球运动的人数的百分比，即可得出答案．
（3）画树状图得出所有等可能的结果数和恰好选中乙、丙两名同学的结果数，再利用概率公式可得出答案．
【详解】（1）解：参加问卷调查的同学共（名）
喜爱柔道的人数为（名），补全条形统计图如图所示；
（2）解：（人），
∴该校1800名同学中喜爱篮球运动的人数约为540人；
（3）画树状图如下：
由图可知，共有12种等可能结果，其中恰好选中乙、丙两名同学的结果有2种，
∴恰好选中乙、丙两名同学的概率为．
18 .近几年中学生近视的现象越来越严重，为响应国家的号召，某公司推出了如图1所示的护眼灯，
其侧面示意图（台灯底座高度忽略不计）如图2所示，其中灯柱BC＝18cm，灯臂CD＝33cm，
灯罩DE＝20cm，BC⊥AB，CD，DE分别可以绕点C，D上下调节一定的角度．经使用发现：
当∠DCB＝140°，且ED∥AB时，台灯光线最佳．求此时点D到桌面AB的距离．
（精确到0.1cm，参考数值：sin50°≈0.77，cs50°≈0.64，tan50°≈1.19）

【答案】点D到桌面AB的距离约为43.4cm
【分析】根据题意，作出合适的辅助线，然后根据锐角三角函数，即可得到DF的长，再根据FG＝CB，即可求得DG的长，从而可以解答本题．
【详解】解：过点D作DG⊥AB，垂足为G，过点C作CF⊥DG，垂足为F，如图所示，

∵CB⊥AB，FG⊥AB，CF⊥FG，
∴∠B＝∠BGF＝∠GFC＝90°，
∴四边形BCFG为矩形，
∴∠BCF＝90°，FG＝BC＝18cm，
又∵∠DCB＝140°，
∴∠DCF＝50°，
∵CD＝33cm，∠DFC＝90°，
∴DF＝CD•sin50°≈33×0.77＝25.41（cm），
∴DG≈25.41+18≈43.4（cm），
答：点D到桌面AB的距离约为43.4cm．
19 . 某药店选购A、B两种品牌的医用外科口罩，B品牌口罩每个进价比A品牌口罩每个进价多0.7元，
若用7200元购进A品牌数量是用5000元购进B品牌数量的2倍．
（1）求A、B两种品牌的口罩每个进价分别为多少元？
（2）若A品牌口罩每个售价为2元，B品牌口罩每个售价为3元，
药店老板决定一次性购进A、B两种品牌口罩共6000个，
在这批口罩全部出售后所获利润不低于1800元．则最少购进B品牌口罩多少个？
【答案】（1）1.8元；2.5元 （2）2000个
【分析】（1）设A种品牌的口罩每个进价为x元，则B品牌口罩每个进价为（x+0.7）元，根据用7200元购进A品牌数量是用5000元购进B品牌数量的2倍列出方程，解方程即可．
（2）先设B种品牌口罩购进m件，则A品牌口罩购进（6000-m）个，根据全部出售后所获利润不低于3000元列出不等式，求解即可．
【详解】（1）设A种品牌的口罩每个进价为x元，则B品牌口罩每个进价为（x+0.7）元，依题意得：
解得x=1.8，
经检验x=1.8是原方程的解，
x+1.8=2.5（元），
答：A种品牌的口罩每个的进价为1.8元，B种品牌的口罩每个的进价为2.5元．
（2）设购进B种品牌的口罩m个，则A品牌口罩购进（6000-m）个，根据题意得，
（2-1.8）（6000-m）+（3-2.5）m≥1800，
解得m≥2000，
∵m为整数，
∴m的最小值为2000．
答：最少购进种B品牌的口罩2000个．
20 . 如图，已知，是一次函数的图像和反比例函数的图像的两个交点．

(1)求反比例函数和一次函数的解析式；
(2)求的面积；
(3)根据图像直接写出不等式时的解集．
【答案】(1)
(2)6
(3)或
【分析】（1）先把代入求解反比例函数解析式，再求解A的坐标，再利用待定系数法求解一次函数的解析式即可；
（2）先求解C的坐标，再利用，从而可得答案.
（3）由可得：一次函数的图象在反比例函数图象的下方，结合函数图象可得答案.
【详解】（1）解：把代入得：

所以反比例函数的解析式为：
把代入得

把代入得：
解得：
所以一次函数的解析式为：
（2）解：为
令 则 即

（3）解：由可得：
一次函数的图象在反比例函数图象的下方，
所以：或
21 .如图，是的直径，是的切线，连接，过作交于点，
连接并延长，交延长线于．

(1)求证：是的切线；
(2)若，求的长．
【答案】(1)见解析
(2)
【分析】本题考查圆切线的判定与性质
（1）连接，利用求证即可求证即得证；
（2）通过勾股定理,再通过勾股定理即可求出的长．
【详解】（1）解：证明：如图，连接OD
∵
∴，
∵
∴
∴
在与中
∴(SAS)
∴
∵AC是切线．
∴
∴
∵点D在上，OD为半径，且
∴CE是的切线
（2）解：∵CE是的切线
∴
设半径为，在Rt中，，由勾股定理得：
∵，
∴
解得：
∵
∴
设，在Rt中，，由勾股定理得：
∴
解得：
∴CD的长为6
22. 如图，已知抛物线与一直线相交于，两点，与y轴交于点N．

(1)求抛物线的函数关系式；
(2)求直线AC的函数关系式；
(3)若P是抛物线上位于直线AC上方的一个动点．求面积的最大值．
（1）解：由抛物线y＝−x2＋bx＋c过点A（1，0），C（−2，3），得
，
解得，
故抛物线为y＝−x2−2x＋3；
（2）设直线为y＝kx＋n过点A（1，0），C（−2，3），则
，
解得，
故直线AC为y＝−x＋1；
（3）如图，过点作轴，交于点，
∵直线AC为y＝−x＋1；
设Q（x，−x＋1），则P（x，−x2−2x＋3），
∴PQ＝（−x2−2x＋3）−（−x＋1）＝−x2−x＋2，
∴S△APC＝
＝
＝，
∴△APC面积的最大值为
23. 在直角△ABC中，∠ACB=90°，AC=3，BC=4，
点D、E和F分别是斜边AB、直角边AC和直角边BC上的动点，∠EDF=90°，
(1)如图1，若四边形DECF是正方形，求这个正方形的边长．
(2)如图2，若E点正好运动到C点，并且tan∠DCF=，求BF的长．
(3)如图3，当时，求的值
【答案】(1)；
(2)1；
(3)
【分析】（1）设正方形的边长为x，则AE＝3－x，由正方形的性质，得DEBC，则AE：AC＝DE：BC，代入计算即可求解；
（2）过D点作DG⊥BC，垂足为G点，由tan∠DCF＝，得DG：CG＝1：2，设DG＝y，则CG＝2y，则BG＝4－2x，根据DGAC，得DG：AC＝BG：BC，代入即可求得x=1.2，从而求得BG＝4－2x＝1.6，再根据tan∠GDF =tan∠DCF＝，得，即可求得FG＝0.6，然后由FB＝BG－FG求解即可；
（3）过D点作DM⊥AC，垂足为M点，作DN⊥BC，垂足为N点，先由勾股定理求得AB=5，再证明Rt△DME∽Rt△DNF，得＝，由=，得=，设DM＝z，则DN＝2z，再由DMBC ，得DM：BC＝AM：AC＝AD：AB，即z：4＝（3－2z）：3 ，解得 z＝，所以：4＝AD：5 ，求得AD＝，BD＝5－＝，即可代入求解．
【详解】（1）解：∵四边形AOBC是的正方形，
∴DEBC，
∴AE：AC＝DE：BC
设正方形的边长为x，则AE＝3－x，
∴（3－x）：3＝x：4，
解得 x＝，
即这个正方形的边长为；
（2）解：过D点作DG⊥BC，垂足为G点，如图2，
∵tan∠DCF＝，
∴DG：CG＝1：2
设DG＝y，则CG＝2y，
∴BG＝4－2y，
∵DGAC，
∴DG：AC＝BG：BC，
∴y：3＝（4－2y）：4，解得 y＝1.2 ，
BG＝4－2y＝1.6，
∵∠EDF＝，
∴∠CDG＋∠GDF＝，
∵DG⊥BC，
∴∠CDG＋∠DCG＝，
∴∠GDF＝∠DCG，
∵tan∠DCF＝，
∴tan∠GDF＝，
∴，
∵DG＝1.2，
∴FG＝0.6，
∴FB＝BG－FG＝1.6－0.6 ＝1；
（3）解：过D点作DM⊥AC，垂足为M点，过D点作DN⊥BC，垂足为N点，如图3，
∵∠ACB＝，AC＝3，BC＝4，
∴AB＝5，
∵DM⊥AC，DN⊥BC，∠ACB＝，
∴∠MDN＝，
∴∠MDE＋∠EDN＝，
∵∠EDF＝，
∴∠FDN＋∠EDN＝，
∴∠MDE＝∠FDN，
∴Rt△DME∽Rt△DNF，
∴＝，
∵=，
∴=，
设DM＝z，则DN＝2z，
∵DMBC ，
∴DM：BC＝AM：AC＝AD：AB，
∴z：4＝（3－2z）：3 ，解得 z＝，
∴：4＝AD：5 ，
∴AD＝，BD＝5－＝，
∴＝．
册数
0
1
2
3
4
人数
3
13
16
17
1