



2024年浙江省杭州市九年级数学学业水平考试三轮冲刺模拟练习试卷(原卷+解析)
展开注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答填空题时,请将每小题的答案直接填写在答题卡中对应横线上。写在本试卷上无效。
4.回答解答题时,每题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),
请将解答过程书写在答题卡中对应的位置上。写在本试卷上无效。
5.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本题有10小题,每小题3分,共30分)
1 .2024的倒数是( )
A.B.2024C.D.
2.运动会的领奖台可以近似的看成如图所示的立体图形,则它的左视图是( )
A. B. C. D.
3 .神舟十五号的飞行任务是中国载人航天工程空间站建造阶段的最后一次飞行任务,
自此我国将完成空间站建造,神舟十五号距地面高度约为345000米.
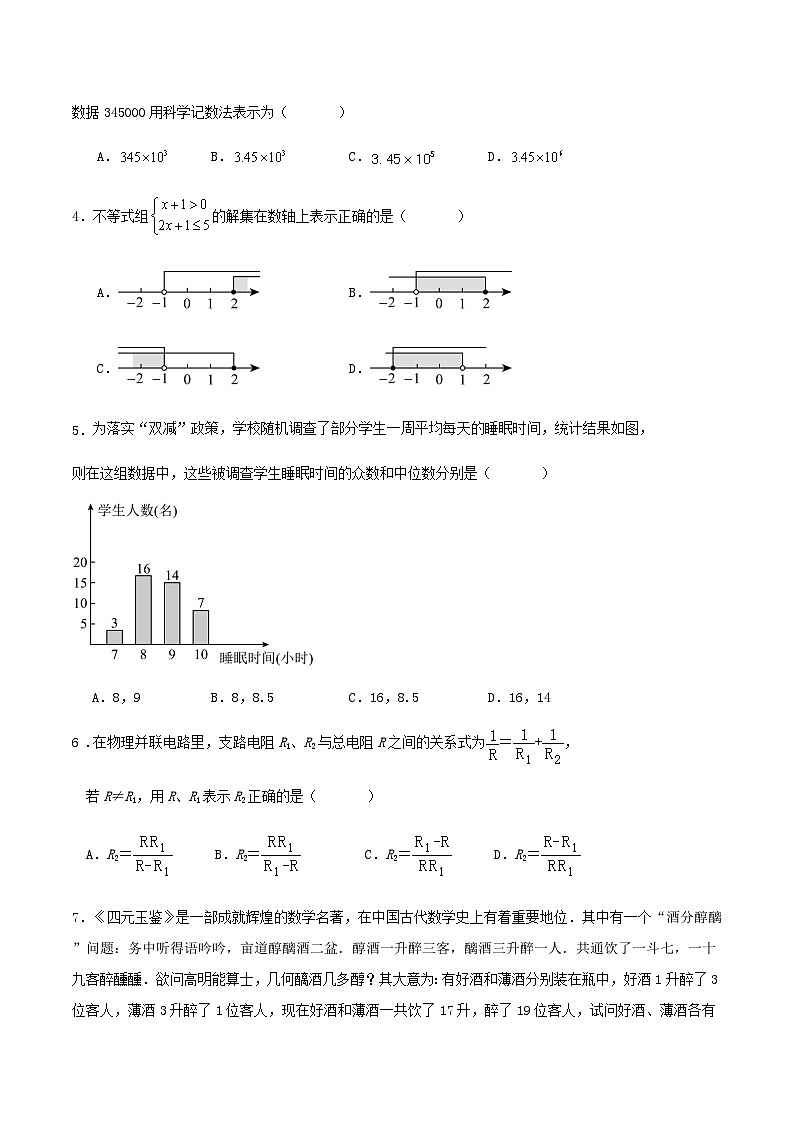
数据345000用科学记数法表示为( )
A.B.C.D.
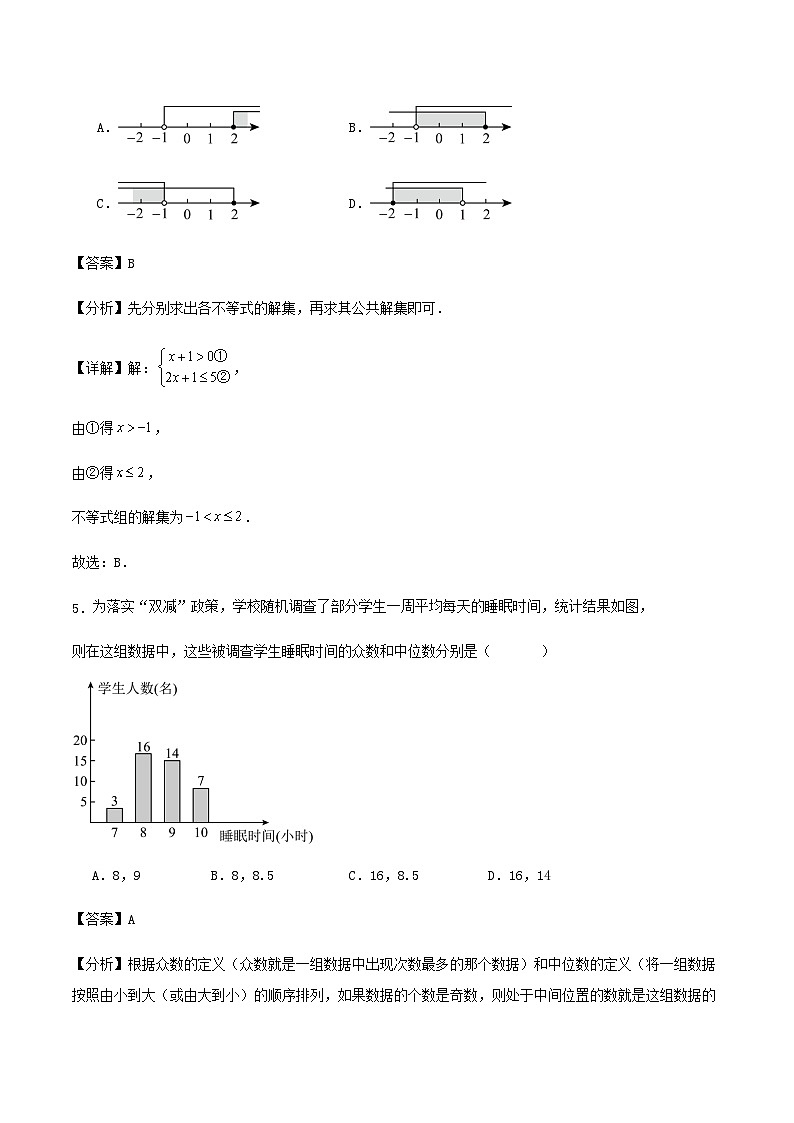
4.不等式组的解集在数轴上表示正确的是( )
A.B.
C.D.
为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如图,
则在这组数据中,这些被调查学生睡眠时间的众数和中位数分别是( )
A.8,9B.8,8.5C.16,8.5D.16,14
6 .在物理并联电路里,支路电阻R1、R2与总电阻R之间的关系式为=+,
若R≠R1,用R、R1表示R2正确的是( )
A.R2= B.R2=C.R2= D.R2=
7.《四元玉鉴》是一部成就辉煌的数学名著,在中国古代数学史上有着重要地位.其中有一个“酒分醇醨”问题:务中听得语吟吟,亩道醇醨酒二盆.醇酒一升醉三客,醨酒三升醉一人.共通饮了一斗七,一十九客醉醺醺.欲问高明能算士,几何醨酒几多醇?其大意为:有好酒和薄酒分别装在瓶中,好酒1升醉了3位客人,薄酒3升醉了1位客人,现在好酒和薄酒一共饮了17升,醉了19位客人,试问好酒、薄酒各有多少升?若设好酒有升,薄酒有升,根据题意列方程组为( )
A.B.C.D.
8 . 如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,
则∠OBC的余弦值为( )
A.B.C.D.
9.已知线段,按如下步骤作图:
①取线段中点C;
②过点C作直线l,使;
③以点C为圆心,长为半径作弧,交l于点D;
④作的平分线,交l于点E.则的值为( )
A.B.C.D.
如图,在正方形中,为中点,连结,延长至点,使得,以为边作正方形,《几何原本》中按此方法找到线段的黄金分割点.现连结并延长,分别交,于点,,若:的面积与的面积之差为,则线段的长为( )
A.B.C.D.
二、填空题(本题有6小题,每小题4分,共24分)
11. 若,且m﹣n=﹣3,则m+n= .
12.一只不透明的袋中装有2个白球和n个黑球,这些球除颜色外都相同,
搅匀后从中任意摸出1个球,摸到白球的概率为,那么黑球的个数是 .
13. 不等式组的解集为 .
14 .往直径为的圆柱形容器内装入一些水以后,截面如图,若水面宽,
则水的最大深度为 .
如图,在矩形和正方形中,点A在y轴正半轴上,点C,F均在x轴正半轴上,
点D在边上,,.若点B,E在同一个反比例函数的图象上,
则这个反比例函数的表达式是 .
16.如图,在矩形纸片ABCD中,AD=10,AB=8,将AB沿AE翻折,使点B落在处,AE为折痕;
再将EC沿EF翻折,使点C恰好落在线段EB'上的点处,EF为折痕,连接.
若CF=3,则tan= .
解答题(本题有8小题,第17-19题每题6分,第20、21题每题8分,
第22、23题每题10分,第24题12分,共66分)
17.(1)计算:.
(2)先化简,再求值:,其中x是满足条件的合适的非负整数.
18.宪法是国家的根本法,是治国安邦的总章程.学法辨是非、知法明荣辱、守法正社风、用法止纷争,弘扬并践行宪法精神是当代青少年的义务与担当.某校举行以“学宪法,讲宪法”为主题的宣传教育活动,并举办了宪法知识竞赛.据统计:所有学生的成绩均及格,竞赛成绩x分(满分100分)分为4个等级:A等级,B等级,C等级,D等级.为了解学生的成绩分布情况,教务处随机抽取了部分学生的成绩,并绘制成如图两幅不完整的统计图:
(1)本次抽取的学生共有 ___________人,他们成绩的中位数落在 ___________等级;
(2)补全频数分布直方图,扇形统计图中D等级所对应的圆心角的度数为 ___________;
(3)若竞赛成绩为优秀,估计全校1000名学生中成绩达到优秀的人数;
(4)九(1)班满分的学生为两名男生和两名女生,班主任将从中随机抽取两名学生向全校宣传宪法.请用列表或画树状图的方法求恰好抽到一名男生和一名女生的概率.
19.如图,在菱形中,于点,于点,连接
(1)求证:;
(2)若,求的度数.
20.已知:一次函数y1=x﹣2﹣k与反比例函数y2=(k≠0).
(1)若一次函数y1的图象经过点(﹣1,﹣4),
①求函数y1、y2的表达式,并求出两个函数图象的交点坐标;
②当y1<y2,写出x的取值范围.
(2)试证明:当k取任何不为0的值时,两个函数的图象总有交点.
21 .第19届亚运会于2023年9月23日至10月8日在杭州举办,吉祥物为“宸宸”、“琮琮”、“莲莲”.
如图,某校准备举行“第19届亚运会”知识竞赛活动,拟购买30套吉祥物(“宸宸”、“琮琮”、“莲莲”)
作为竞赛奖品.某商店有甲,乙两种规格,其中乙规格比甲规格每套贵20元.
(1)若用700元购买甲规格与用900元购买乙规格的数量相同,求甲、乙两种规格每套吉祥物的价格;
(2)在(1)的条件下,若购买甲规格数量不超过乙规格数量的2倍,如何购买才能使总费用最少?
随着自动化设备的普及,公园中引入了自动喷灌系统.
图1是某公园内的一个可垂直升降的草坪喷灌器,从喷水口喷出的水柱均为形状相同的抛物线,
图2是该喷灌器喷水时的截面示意图.
(1)喷水口A离地高度为,喷出的水柱在离喷水口水平距离为处达到最高,高度为,且水柱刚好落在公园围栏和地面的交界B处.
①以O为原点,以为x轴的正半轴建立平面直角坐标系,求抛物线的解析式;
②求喷灌器底端O到点B的距离;
(2)现准备在公园内沿围栏建花坛,花坛的截面示意图为矩形(如图3),其中高为.宽为.为达到给花坛喷灌的效果,需将喷水口A向上升高,使水柱经过上一点(包含两点),求h的取值范围.
在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE,点E在△ABC的内部,
连接EC,EB和ED,设EC=k•BD(k≠0).
(1)当∠ABC=∠ADE=60°时,如图1,请求出k值,并给予证明;
(2)当∠ABC=∠ADE=90°时:
①如图2,(1)中的k值是否发生变化,如无变化,请给予证明;如有变化,请求出k值并说明理由;
②如图3,当D,E,C三点共线,且E为DC中点时,请求出tan∠EAC的值.
24.如图1,为的对角线,的外接圆交于点.
(1)求证:;
(2)如图2,当时,连接、,求证;
(3)如图3,在(2)的条件下,记、的交点为点,当时,求的值.
2024年山东省青岛市九年级学业水平考试数学三轮冲刺模拟练习试卷(原卷+解析): 这是一份2024年山东省青岛市九年级学业水平考试数学三轮冲刺模拟练习试卷(原卷+解析),文件包含2024年山东省青岛市九年级学业水平考试数学三轮冲刺模拟练习试卷解析docx、2024年山东省青岛市九年级学业水平考试数学三轮冲刺模拟练习试卷docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。
2024年广东省初中学业水平考试数学三轮复习冲刺模拟练习试卷(原卷+解析): 这是一份2024年广东省初中学业水平考试数学三轮复习冲刺模拟练习试卷(原卷+解析),文件包含2024年广东省初中学业水平考试数学二模练习试卷解析docx、2024年广东省初中学业水平考试数学三轮复习冲刺模拟练习试卷docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
2024年浙江省九年级数学学业水平考试冲刺模拟练习试卷(原卷+解析): 这是一份2024年浙江省九年级数学学业水平考试冲刺模拟练习试卷(原卷+解析),文件包含2024年浙江省初中学业水平考试冲刺模拟练习试卷解析docx、2024年浙江省初中学业水平考试冲刺模拟练习试卷docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。












