最新中考数学思想方法讲与练 【新定义问题】四边形中的新定义问题

这是一份最新中考数学思想方法讲与练 【新定义问题】四边形中的新定义问题，文件包含中考数学思想方法讲与练新定义问题四边形中的新定义问题教师版docx、中考数学思想方法讲与练新定义问题四边形中的新定义问题学生版docx等2份试卷配套教学资源，其中试卷共70页， 欢迎下载使用。
一、复习方法
1.以专题复习为主。 2.重视方法思维的训练。
3.拓宽思维的广度，培养多角度、多维度思考问题的习惯。
二、复习难点
1.专题的选择要准，安排时间要合理。 2.专项复习要以题带知识。
3.在复习的过程中要兼顾基础，在此基础上适当增加变式和难度，提高能力。
四边形中的新定义问题
知识方法精讲
1．解新定义题型的方法：
方法一 :从定义知识的新情景问题入手
这种题型它要求学生在新定义的条件下，对提出的说法作出判断，主要考查学生阅读理解能力，分析问题和解决问题的能力．因此在解这类型题时就必须先认真阅读，正理解新定义的含义；再运用新定义解决问题；然后得出结论。
方法二：从数学理论应用探究问题入手
对于涉及到数学理论的题目，要解决后面提出的新问题，必须仔细研究前面的问题解法．即前面解决问题过程中用到的知识在后面问题中很可能还会用到，因此在解决新问题时，认真阅读，理解阅读材料中所告知的相关问题和内容，并注意这些新知识运用的方法步骤．
方法三：从日常生活中的实际问题入手
对于一些新定义问题，出题的方向通常借助生活问题，那么处理此类问题需要结合生活实际，再将问题转化成数学知识、或者将生活图形转化为数学图形，从而利用数学知识进行解答。
2．解新定义题型的步骤：
(1)理解“新定义”——明确“新定义”的条件、原理、方法、步骤和结论.
(2)重视“举例”,利用“举例”检验是否理解和正确运用“新定义”;归纳“举例”提供的解题方法.归纳“举例”提供的分类情况.
(3)类比新定义中的概念、原理、方法，解决题中需要解决的问题.
3．多边形
（1）多边形的概念：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形．
（2）多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线．
（3）正多边形的概念：各个角都相等，各条边都相等的多边形叫做正多边形．
（4）多边形可分为凸多边形和凹多边形，辨别凸多边形可用两种方法：①画多边形任何一边所在的直线整个多边形都在此直线的同一侧．②每个内角的度数均小于180°，通常所说的多边形指凸多边形．
（5）重心的定义：平面图形中，多边形的重心是当支撑或悬挂时图形能在水平面处于平稳状态，此时的支撑点或者悬挂点叫做平衡点，或重心．
常见图形的重心（1）线段：中点（2）平行四边形：对角线的交点（3）三角形：三边中线的交点（4）任意多边形．
日期：2022/2/3 18:26:37；用户：13632669984；邮箱：13632669984；学
一．填空题（共3小题）
1．（2021•梓潼县模拟）新定义：有一组对角互余的凸四边形称为对余四边形，如图，已知在对余四边形中，，，，，那么边的长为 9 ．
【考点】解直角三角形
【分析】如图，过点作于，过点作于，连接．解直角三角形求出，即可解决问题
【解答】解：如图，过点作于，过点作于，连接．
在中，，
可以假设，，则，
，
，，
，
，
，
，，
，
在中，，
，
，，
，
．
故答案为：9．
【点评】本题考查解直角三角形，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．
2．（2020秋•武汉期中）定义：有一组对角互余的四边形叫做对余四边形，如图，在对余四边形中，，，，，则线段 ．
【考点】全等三角形的判定与性质；勾股定理；旋转的性质
【分析】对余四边形的定义得出，将绕点逆时针旋转，得到，连接，则，，得出，，，则是等边三角形，得出，易证，由，得出，则，由勾股定理即可得出结果．
【解答】解：对余四边形中，，
，
，
将绕点逆时针旋转，得到，连接，如图所示，
，
，，，
是等边三角形，
，
，
，
，
，
，
，
，
，
，
，
，
，
故答案为：．
【点评】本题考查了对余四边形的定义、旋转的性质、等边三角形的判定与性质、三角形内角和定理、勾股定理等知识；熟练掌握对余四边形的定义和旋转的性质是解题的关键．
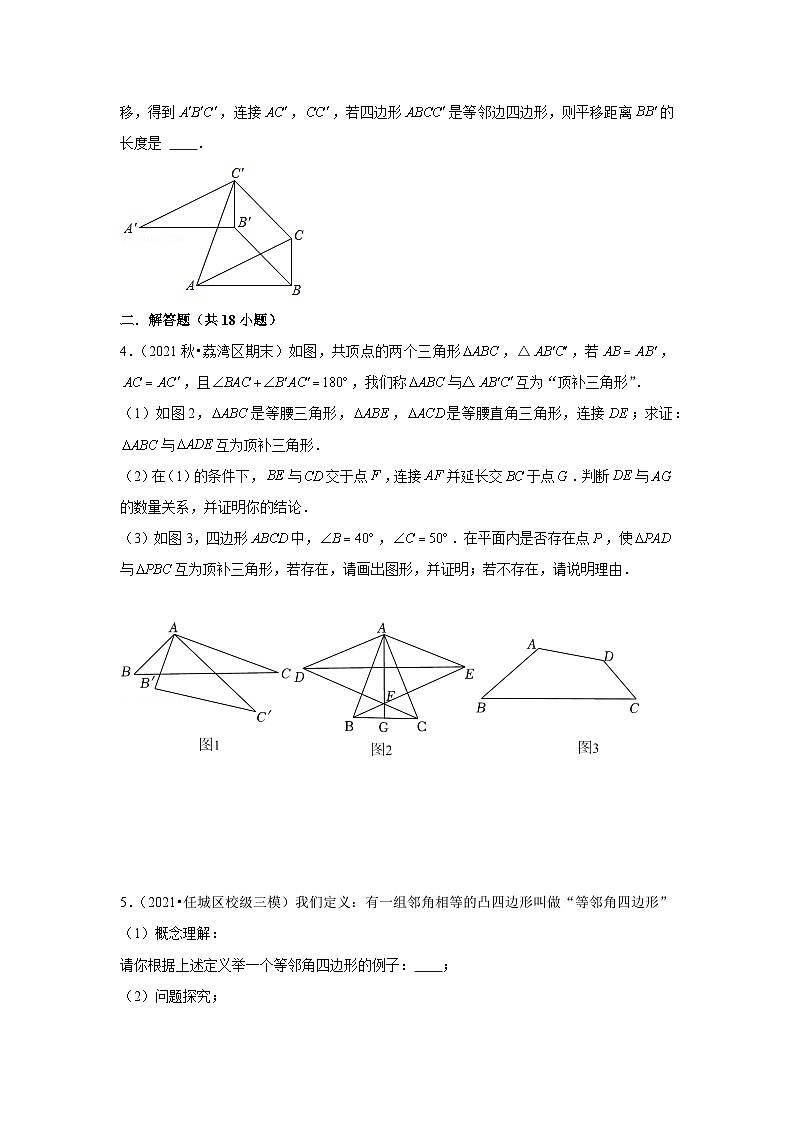
3．（2020•奉化区校级模拟）定义：有一组邻边相等的凸四边形叫做等邻边四边形．如图，在中，，，，将沿的平分线的方向平移，得到，连接，，若四边形是等邻边四边形，则平移距离的长度是 1或 ．
【考点】勾股定理；平移的性质
【分析】由平移的性质得到，，，，，①如图，当时，；②如图，当时，③如图2，当时，则，延长交于，设，根据勾股定理即可得到结论．
【解答】解：将平移得到△，
，，，，，
①如图1，当时，；
②如图1，当时，
，是的角平分线，
，
延长交于，
，，
，
，
设，
，，，
，
，
整理方程为：，
△，
此方程无实数根，故这种情况不存在；
③如图2，当时，则，
延长交于，
，，
，
，
设，
，，，
，
，
解得：，
，
综上所述，若四边形是等邻边四边形，则平移距离的长度是1或，
故答案为：1或．
【点评】此题主要考查勾股定理，平移的性质，理解“等邻边四边形”的定义是解本题的关键．
二．解答题（共18小题）
4．（2021秋•荔湾区期末）如图，共顶点的两个三角形，△，若，，且，我们称与△互为“顶补三角形”．
（1）如图2，是等腰三角形，，是等腰直角三角形，连接；求证：与互为顶补三角形．
（2）在（1）的条件下，与交于点，连接并延长交于点．判断与的数量关系，并证明你的结论．
（3）如图3，四边形中，，．在平面内是否存在点，使与互为顶补三角形，若存在，请画出图形，并证明；若不存在，请说明理由．
【考点】三角形综合题
【分析】（1）等腰三角形的性质和等腰直角三角形的性质可得，，可证，可得结论；
（2）先证是的垂直平分线，再由“”可证，可得，即可得结论；
（3）延长交延长线于点，作的垂直平分线交的垂直平分线于点，连接，，，，由线段垂直平分线的性质可得，，，，由等腰三角形的性质可得，，可证，即可证与互为“顶补三角形”．
【解答】（1）证明：是等腰三角形，，是等腰直角三角形，
，，
，
，
与互为顶补三角形；
（2），理由如下：
如图2，设与的交点为，与交于点，与交于点，
是等腰三角形，，是等腰直角三角形，
，，，
，
，，，
，
，
，
又，，
，
，
又，
是的垂直平分线，
又，
，
，
又，
，，
，
，
，
又，，
，
，
．
（3）证明：如图，延长交延长线于点，作的垂直平分线交的垂直平分线于点，连接，，，，
垂直平分，垂直平分，
，，，，
，，
，
，
又，，
，
，
，
，且，，
与互为“顶补三角形”．
【点评】本题是三角形综合题，考查了等腰三角形的性质，直角三角形的性质，全等三角形的判定和性质等知识，灵活运用这些性质解决问题是本题的关键．
5．（2021•任城区校级三模）我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”
（1）概念理解：
请你根据上述定义举一个等邻角四边形的例子： 矩形或正方形 ；
（2）问题探究；
如图1，在等邻角四边形中，，，的中垂线恰好交于边上一点，连结，，试探究与的数量关系，并说明理由；
（3）应用拓展；
如图2，在与中，，，，将绕着点顺时针旋转角得到△（如图，当凸四边形为等邻角四边形时，求出它的面积．
【考点】四边形综合题
【分析】（1）矩形或正方形邻角相等，满足“等邻角四边形”条件；
（2）结论：，证明；
（3）分两种情况考虑：Ⅰ、当时，延长，交于点，如图1，由，求出四边形面积；
Ⅱ、当时，过点作于点，如图2，由，求出四边形面积即可．
【解答】解：（1）矩形或正方形是一个等邻角四边形．
故答案为：矩形，正方形；
（2）结论：，
理由：连接，，如图1所示：
是的垂直平分线，是的垂直平分线，
，，
，，
，，即，
，
，
；
（3）分两种情况考虑：
当时，延长，交于点，
如图所示，
，
，
设，
由勾股定理得：，
解得：，
过点作于，
，
△，
，即，
解得：，
；，
则；
当时，过点作于点，
如图所示，
四边形是矩形，
，
在中，根据勾股定理得：，
，，
则．
【点评】此题是四边形综合题，主要考查了“等邻角四边形”的理解，三角形，四边形的内角和定理，角平分线的意义，勾股定理，旋转的性质，相似三角形的性质和判定，理解“等邻角四边形”的定义是解本题的关键，分类讨论是解本题的难点，是一道中考常考题．
6．（2020秋•崇川区期末）定义：三角形中，连接一个顶点和它所对的边上一点，如果所得线段把三角形的周长分成相等的两部分，则称这条线段为三角形的“周长平分线”．
（1）下列与等腰三角形相关的线段中，一定是所在等腰三角形的“周长平分线”的是 ② （只要填序号）；
①腰上的高；②底边上的中线；③底角平分线．
（2）如图1，在四边形中，，为的中点，．取中点，连接．求证：是的“周长平分线”．
（3）在（2）的基础上，分别取，的中点，，如图2．请在上找点，，使为的“周长平分线”， 为的“周长平分线”．
①用无刻度直尺确定点，的位置（保留画图痕迹）；
②若，，直接写出的长．
【考点】四边形综合题
【分析】（1）由等腰三角形的底边上的中线平分底边可求解；
（2）由等腰直角三角形的性质可得，，，由“”可证，可得，可得结论；
（3）①由是的中垂线，是的中垂线可求解；
②如图2，过点作于，过点作于，连接，，由“”可证，可得，，由勾股定理可求，的长，即可求解．
【解答】（1）解：一定是所在等腰三角形的“周长平分线”的是底边上的中线，
故答案为：②；
（2）证明：如图1，延长，交于点，连接，
，
，，
为的中点，
，，，
，
，
，
，
点是的中点，
，
，
是的“周长平分线”；
（3）①如图2，连接并延长交于点，连接并延长交于点，则点，点为所求，
②如图2，过点作于，过点作于，连接，，
，
，，
，，
，，
，，
，
，
，
又，，
，
，，
，，点是的中点，
，，
点，点分别是，的中点，
是的中垂线，是的中垂线，
，，
，
，
，
同理可求，
．
【点评】本题是四边形综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质，勾股定理等知识，理解三角形的“周长平分线”的定义并运用是解题的关键．
7．（2021秋•诸暨市期中）【了解概念】
在凸四边形中（内角度数都小于，若一边与它的两条邻边组成的两个内角相等，则称该四边形为邻等四边形，这条边叫做这个四边形的邻等边．
【理解应用】
（1）邻等四边形中，，，则的度数 130 ；
（2）如图，四边形为邻等四边形，为邻等边，且，求证：；
【拓展提升】
（3）在平面直角坐标系中，为邻等四边形的邻等边，且边与轴重合，已知，，，若在边上使的点有且只有1个，求的值．
【考点】相似形综合题
【分析】（1）分三种情况考虑：①由为邻等边，②由为邻等边，③由为邻等边，根据邻等四边形的定义即可求解；
（2）根据相似三角形的判定解答即可；
（3）分两种情况：①若点在点右侧，如图1，过点作轴于点，过点作轴于点，由为邻等边，则有，可证，可得，设点，由三角函数可求，可求、横坐标之差为2，，将，，，，代入得：，由于在边上使的点有且只有1个，即上述方程有且只有1个实数根，运用根的判别式即可求得答案；
②若点在点左侧，如图2，过点作轴于点，过点作轴于点，根据，可得，同①方法即可求得答案．
【解答】解：（1）①若为邻等边，则，
不为凸四边形，所以舍去；
②若为邻等边，则，
（舍；
③若为邻等边，则，
，
．
故答案为：130；
（2）证明：四边形为邻等四边形，为邻等边，
，
，
，
，，
，
；
（3）①若点在点右侧，如图1，过点作轴于点，过点作轴于点，
为邻等边，
，
，
，
，，
，
，
，
设点，
，，
，
，，
，
，
，
，
由（2）知，，
，
，
，
，，
，，
，
，
，
在边上使的点有且只有1个，即上述方程有且只有1个实数根，
△，
，
点在点右侧，
；
②若点在点左侧，如图2，过点作轴于点，过点作轴于点，
，，
，
，
，，
，
，
，
由①得：，，，
，，，，
，
，
在边上使的点有且只有1个，即上述方程有且只有1个实数根，
△，
，
点在点左侧，
；
综上所述，．
【点评】本题是相似综合题，考查新定义图形，仔细阅读题目，抓住定义中的性质，会验证新定义图形，相似三角形的判定与性质，锐角三角函数，一元二次方程根的判别式，利用相似三角形的性质构造关于的一元二次方程是解题关键．
8．（2021秋•驻马店期中）定义：有一组邻边垂直且对角线相等的四边形为垂等四边形．
（1）矩形 是 垂等四边形（填“是”或“不是” ；
（2）如图1，在正方形中，点，，分别在，，边上．若四边形是垂等四边形，且，，求证：；
（3）如图2，在中，，，，以为对角线，作垂等四边形，过点作的延长线的垂线，垂足为，且与相似，求四边形的面积．
【考点】相似形综合题
【分析】（1）根据“垂等四边形”的定义进行分析；
（2）通过的性质推知；然后根据四边形是垂等四边形的性质知；最后由等量代换证得结论；
（3）如图2，过点作，垂足为，构造矩形．在中，利用勾股定理求得，．再由垂等四边形四边形的性质知．
分两种情况：当时，利用相似三角形的对应边成比例和勾股定理求得相关线段的长度，由求得结果；
当时，利用相似三角形的对应边成比例和勾股定理求得相关线段的长度，由求得结果．
【解答】（1）解：矩形有一组邻边垂直且对角线相等，故矩形是垂等四边形．
故答案为：是；
（2）证明：四边形为正方形，
，．
又，
，
．
四边形是垂等四边形，
，
；
（3）解：如图2，过点作，垂足为，
四边形为矩形．
，
．
在中，，
根据勾股定理得，，即，
，．
四边形为垂等四边形，
．
第一种情况：
当时，，
设，则，
．
在中，根据勾股定理得，，
即，
解得，（舍去），
，，
；
第二种情况：
当时，，
设，则，
．
在中，根据勾股定理得，，
即，
解得，（舍去），
，，
．
综上所述，四边形的面积为或．
故答案为：或．
【点评】本题主要考查了相似综合题，综合运用相似三角形的判定与性质，等腰直角三角形的判定与性质，勾股定理的应用等知识点解题，解题的关键是掌握“垂等四边形”的定义，另外解题过程中，注意方程思想的应用．难度较大．
9．（2021秋•市北区期中）阅读理解：
如图1，在四边形的边上任取一点（点不与点、点重合），分别连接，，可以把四边形分成三个三角形，如果其中有两个三角形相似，我们就把叫做四边形的边上的相似点；如果这三个三角形都相似，我们就把叫做四边形的边上的强相似点．
解决问题：
（1）如图1，，试判断点是否是四边形的边上的相似点，并说明理由；
（2）如图2，在矩形中，，，，，，四点均在正方形网格（网格中每个最小正方形的边长为的格点（即每个最小正方形的顶点）上，若图2中，矩形的边上存在强相似点，则 或 ；
拓展探究：
（3）如图3，将矩形沿折叠，使点落在边上的点处．若点恰好是四边形的边上的一个强相似点，试探究和的数量关系．
【考点】相似形综合题
【分析】（1）利用三角形外角的性质可得，则可证明；
（2）根据强相似点的定义，可找出符合条件的点，即可得出答案；
（3）由题意知，则，可说明点为的中点，从而解决问题．
【解答】解：（1）是，理由如下：
，，
，
又，
，
点是否是四边形的边上的相似点；
（2）如图，
故或．
故答案为：或；
（3）点恰好是四边形的边上的一个强相似点，
，
，
，
，
，
即．
【点评】本题是四边形中的新定义题，主要考查了对新定义的理解，相似三角形的判定与性质等知识，读懂题意，熟悉基本模型是解题的关键．
10．（2021秋•苏家屯区期中）我们定义对角线互相垂直的四边形叫做垂美四边形．
如图点是四边形内一点，已知，，，对角线与交于点，与交于点，与交于点．
（1）求证：四边形是垂美四边形；
（2）猜想四边形两组对边、与、之间的数量关系并说明理由；
（3）若，，，则的长为 ．
【考点】四边形综合题
【分析】（1）先，得，根据三角形内角和定理可得，最后根据垂美四边形的定义可得结论；
（2）根据勾股定理解答即可；
（3）根据等腰直角三角形和勾股定理可得和的长，代入（2）中的结论可得的长．
【解答】（1）证明：，
，
即，
，，
，
，
，
，
，
四边形是垂美四边形；
（2）解：猜想：；理由如下：
，
，
由勾股定理得，，
，
；
（3）和是等腰直角三角形，且，，
，，
，
，
．
故答案为：．
【点评】本题是四边形综合题，考查的是全等三角形的判定和性质，等腰三角形的性质，勾股定理的应用，正确理解垂美四边形的定义、灵活运用勾股定理是解题的关键．
11．我们学过了特殊的四边形，体验了通过作平行线、垂线、延长线等常用方法，把四边形问题转化为三角形问题的重要思想．除了我们学过的特殊四边形，还有很多特殊四边形．我们定义：四边形中，除一边以外其余的部分都在这条边的同侧，这个四边形就叫做凸四边形；有一组邻角相等的凸四边形就叫做“等邻角四边形”，根据这个定义，请解决下列问题．
（1）概念理解
如图（1），在中，于，点、、分别是、、的中点，连接、、、、，写一个图形中的“等邻角四边形”： 四边形 （不再添加除图形以外的字母）；
（2）解决问题
如图（2），四边形是“等邻角四边形”，且，延长、交于点．
求证：；
（3）探索研究
如图（3），中，，，，，点是边上的一个动点，当四边形成为“等邻角四边形”时，求四边形的面积．
【考点】相似形综合题
【分析】（1）根据三角形中位线定理得，所以，由直角三角形斜边上的中线等于斜边的一半可知，所以，得到，进一步推理即可得到四边形为“等邻角四边形”；
（2）过点作交于点，可证，，得，进一步变形即可得出结论；
（3）分三种情况考虑：①，四边形为直角梯形，根据梯形面积公式求出即可，②时，，求出和即可，③时，，求出和即可．
【解答】（1）解：点、分别是、的中点，
是的中位线，
，
，
于，点是的中点，
，
，
，
，
，
四边形为凸四边形，
四边形为“等邻角四边形”，
故答案为：四边形；
（2）证明：过点作交于点，
，
，
，
，
，
，
，
，
；
（3）解：分三种情：
①当时，如图：
，，
，
，
，，，
，
，
，
，
②当时，如图：
过点作于点，
，
，
，
，
中，，，，，
，
，
，
，
，
，
，
③当时，如图：
过点作交于点，过点作于点，过点作于点，过点作于点，过点作于点，
，
，
，
，
，，
，
，
，
，
，
，
，
，
，
，
，
，即，
，
，
，
，，
，即，
，
，
综上所述，四边形的面积为．
【点评】本题是相似综合题，理解新定义的条件，正确作出辅助线，找到相似三角形是解决问题的关键，分类讨论是难点．
12．（2021•鄞州区模拟）定义：有一组邻边垂直且对角线相等的四边形称为垂等四边形．
（1）写出一个已学的特殊平行四边形中是垂等四边形的是 矩形 ；
（2）如图1，在正方形中，点，，分别在，，上，四边形是垂等四边形，且，．
①求证：；
②若，求的值；
（3）如图2，在中，，，以为对角线，作垂等四边形．过点作的延长线的垂线，垂足为，且与相似，求四边形的面积．
【考点】相似形综合题
【分析】（1）根据“垂等四边形”的定义进行分析；
（2）①通过的性质推知；然后根据四边形是垂等四边形的性质知；最后由等量代换证得结论；
②如图1，过点作，垂足为，首先证明为等腰直角三角形，则；然后证得为等腰直角三角形；再次，根据等腰直角三角形的性质和已知条件得到：，．代入求值即可；
（3）解：如图2，过点作，垂足为，构造矩形．在中，利用勾股定理求得，．再由垂等四边形四边形的性质知．
分两种情况：当时，利用相似三角形的对应边成比例和勾股定理求得相关线段的长度，由求得结果；
当时，利用相似三角形的对应边成比例和勾股定理求得相关线段的长度，由求得结果．
【解答】（1）解：矩形有一组邻边垂直且对角线相等，故矩形的垂等四边形．
故答案是：矩形；
（2）①证明：四边形为正方形，
，．
又，
，
．
四边形是垂等四边形，
，
．
②解：如图1，过点作，垂足为，
四边形为矩形，
．
由①知，
．
由题意知，，，
，
即，
为等腰直角三角形，
．
又，
，
为等腰直角三角形，
，
，
，．
，
．
（3）解：如图2，过点作，垂足为，
四边形为矩形．
，
．
在中，，
根据勾股定理得，，即，
，．
四边形为垂等四边形，
．
第一种情况：
当时，，
设，则，
．
在中，根据勾股定理得，，
即，
解得，（舍去），
，，
；
第二种情况：
当时，，
设，则，
．
在中，根据勾股定理得，，
即，
解得，（舍去），
，，
．
综上所述，四边形的面积为或．
【点评】本题主要考查了相似综合题，综合运用相似三角形的判定与性质，等腰直角三角形的判定与性质，勾股定理的应用等知识点解题，解题的关键是掌握“垂等四边形”的定义，另外解题过程中，注意方程思想的应用．难度较大．
13．（2021秋•鄞州区月考）新定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．
（1）已知：如图1，四边形是“等对角四边形”， ，，，求，的度数
（2）在探究“等对角四边形”性质时：小红画了一个“等对角四边形” （如图，其中，，此时她发现成立．请你证明此结论
（3）已知：在“等对角四边形中，，，，．求对角线的长．
【考点】四边形综合题
【分析】（1）根据四边形是“等对角四边形”得出，根据四边形内角和定理求出即可；
（2）连接，根据等边对等角得出，求出，根据等腰三角形的判定得出即可；
（3）分两种情况：
①当时，延长，相交于点，先用含角的直角三角形的性质求出，得出，再用三角函数求出，由勾股定理求出；
②当时，过点作于点，于点，则，四边形是矩形，先求出、，再由矩形的性质得出，，求出、，根据勾股定理求出即可．
【解答】（1）解：四边形是“等对角四边形”， ，，，
，
；
（2）证明：如图2，连接，
，
，
，
，
，
；
（3）解：分两种情况：
①当时，延长，相交于点，如图3所示：
，，，，
，
，
，
，，
，
；
②当时，
过点作于点，于点，如图4所示：
则，四边形是矩形，
，，，
，
，
，
，
四边形是矩形，
，，
，
，
，
．
综上所述：的长为或．
【点评】本题是四边形综合题目，考查了新定义、四边形内角和定理、等腰三角形的判定与性质、勾股定理、三角函数、矩形的判定与性质等知识；本题难度较大，综合性强，特别是（3）中，需要进行分类讨论，通过作辅助线运用三角函数和勾股定理才能得出结果．
14．（2021•新吴区二模）定义：长宽比为为正整数）的矩形称为矩形．下面，我们通过折叠的方式折出一个矩形，如图所示．
操作1：将正方形沿过点的直线折叠，使折叠后的点落在对角线上的点处，折痕为．
操作2：将沿过点的直线折叠，使点、点分别落在边，上，折痕为．则四边形为矩形．
（1）证明：四边形为矩形；
（2）点是边上一动点．
①如图，是对角线的中点，若点在边上，，连接．求的值；
②若，点在边上，当的周长最小时，求的值；
③连接，作，垂足为．若，则的最小值 2 ．
【考点】相似形综合题
【分析】（1）先判断出，进而判断出四边形是矩形，再求出的值，即可得出结论；
（2）①如图，先判断出四边形是矩形，进而得出，，再判断出，进而判断出．，即可得出结论；
②作关于直线对称的点，则的周长最小，判断出，得出．进而得出．即可得出结论；
③先求出，再判断出点是为直径的圆上，即可得出结论．
【解答】证明：（1）设正方形的边长为，
是正方形的对角线，
，
由折叠性质可知，，
则四边形为矩形，
是等腰直角三角形．
，
．
四边形为矩形；
（2）①解：如图，作，，垂足分别为，．
四边形是矩形，，
四边形是矩形．
，，．
，．
为中点，
，．
，
．
．
．
．
②解：如图，作关于直线对称的点，连接交于点，连接．
则的周长最小，
，
，
设，则．
．
，
③如备用图，
四边形为矩形，，
，
，
点在以为直径的圆上，记的中点为，
，
最小
故答案为：2
【点评】此题相似形综合题，主要考查了新定义，相似三角形的判定和性质，勾股定理，矩形的性质和判定，利用对称性和垂线段最短确定出最小值是解本题的关键．
15．（2020•柯城区校级一模）【定义】若四边形的一条对角线能将四边形分割成两个相似的直角三角形，那么我们将这种四边形叫孪生分割四边形，这条对角线叫这个四边形的孪生割线．
【理解】（1）如图①，已知在正方形网格中，请在网格中找到一个格点（网格线的交点即为格点），使以，，，为顶点的四边形为孪生分割四边形．
（2）若在四边形中，，为孪生割线，若，求的长．
（3）如图②，在四边形中，，，为上一点．若四边形，均为孪生分割四边形，求．
【考点】相似形综合题
【分析】（1）根据“孪生分割四边形”的定义即可找出符合题意的点；
（2）分两种情况：①当时，如图②，过点作交的延长线于，利用三角函数求得，，再证明四边形是矩形，可得出，，进而求得，再运用勾股定理即可；②当时，如图③，过点作交的延长线于，运用三角函数求出、、，再运用勾股定理即可；
（3）分两种情况：①当时，如图④，利用平行线性质和判定求得：，再运用三角函数即可；②当时，如图⑤，过点于，可得出：，，，再运用角平分线性质即可．
【解答】解：（1）如图①，点、、即为所求的格点；
（2）四边形中，，为孪生割线，，
与相似，
①当时，如图②，过点作交的延长线于，
，，
，
，
，
四边形是矩形，
，，
，
；
②当时，如图③，过点作交的延长线于，
，，
，，
，，
，
，，
，
；
综上所述，的长为或．
（3）①当时，如图④，
，
，
，
，
，
，
，
，
，
；
②当时，如图⑤，过点于，
，，，
，，，
，
同理，，
，
；
综上所述，或1．
【点评】本题考查了相似三角形的判定和性质，平行线的判定和性质，三角函数定义，勾股定理，新定义“孪生分割四边形”等，理解并应用新定义，运用数形结合思想和分类讨论思想思考解决问题是解题关键．
16．（2020秋•安徽月考）定义：我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”．
理解：
（1）如图1，的三个顶点均在正方形网格中的格点上，若四边形是以为“相似对角线”的四边形，请用无刻度的直尺在网格中画出点（保留画图痕迹，找出3个即可）；
（2）①如图2，在四边形中，，，对角线平分．请问是四边形的“相似对角线”吗？请说明理由；
②若，求的值．
运用：
（3）如图3，已知是四边形的“相似对角线”， ．连接，若的面积为，求的长．
【考点】相似形综合题
【分析】（1）先求出，，，再分情况求出或，即可画出图形；
（2）先判断出，即可得出结论；
（3）先判断出，得出，再判断出，继而求出，即可得出结论．
【解答】解：（1）如图1所示．，，，，
四边形是以为“相似对角线”的四边形，
①当时，或，
，
，
或，
同理：当时，或，
如图中，，，，即为所求；
（2）①如图2，是四边形的“相似对角线”，
理由如下：
，平分，
，
，
，
，
，
是四边形的“相似对角线”；
②，
，
，
又，
；
（3）如图3，
是四边形的“相似对角线”，
与相似．
又，
，
，
，
过点作垂足为，
可得，
，
，
，
，
．
【点评】本题是四边形综合题，主要考查了相似三角形的判定和性质，理解新定义，锐角三角函数，判断两三角形相似是解本题的关键．
17．（2020春•开福区校级月考）定义：我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”．
（1）如图1，已知四边形在正方形网格中，顶点都在格点上，判断：四边形 是 （填“是”或“不是” 以为“相似对角线”的四边形；
（2）如图2，在四边形中，，，对角线平分．求证：是四边形的“相似对角线”；
（3）如图3，已知是四边形的“相似对角线”， ．连接，若的面积为，求的长．
【考点】相似形综合题
【分析】（1）根据勾股定理和相似三角形的判定定理即可得到结论；
（2）先判断出，即可得出结论；
（3）先判断出，得出，再判断出，继而求出，即可得出结论．
【解答】解：（1）由图1知，，，，，，，
，，，
，
，
四边形是以为“相似对角线”的四边形；
故答案为：是；
（2）证明：如图2中，
，平分，
，
，
，
，
，
是四边形的“相似对角线”；
（3）如图3，
是四边形的“相似对角线”，
与相似，
，
，
，
，
过点作于，
，
，
，
，
，
．
【点评】本题是四边形综合题，主要考查了相似三角形的判定和性质，理解新定义，锐角三角函数，判断两三角形相似是解本题的关键．
18．（2020秋•思明区校级期末）定义：有一组邻边相等的凸四边形叫做“等邻边四边形”，回答下列问题．
（1）如图1，四边形中，，，，，判断四边形是不是“等邻边四边形”，并说明理由；
（2）如图2，中，，，，现将沿的平分线方向平移得到△，连接，，若平移后的四边形是“等邻边四边形”，求的长．
【考点】几何变换综合题
【分析】（1）根据等腰三角形的性质求出，根据勾股定理求出，根据“等邻边四边形”的定义解答即可；
（2）延长交于点，根据平移的性质得到，设，根据勾股定理列出方程，解方程求出，根据等腰直角三角形的性质计算，得到答案．
【解答】解：（1）四边形是“等邻边四边形”，
理由如下：，，
，
在中，，
，
四边形是“等邻边四边形”；
（2）如图2，延长交于点，
△由平移得到，
，，，
，
平分，
，
，
设，
，
，
中，，
整理得：，
，
，（舍去），
，
．
【点评】本题考查的是平移的性质、“等邻边四边形”的定义，掌握“等邻边四边形”的定义是解题的关键．
19．（2020春•赫山区期末）阅读与探究
我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．
请结合上述阅读材料，解决下列问题：
（1）在我们所学过的特殊四边形中，是勾股四边形的是 矩形 ；（写出一种即可）
（2）下面图1，图2均为的正方形网格，点，，均在格点上，请在图中标出格点，并连接，，使得四边形符合下列要求：图1中的四边形是勾股四边形，并且是中心对称图形；图2中的四边形是勾股四边形且对角线相等，但不是中心对称图形．
【考点】多边形；作图—应用与设计作图；中心对称图形
【分析】（1）根据勾股四边形的定义判断即可．
（2）根据要求结合数形结合的思想画出图形即可．
【解答】解：（1）矩形是勾股四边形．
故答案为：矩形．
（2）如图1中，四边形即为所求．
如图2中，四边形即为所求．
【点评】本题考查作图应用与设计，中心对称图形等知识，解题的关键是理解题意．灵活运用所学知识解决问题，属于中考常考题型．
20．（2020春•奉化区期末）定义：有一组邻边垂直且对角线相等的四边形为垂等四边形．
（1）写出一个已学的特殊平行四边形中是垂等四边形的是 正方形，矩形 ．
（2）如图1，在方格纸中，，，在格点上，请画出两个符合条件的不全等的垂等四边形，使，是对角线，点在格点上．
（3）如图2，在正方形中，点，，分别在，，上，且，求证：四边形是垂等四边形．
（4）如图3，已知，，，，以为边在的右上方作等腰三角形，使四边形是垂等四边形，请直接写出四边形的面积．
【考点】几何变换综合题
【分析】（1）根据垂等四边形的定义判断即可．
（2）根据垂等四边形的定义画出图形即可．
（3）想办法证明，即可．
（4）分三种情形：①如图中，当时，连接，过点作于．②如图中，当时，连接，过点作交的延长线于，于．③如图中，当时，取的中点，连接，，过点作交的延长线于．分别求解即可．
【解答】解：（1）正方形，矩形是垂等四边形．
故答案为正方形，矩形．
（2）如图1中，四边形即为所求．
（3）在正方形中，
，，
，
，，
，
，，，
，
，
，
，
，
，
，
，
四边形是垂等四边形．
（4）①如图中，当时，连接，过点作于．
，，，
，，
四边形是垂等四边形，
，
，，
，
．
②如图中，当时，连接，过点作交的延长线于，于．
同法可得，．
③如图中，当时，取的中点，连接，，过点作交的延长线于．
设，
，
，
，，
，
，
，
，，
在中，，
，
解得，
．
【点评】本题属于几何变换综合题，考查了垂等四边形的定义，解直角三角形，等腰三角形的判定和性质等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考压轴题．
21．（2020•武昌区模拟）定义：顶点都在网格点上的四边形叫做格点四边形，端点都在网格点上的线段叫做格点线．如图1，在正方形网格中，格点线、将格点四边形分割成三个彼此相似的三角形．请你在图2、图3中分别画出格点线，将阴影四边形分割成三个彼此相似的三角形．
【考点】作图相似变换
【分析】图2中，连接、，得，相似比为；图3中，，相似比为．
【解答】解：如图所示
【点评】本题主要考查作图相似变换，解题的关键是掌握相似三角形的判定与性质及勾股定理．