
2024年初中数学学业水平考试全真模拟三(含答案)
展开一、 单选题 (本题共计8小题,总分24分)
1.(3分)下列各数中,是无理数的是( )
A.-2B.-1C.−8D.−13
2.(3分)下列图形中,是中心对称图形的是( )
A. B.
C.D.
3.(3分)如图,已知AB//CD,EF分别交AB、CD于点F、E,EG平分∠DEF,若∠1=70°,则∠DEG的度数为( )
A.55°B.50°C.45°D.40°
4.(3分)化简m2−n2m2÷m−nm的结果是( )
A.mm−nB.mm+nC.m−nmD.m+nm
5.(3分)如图,在ΔABC中,点D是BC上一点,连接AD,已知AB=5,∠B=70°,∠C=35°,若∠BAD=40°,则CD的长为( )
A.4B.5C.6D.7
6.(3分)一次函数y=−2x+1的图象向左平移b个单位长度后,恰好经过点A(−2,−1),则b的值为( )
A.3B.4C.2D.1
7.(3分)如图,AB是⨀O的直径,点C是⨀O上一点,D为BC^上一点,连接CD并延长交AB的延长线于点E,若D是CE的中点,∠CAB=45°,则∠DAE的度数为( )
A.10°B.12°C.15°D.20°
8.(3分)如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=1,下列结论:①abc<0;②a+2b=0;③3b+2c<0;④点(x1,y1),(x2,y2)在二次函数图象上,若x1
二、 填空题 (本题共计5小题,总分15分)
9.(3分)将实数−π,0,−5和2由小到大用“<”号连接起来为_________.
10.(3分)每天供给地球光和热的太阳与我们的距离非常遥远,它与地球的距离约为150000000千米,将数据150000000用科学记数法表示为___________.
11.(3分)如图,点E、F分别是正方形ABCD的边BC、CD上一点,连接AE、EF、AF,若AE=AF,则∠CFE的度数为_____________.
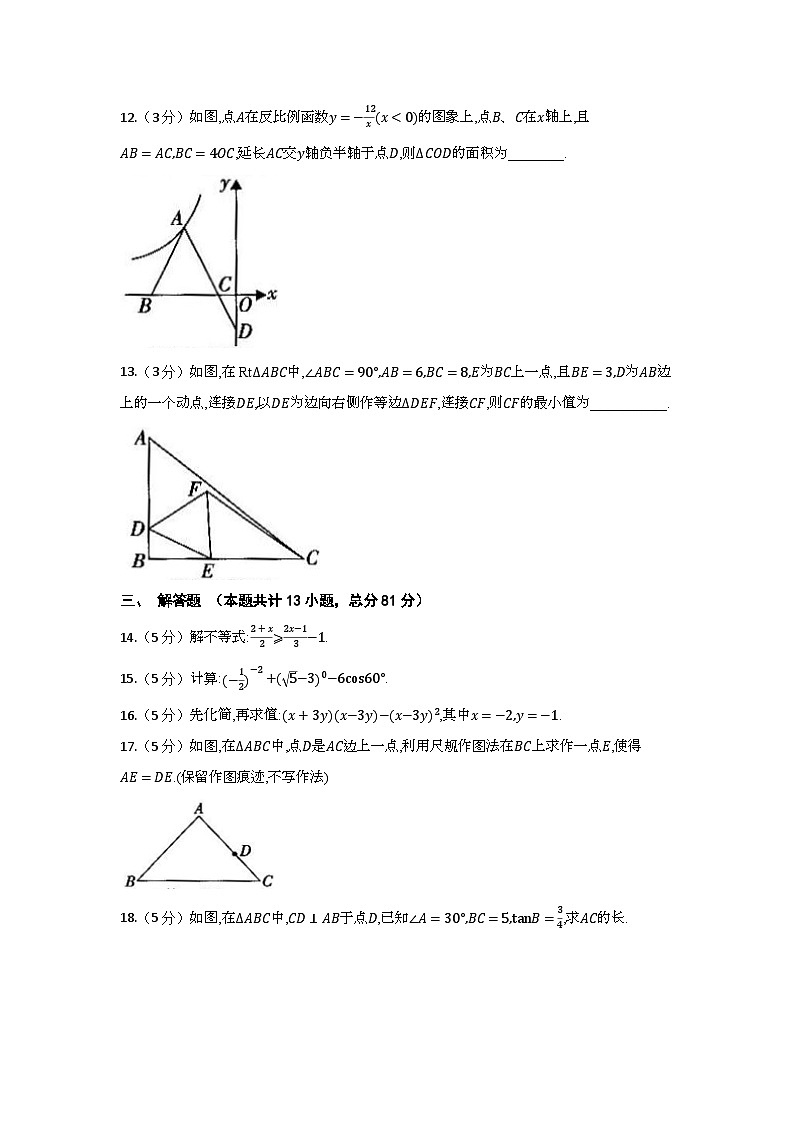
12.(3分)如图,点A在反比例函数y=−12x(x<0)的图象上,点B、C在x轴上,且AB=AC,BC=4OC,延长AC交y轴负半轴于点D,则ΔCOD的面积为________.
13.(3分)如图,在RtΔABC中,∠ABC=90°,AB=6,BC=8,E为BC上一点,且BE=3,D为AB边上的一个动点,连接DE,以DE为边向右侧作等边ΔDEF,连接CF,则CF的最小值为___________.
三、 解答题 (本题共计13小题,总分81分)
14.(5分)解不等式:2+x2⩾2x−13−1.
15.(5分)计算:(−12)−2+(5−3)0−6cs60°.
16.(5分)先化简,再求值:(x+3y)(x−3y)−(x−3y)2,其中x=−2,y=−1.
17.(5分)如图,在ΔABC中,点D是AC边上一点,利用尺规作图法在BC上求作一点E,使得AE=DE.(保留作图痕迹,不写作法)
18.(5分)如图,在ΔABC中,CD⊥AB于点D,已知∠A=30°,BC=5,tanB=34,求AC的长.
19.(5分)如图,ΔABC是等腰直角三角形,∠ABC=90°,点E是BC上一点,延长AB至点F,使得BF=BE,连接AE,CF,求证:AE=CF.
20.(5分)又是一年春来早,油菜花开万里香.为方便游客赴汉中踏青赏花,加开多趟列车,目前,西安至汉中每日往返开行动车组列车138趟,实现“公交化”开行.明明和爸爸、妈妈、爷爷、奶奶搭乘高铁外出赏花,爸爸在网上给五人购票时,五人的座位恰好位于同一车相的同一排(如图是高铁座位示意图),明明进人该车相后,可以从这五个座位中随机选择一个,每一个座位被选择的可能性相同.
(1)明明选择的座位佮好是座位A的概率是_________.
(2)明明坐下后,奶奶从剩下的四个座位中随机选择一个坐下,用列表法或画树状图法求明明和奶奶的座位相邻(过道两侧也可认为是座位相邻)的概率.
21.(6分)小雁塔位于唐长安城安仁坊(今陕西省西安市南郊)荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.一个晴朗的周末,王老师带领学生以小组为单位进行测量物体高度的实践活动,准备测量小雁塔的高度AB,他们带的测量工具有卷尺、测倾器、平面镜、标杆.
你选择的是_______组中的方法计算小雁塔的高度AB,请写出解答过程.(结果精确到0.1m)
22.(7分)小美在阅读物理课外书时,了解到在弹性限度内,弹簧的长度与所挂物体质量之间满足一次函数关系.她通过实验验证了这个事实,部分测量结果如表所示:
(1)根据所测量的数据,求该弹簧的长度y(cm)与所挂物体质量x(kg)之间的函数关系式;
(2)小美的妈妈在市场买了一些水果,小美将该水果放在袋中(袋子的质量忽略不计)挂到该弹簧下(在弹性限度内),并测得弹簧的长度为11.5cm.请你计算出小美的妈妈购买水果的质量.
23.(7分)2024年3月5日上午,国务院总理李强代表国务院在十四届全国人大二次会议上作政府工作报告,提到“深化全民阅读活动”.某校为了解全校学生每周的课外阅读时间情况,随机调查了部分学生每周课外阅读的时间,根据调查结果绘制了如下不完整的频数分布表和频数分布直方图.
请根据图表中的信息解答下列问题:
(1)频数分布表中的a=_______,补全频数分布直方图;
(2)被调查的这些学生每周课外阅读时间的中位数落在第_______组,求被调查的这些学生每周课外阅读时间的平均数(以每组的组中值为该组阅读的平均时间,例如第一组每周课外阅读的平均时间为45min);
(3)若该校共有1800名学生,试估计该校学生每周课外阅读时间不少于120min的学生人数.
24.(8分)如图,在RtΔABC中,∠ACB=90°,以AC为直径的⨀O与AB边交于点D,过点D作⨀O的切线,交BC于点E,连接OD.
(1)求证:∠BDE=∠B;
(2)若四边形CODE是正方形,AB=22,求DE的长.
25.(8分)如图,已知抛物线交x轴于A、B两点,交y轴于C点,点B的坐标为(3,0),OC=2,AB=4,点D为抛物线的顶点.
(1)求抛物线的函数表达式;
(2)若直线BC与抛物线的对称轴交于点E,点P是抛物线上的动点,点Q是直线BC.的动点,是否存在以D、E、P、Q为顶点的四边形是以DE为边的平行四边形,若存在,求出点Q的坐标;若不存在,请说明理由.
26.(10分)【问题提出】
(1)如图1,AC是菱形ABCD的对角线,则SΔABC_____SΔADC;(填“ > ”“ < "或“=”);
【问题探究】
(2)如图2,正方形ABCD的边长为4,点G在AD的延长线上,且DG=2,过点G的直线分别交边AB、CD于点E、F,若EF恰好将正方形ABCD的面积平分,求AE的长;
【问题解决】
(3)某公园有一片空地,其形状如图3所示,由矩形ABCD和以EF为直径的半圆构成,点E、F在AD上,公园规划人员欲将这块空地打造成花海供人们观赏,已知花海的人口在半圆上的点G处,EG^=FG^,要在BC边上找一点M,再沿GM修一条小路(小路的宽度忽略不计),使得GM将这块空地分成面积相等的两部分,用于种植不同的花,已知AB=80m,BC=140m,EF=2DF=40m,请你在图中找出点M的位置,并计算出小路GM的长.(结果保留根号)
答案
一、 单选题 (本题共计8小题,总分24分)
1.(3分)【答案】C
2.(3分)【答案】B
3.(3分)【答案】A
4.(3分)【答案】D
5.(3分)【答案】B
6.(3分)【答案】A
7.(3分)【答案】C
8.(3分)【答案】D
二、 填空题 (本题共计5小题,总分15分)
9.(3分)【答案】−π<−5<0<2
10.(3分)【答案】1.5×108
11.(3分)【答案】45
12.(3分)【答案】1
13.(3分)【答案】112(或5.5)
【解析】以CE为边在CE上方作等边ΔECG,过G作GM⊥AB于点M,GN⊥EC于点N,连接DG,易得四边形MGNB是矩形,由等边三角形的性质可得EN=NC=2.5,∠DEF=∠CEG=60°,则∠DEG=∠FEC,可得ΔDEG≅ΔFEC,则CF=DG,当DG⊥AB时,DG最小,即CF最小,此时D与M重合,从而得到CF的最小值为GM=BN=BE+EN=5.5.
三、 解答题 (本题共计13小题,总分81分)
14.(5分)【答案】解:去分母,得3(2+x)⩾2(2x−1)−6,
去括号,得6+3x⩾4x−2−6,
移项,合并同类项,得−x⩾−14,
系数化为1,得x⩽14.
15.(5分)【答案】解:原式=4+1−6×12
=4+1−3
=2.
16.(5分)【答案】解:原式=x2−9y2−(x2−6xy+9y2)
=x2−9y2−x2+6xy−9y2
=6xy−18y2,
当x=−2,y=−1时,
原式=6×(−2)×(−1)−18×(−1)2=12−18=−6.
17.(5分)【答案】解:如图所示,点E即为所求.
18.(5分)【答案】解:∵CD⊥AB,tanB=34,
∴设CD=3x,BD=4x,CD2+BD2=BC2,即(3x)2+(4x)2=52,解得x=1(负值舍去),
∴CD=3.
∵CD⊥AB,∠A=30°,
∴AC=2CD=6.
19.(5分)【答案】证明:∵ΔABC是等腰直角三角形,∠ABC=90°,
∴AB=CB,∠CBF=∠ABC=90°.
在ΔABE和ΔCBF中,AB=CB,∠ABE=∠CBF,BE=BF,
∴ΔABE≅ΔCBF(SAS),
∴AE=CF.
20.(5分)(1)解:15.
(2)列表如下:
由表可知共有20种等可能结果,其中明明和奶奶的座位相邻(过道两侧也认可是座位相邻)的结果有8种,
∴明明和奶奶的座位相邻(过道两侧也认可是座位相邻)的概率是820=25.
21.(6分)【答案】解:甲.
∵CD⊥BD,AB⊥BD,
∴∠ABE=∠CDE=90°.
∵∠AEB=∠CED,
∴ΔABE∼ΔCDE,
∴ABCD=BEDE,䀂
解得AB≈43.3(m),
∴小雅塔的高度AB约为43.3m.
乙.
由题意可得四边形BDCE是矩形,则CE=BD=32m,BE=CD=1.7m.
在RtΔACE中,tan∠ACE=AECE,即tan53°=AE32≈1.3,
∴AE≈41.6(m),
∴AB=AE+BE≈41.6+1.7=43.3(m),
∴小㕍塔的高度AB约为43.3m.
22.(7分)(1)解:设弹簧的长度y(cm)与所挂物体质量x(kg)之间的函数关系式为y=kx+b(k≠0),将(0,7),(1,7.5)代入得:{7=b,7.5=k+b,
解得{k=0.5,b=7,
∴该弹簧的长度y(cm)与所挂物体质量x(kg)之间的函数关系式为y=0.5x+7.
(2)将y=11.5代入y=0.5x+7得,
11.5=0.5x+7,
解得x=9.
∴小美的妈妈购买的水果质量是9kg.
23.(7分)(1)解:14.
(2)三(或90⩽t<120).
14+7+14+9+6×(45×4+75×7+105×14+135×9+165×6)=109.5(min),
∴被调查的这些学生每周课外阅读时间的平均数为109.5min.
(3)1800×9+640=675(名),
∴估计该校学生平均每周课外阅读时间不少于120min的学生有675名.
24.(8分)(1)证明:∵DE是⨀O的切线,
∴∠ODE=90°,
∵∠ACB=90°,
∴∠OAD+∠B=90°.
∵OA=OD,
∴∠OAD=∠ADO,
∴∠BDE=∠B.
则∠ADO+∠BDE=90°.
(2)解:∵四边形CODE是正方形,
∴CE=DE=OD=OC=OA,∠COD=∠CED=90°,
∴OD//BC,DE//AC,则OD和DE是ΔABC的中位线.
∵DE=OD,
∴AC=BC,则ΔABC是等腰直角三角形.
∵AB=22,
∴AC=BC=2,
∴DE=12AC=1.
25.(8分)(1)解:∵点B坐标为(3,0),AB=4,点C在y轴上,OC=2,
∴点A的坐标为(−1,0),点C的坐标为(0,2).设拖物线的函数表达式为y=ax2+bx+2,
将A(−1,0)和B(3,0)代入,
得{a−b+2=0,9a+3b+2=0,解得{a=−23,b=43,
∴拋物线的函数表达式为y=−23x2+43x+2.
(2)存在以D、E、P、Q为顶点的四边形是以DE为边的平行四边形.
抛物线y=−23x2+43x+2=−23(x−1)2+83,
∴抛物线的顶点D的坐标为(1,83).
设直线BC的函数表达式为y=kx+t,
将C(0,2),B(3,0)代入,得{3k+t=0t=2,
解得{k=−23,t=2,
∴直线BC的函数表达式为y=−23x+2.当x=1时,y=−23×1+2=43,
∴点E的坐标为(1,43),则DE=83−43=43.
∵以D、E、P、Q为顶点的四边形是以DE为边的平行四边形,
∴PQ//y轴,且PQ=DE=43,
设P(m,−23m2+43m+2),则Q(m,−23m+2),
当点P在点Q上方时,PQ=−23m2+43m+2−(−23m+2)=−23m2+2m,则−23m2+2m=43,解得m=2或m=1(舍),
∴点Q的坐标为(2,23).
当点P在点Q下方时,PQ=−23m+2−(−23m2+43m+2)=23m2−2m,则23m2−2m=43,解得m=3±172,
∴点Q的坐标为(3+172,3−173)或(3−172,3+173).
综上可得:存在以D、E、P、Q为项点的四边形是以DE为边的平行四边形,点Q的坐标为(2,23)或(3+172,3−173)或(3−172,3+173).
26.(10分)【答案】(1)解:=.
(2)连接AC交EF于点O.
∵EF将正方形ABCD的面积平分,AC为正方形的对角线,
∴O为AC的中点,
∴OA=OC.
∵四边形ABCD是正方形,
∴∠BAG=∠ADC=∠FDG=90°,AB//CD,
∴∠EAO=∠FCO,∠DFG=∠AEG,
∴ΔAEG∼ΔDFG,
∴DFAE=DGAG=26=13.
在ΔAOE和ΔCOF中,∠AOE=∠COF,OA=OC,∠EAO=∠FCO,
∴ΔAOE≅ΔCOF(ASA),
∴AE=CF,
则DFAE=DFCF=13,即DF4−DF=13,
解得DF=1,则AE=CF=4−1=3.
(3)连接AC、BD交于点O,过点G作GP⊥AD于点P,连接PO并延长交BC于点Q.
易得GP将半圆形分成面积相等的两部分,PQ将矩形ABCD分成面积相等的两部分,∴折线GP−PQ将这块空地的面积分成相等的两部分,
连接GQ,过点P作PM//GQ交BC边于点M,连接GM交PQ于点N.
∵PM//GQ,
∴SΔGPM=SΔQPN,
∴SΔGPM−SΔPWN=SΔQPM−SΔPMN,即SΔGPN=SΔQMN,
∴GM将这块空地的面积分成相等的两部分.
延长GP交BC于点H,则GH⊥BC,易得四边形CDPH是矩形,则PH=CD=AB,CH=DP.
∵AB=80m,BC=140m,EF=2DF=40m,
∴DF=PF=PE=GP=20m,BQ=DP=DF+PF=40m,PH=AB=80m,CH=DP=40m,
∴GH=GP+PH=20+80=100(m),QH=BC−BQ−CH=140−40−40=60(m).
∵PM//GQ,
∴∠HPM=∠HGQ.
又∵∠PHM=∠GHQ=90°,
∴ΔPHM∽ΔGHQ,
∴PHGH=MHQH,即80100=MH60,
∴MH=48m,
∴GM=MH2+CH2=482+1002=4769(m),
即小路GM的长为4769m.
2024年初中数学学业水平考试全真模拟试题(含答案): 这是一份2024年初中数学学业水平考试全真模拟试题(含答案),共14页。试卷主要包含了 单选题, 填空题, 解答题等内容,欢迎下载使用。
37,2024年湖南省长沙市 初中学业水平考试数学全真模拟(三): 这是一份37,2024年湖南省长沙市 初中学业水平考试数学全真模拟(三),共12页。试卷主要包含了4×104B.0,5分C.89分D.89等内容,欢迎下载使用。
37,2024年陕西省初中学业水平考试全真模拟(一)数学: 这是一份37,2024年陕西省初中学业水平考试全真模拟(一)数学,共6页。












