2024年甘肃省武威市凉州区永昌九年制学校教研联片九年级中考三模数学试题

这是一份2024年甘肃省武威市凉州区永昌九年制学校教研联片九年级中考三模数学试题，共12页。试卷主要包含了选择题，填空题，计算题，作图题，解答题等内容，欢迎下载使用。

一、选择题(共10题；共30分)
1．（3分）5G是第五代移动通信技术，5G网络理论下载速度可以达到每秒1300000KB以上.用科学记数法表示1300000是（ ）
A．13×105B．1.3×105C．1.3×106D．1.3×107
2．（3分）剪纸是中国优秀的传统文化．下列剪纸图案中，是中心对称图形的是（ ）
A． B． C． D．
3．（3分）单项式-12x3y的系数和次数分别是（ ）
A．-12，4B．-12，3C．12，3D．12，4
4．（3分）已知关于x的不等式组4x−a<3,12x+5⩾6无解，则a的取值范围是（ ）
A．a<5B．a⩽5C．a>5D．a⩾5
5．（3分）如图，正五边形ABCDE中，F为CD边中点，连接AF，则∠BAF的度数是（ ）
A．50°B．54°C．60°D．72°
6．（3分）如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（ ）
A．OA＝OC，OB＝OD B．AB＝CD，AO＝CO
C．AB＝CD，AD＝BC D．∠BAD＝∠BCD，AB∥CD
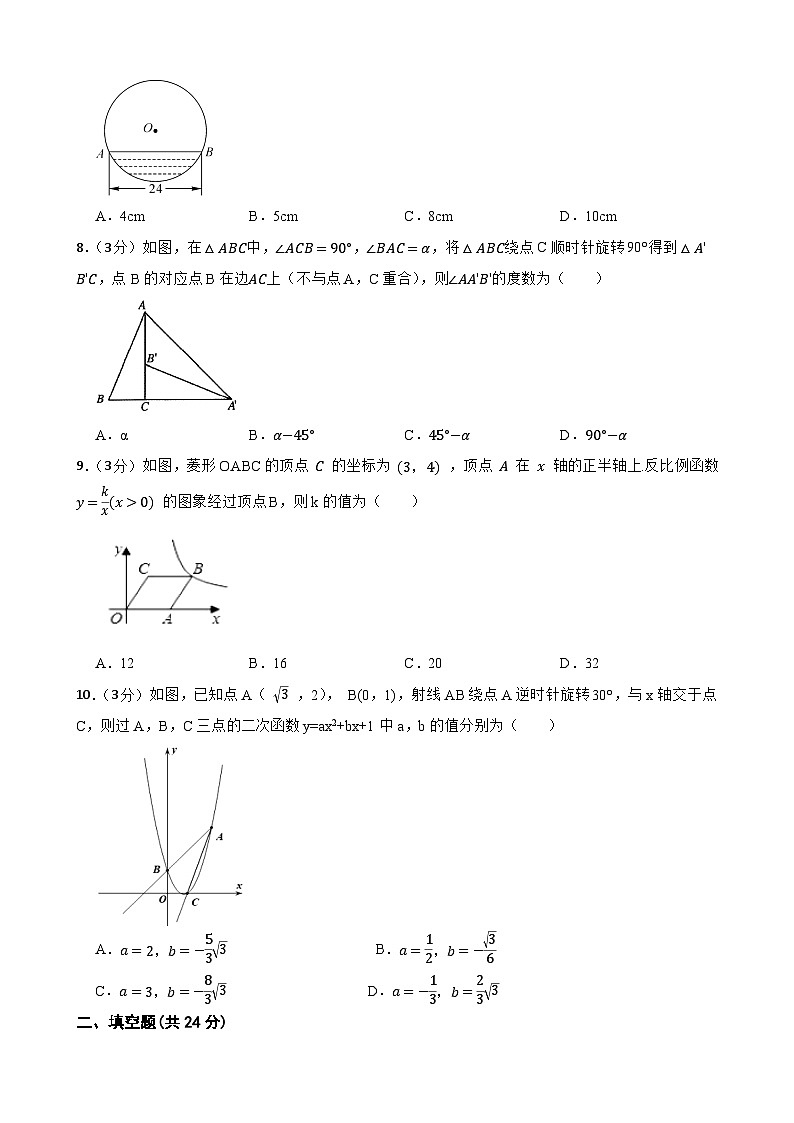
7．（3分）往直径为26cm的圆柱形容器内装入一些水以后，截面如图所示.若水面宽 AB=24cm ，则水的最大深度为（ ）
A．4cmB．5cmC．8cmD．10cm
8．（3分）如图，在△ABC中，∠ACB=90°，∠BAC=α，将△ABC绕点C顺时针旋转90°得到△A'B'C，点B的对应点B在边AC上（不与点A，C重合），则∠AA'B'的度数为（ ）
A．αB．α−45°C．45°−αD．90°−α
9．（3分）如图，菱形OABC的顶点 C 的坐标为 (3，4) ，顶点 A 在 x 轴的正半轴上.反比例函数 y=kx(x>0) 的图象经过顶点B，则k的值为（ ）
A．12B．16C．20D．32
10．（3分）如图，已知点A（ 3 ，2）， B(0，1)，射线AB绕点A逆时针旋转30°，与x轴交于点C，则过A，B，C三点的二次函数y=ax2+bx+1中a，b的值分别为（ ）
A．a=2，b=−533 B．a=12，b=−36
C．a=3，b=−833 D．a=−13，b=233
二、填空题(共24分)
11．（3分）若m与-2互为相反数，则m的值为 。
12．（3分）请写出关于x，y的二元一次方程 x−y=2 的一个解： .
13．（3分）过某个多边形一个顶点的所有对角线，将这个多边形分成7个三角形，这个多边形是 边形．
14．（3分）因式分解： 2x2−2= ；
15．（3分）如图，已知矩形ABCD，AB=9，AD=4，E为CD边上一点，CE=6，点P从B点出发，以每秒1个单位的速度沿着BA边向终点A运动，连接PE，设点P运动的时间为t秒，则当t的值为 时，△PAE是以PE为腰的等腰三角形．
16．（3分）已知：一次函数 y=kx+b 的图象与直线 y=−2x+1 平行，并且经过点(0，4)，那么这个一次函数的解析式是 .
17．（3分）如图，AB，BC是⊙O的两条弦，AB垂直平分半径OD，∠ABC＝75°，BC＝ 42 cm，则OC的长为 cm．
18．（3分）如图，在同一时刻，测得小华和旗杆的影长分别为1m和6m，小华的身高约为1.6m，则旗杆的高约为 m.
三、计算题(共8分)
19．（8分）（1）（4分）计算：|−2|+(13)0−9+2sin30°；
（2）（4分）解方程：x−2x+3−4x−3=1．
四、作图题(共6分)
20．（6分）如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A(1，1)，B(4，3)，C(2，4).
（1）（3分）请作出△ABC绕O点逆时针旋转90°的△A1B1C1，并求出线段AB扫过的面积.
（2）（3分）以点O为位似中心，将△ABC扩大为原来的2倍，得到△A2B2C2，△A2B2C2在y轴的左侧.
五、解答题(共52分)
21．（6分）已知：如图，点D在△ABC的BC边上，AC∥BE，BC=BE，∠ABC=∠E，求证：AB=DE．
22．（6分）如图， 四边形ABCD是矩形， 把矩形沿对角线AC折叠， 点B落在点E处，CE与AD相交于点O．
（1）（3分）求证：AO=CO
（2）（3分）若∠OCD=30∘，AB=3，求△AOC的面积．
23．（6分）两年前生产1吨甲种药品的成本是5000元，生产1吨乙种药品的成本是6000元，随着生产技术的进步，现在生产1吨甲种药品的成本是4050元，生产1吨乙种药品的成本是4860元，哪种药品成本的年平均下降率较大？
24．（8分）如图，直角三角形ABC中，∠C＝90°，点E为AB上一点，以AE为直径的⊙O上一点D在BC上，且AD平分∠BAC．
（1）（4分）证明：BC是⊙O的切线；
（2）（4分）若BD＝4，BE＝2，求AB的长．
25．（8分）如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．若AE=1，求FM的长．
26．（8分）某校在一次大课间活动中，采用了四种活动形式：A、跑步，B、跳绳，C、做操，D、游戏．全校学生都选择了一种形式参与活动，小杰对同学们选用的活动形式进行了随机抽样调查，根据调查统计结果，绘制了不完整的统计图．
请结合统计图，回答下列问题：
（1）（3分）本次调查学生共 人，a= ，并将条形图补充完整；
（2）（2分）如果该校有学生2000人，请你估计该校选择“跑步”这种活动的学生约有多少人？
（3）（3分）学校让每班在A、B、C、D四种活动形式中，随机抽取两种开展活动，请用树状图或列表的方法，求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率．
27．（10分）如图，在平面直角坐标系中，已知抛物线y＝ax2+bx+2与x轴相交于A（﹣1，0），B（4，0）两点，与y轴交于点C．
（1）（3分）求抛物线的解析式；
（2）（3分）点P是直线BC上方抛物线上一动点，连接PB，PC，求△PBC面积的最大值以及此时点P的坐标；
（3）（4分）抛物线上是否存在点Q，使∠QCB＝45°？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
答案
1-5 CDABB 6-10 BCCDA
11．2 12．x=2y=0 13．九 14．2(x+1)(x−1)
15．t=3或t=296 16．y=−2x+4 17．4cm 18．9.6
19．（1）1；（2）当x=13时，(x+3)(x−3)≠0，故原方程的解为x=13．
20．（1）∵△ABC的三个顶点坐标分别是A(1，1)，B(4，3)，C(2，4)
∴△ABC绕O点逆时针旋转90°，得A1(−1，1)，B1(−3，4)，C1(−4，2)
如图1所示：

图1 图2
△A1B1C1即为所求
∵A(1，1)，B(4，3)
∴OA2=1+1=2，OB2=42+32=25
线段AB扫过的面积=90×π(OB2−OA2)360=14π×23=234π；
（2）∵△ABC的三个顶点坐标分别是A(1，1)，B(4，3)，C(2，4)
∴A2(−2，2)，B2(−8，−6)，C2(−4，−8)
如图2所示， △A2B2C2即为所求.
21．∵BE∥AC，
∴∠C=∠DBE．
在△ABC和△DEB中，
∠C=∠DBEBC=EB∠ABC=∠E ，
∴△ABC≌△DEB，
∴AB=DE．
22．1．（1）∵四边形ABCD是矩形，
∴AD∥BC，
∴∠DAC=∠BCA，
又由折叠可知∠BCA=∠ECA，
∴∠DAC=∠ECA，
∴AO=CO
（2）在Rt△COD中，∠D=90°,∠OCD=30°，
∴OD=12OC，
又∵AB=CD=3，
在Rt△COD中，由勾股定理可得(12OC)2=OC2−(3)2，解得OC=2，
∴AO=OC=2，
∴S△AOC=12AO·CD=12×2×3=3
23．设甲种药品成本的年平均下降率为x，
根据题意得：5000（1﹣x）2=4050，
解之得：x=1.9（舍去）x=0.1=10%，
所以甲种药品成本的年平均下降率约为10%；
设乙种药品成本的年平均下降率为y，
根据题意得：6000（1﹣y）2=4860
解之得：y=1.9（舍去）y=0.1=10%，
所以乙种药品成本的年平均下降率约为10%；
答：甲乙两种药品成本的年平均下降率一样大
24．（1）连接OD，
AD平分∠BAC ∴∠1＝∠2
∵OA＝OD ∴∠2＝∠3 ∴∠1＝∠3，
∴AC//OD∵∠C＝90° ∴∠ODE＝90°，即OD⊥BC，
∵OD是半径 ∴BC是⊙O的切线，
（2）设OD＝OE＝r，
在Rt△ODB中，BD＝4，BE＝2，故OB＝r＋2
由勾股定理，得：r2+42=(r+2)2
解之，得：r＝3故OD＝OA＝OE＝3，AB＝6＋2＝8．
25．∵∆DAE逆时针旋转90°得到∆DCE，
∴∠FCM=∠FCD+∠DCM=180°，
∴F、C、M三点共线，
∴DE=DM，∠EDM=90°，
∴∠EDF+∠FDM=90°，
∵∠EDF=45°，
∴∠FDM=∠EDF=45°，
在∆DEF和∆DMF中，
DE=DM∠EDF=∠FDMDF=DF
∴∆DEF≌∆DMF（SAS），
∴EF=MF，
设EF=MF=x，
∵AE=CM=1，且BC=3，
∴BM=BC+CM=4，
∴BF=BM-MF=BM-EF=4-x，
∵EB=AB-AE=3-1=2，
在Rt∆EBF中 EB2+BF2=EF2
即 22+(4−x)2=x2
解得x= 52 ，
∴FM= 52
26．（1）300；10；
（2）2000×40%=800（人），
（3）画树状图为：
共有12种等可能的结果数，其中每班所抽到的两项方式恰好是“跑步”和“跳绳”的结果数为2，
所以每班所抽到的两项方式恰好是“跑步”和“跳绳”的概率=212=16．
27．（1）把A（﹣1，0），B（4，0）代入y＝ax2+bx+2得：
a−b+2=016a+4b+2=0，，
解得a=−12b=32，
∴抛物线的解析式为y=−12x2+32x+2；
（2）过P作PK∥y轴交BC于K，如图：
在y=−12x2+32x+2中，令x＝0得y＝2，
∴C（0，2），
由B（4，0），C（0，2）得直线BC解析式为y=−12x+2，
设P（t，−12t2+32t+2），则Kt，−12t+2，
∴PK＝−12t2+32t+2−−12t+2=−12t2+2t
∴S△PBC＝12PK⋅xB−xC=12×−12t2+2t×4=−t2+4t=−(t−2)2+4，
∵﹣1＜0，
∴当t＝2时，S△PBC取最大值4，此时P（2，3），
∴△PBC面积的最大值为4，此时点P的坐标为（2，3）；
（3）抛物线上存在点Q，使∠QCB＝45°，理由如下：
当Q在BC上方时，过B作BT⊥CQ于T，过T作MN⊥y轴于N，过B作BM⊥MN于M，如图：
∵∠QCB＝45°，
∴△BCT是等腰直角三角形，
∴∠BTC＝90°，BT＝CT，
∴∠CTN＝90°﹣∠BTM＝∠TBM，
∵∠M＝∠TNC＝90°，
∴△BTM≌△TCN（AAS），
∴BM＝NT，TM＝CN，
设T（m，n），则NT＝m，BM＝n，
∵B（4，0），C（0，2），
∴TM＝MN﹣NT＝4﹣m，CN＝ON﹣OC＝n﹣2，
∵BM＝NT，TM＝CN，
∴n=m4−m=n−2，，
解得m=3n=3
∴T（3，3），
由C（0，2），T（3，3）得直线CT解析式为y=13x+2，
联立y=13x+2y=12x2+32x+2，
解得x=73y=259，
∴Q（73，259）；
当Q在BC下方时，过B作BR⊥CQ于R，过R作SW⊥y轴于W，过B作BS⊥SW于S，如图：
同理可得△BSR≌△RWC（AAS），
∴BS＝RW，RS＝CW，
设R（p，q），
∴−q=p4−p=2−q，
解得p=1q=−1，，
∴R（1，﹣1），
∴直线CR解析式为y＝﹣3x+2，
联立y=−3x+2y=12x2+32x+2，
解得 x=9y=−25，
∴Q（9，﹣25），
综上所述，Q的坐标为（73，259）或（9，﹣25）．