2024年云南省玉溪市九年级初中学业水平考试模拟检测数学试题

这是一份2024年云南省玉溪市九年级初中学业水平考试模拟检测数学试题，共11页。试卷主要包含了水是生命之源，5，9D，按一定规律排列的单项式等内容，欢迎下载使用。

数学 试题卷
（全卷三个大题，共27个小题，共4页；满分100分，考试时间120分钟）
注意事项：
1.本卷为试题卷，考生必须在答题卡上解题作答，答案书写在答题卡相应位置上，在试题卷、草稿纸上作答无效.
2.考试结束后，请将试题卷和答题卡一并交回.
一、选择题（本大题共15小题，每小题只有一个正确选项，每小题2分，共30分）
1.的绝对值是（ ）
A.6B.C.D.
2.四个实数，0，，2中，最大的数是（ ）
A.B.0C.D.2
3.春节是中华民族的传统节日，古人常用写“桃符”的方式来祈福避祸，而现在，人们常用贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿.下列“福”字的四种篆书图案中，可以看作轴对称图形的是（ ）
A.B.C.D.
4.2月24日元宵佳节，由玉溪聂耳教师合唱团、玉溪师范学院附属小学音声合唱团共同演唱的歌曲《小雅・鹿鸣》在央视元莦晚会中精彩亮相，纯净的歌声和清澈空灵的童声吟诵、古风古韵的民乐伴奏和清新质朴的舞美造型，让《小雅・鹿鸣》再度唱进全国人民的心里，截至2月25日8时，中央广播电视总台元宵晚会跨媒体直播总触达人次3.53亿次.将数字“3.53亿”用科学记数法表示为（ ）
A.B.C.D.
5.先贤孔子曾说过“鼓之舞之”，这是“鼓舞”一词最早的起源.如图1是喜庆集会时击鼓瞬间的情景及鼓的立体图形，该立体图形的主视图是（ ）
图1
A.B.C.D.
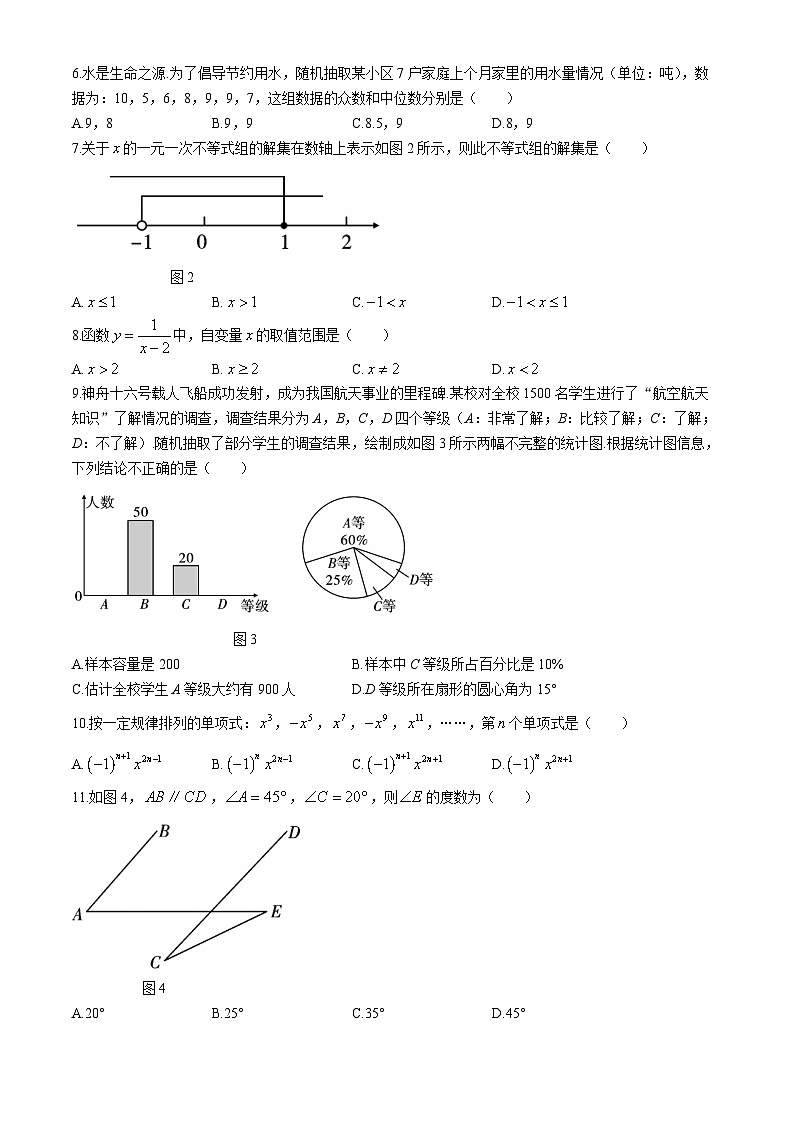
6.水是生命之源.为了倡导节约用水，随机抽取某小区7户家庭上个月家里的用水量情况（单位：吨），数据为：10，5，6，8，9，9，7，这组数据的众数和中位数分别是（ ）
A.9，8B.9，9C.8.5，9D.8，9
7.关于的一元一次不等式组的解集在数轴上表示如图2所示，则此不等式组的解集是（ ）
图2
A.B.C.D.
8.函数中，自变量的取值范围是（ ）
A.B.C.D.
9.神舟十六号载人飞船成功发射，成为我国航天事业的里程碑.某校对全校1500名学生进行了“航空航天知识”了解情况的调查，调查结果分为A，B，C，D四个等级（A：非常了解；B：比较了解；C：了解；D：不了解）.随机抽取了部分学生的调查结果，绘制成如图3所示两幅不完整的统计图.根据统计图信息，下列结论不正确的是（ ）
图3
A.样本容量是200B.样本中C等级所占百分比是10%
C.估计全校学生A等级大约有900人D.D等级所在扇形的圆心角为15°
10.按一定规律排列的单项式：，，，，，……，第个单项式是（ ）
A.B.C.D.
11.如图4，，，，则的度数为（ ）
图4
A.20°B.25°C.35°D.45°
12.下列运算正确的是（ ）
A.B.
C.D.
13.在同一平面直角坐标系中，一次函数与反比例函数的图象可能是（ ）
A.B.C.D.
14.若关于的一元二次方程有两个相等的实数根，则实数的值为（ ）
A.B.C.D.9
15.小明用一个圆心角为90°，半径为8的扇形围成一个圆锥的侧面，则这个圆锥的底面圆的半径是（ ）
A.1B.2C.3D.4
二、填空题（本大题共4小题，每小题2分，共8分）
16.分解因式：______.
17.计算：______.
18.如图5，是的直径，是的弦，于点，若，，则______.
图5
19.如图6，抛物线与轴交于点，则下列结论中正确的是______.（填序号）
图6
①；②；③；④.
三、解答题（本大题共8小题，共62分）
20.（本小题满分7分）
计算：.
21.（本小题满分6分）
如图7，，，，求证：.
图7
22.（本小题满分7分）
2024年春晚的吉祥物是名为“龙辰辰”的毛线玩偶，它的设计灵感源自生肖文化，汲取了中华优秀传统文化元素，展示出新时代中国人的精神风貌，为春晚增添了浓厚的节日氛围和美好寓意.某公司的两个车间负责生产“龙辰辰”吉祥物，已知甲车间每天生产吉祥物的数量是乙车间的1.5倍，甲车间生产600个吉祥物比乙车间生产1200个吉祥物少用1天.求甲、乙两车间每天各生产吉祥物多少个？
23.（本小题满分6分）
为落实“双减”政策要求，丰富学生课余生活，某校根据学生需求，组建了四个社团供学生选择：A（合唱社团）、B（硬笔书法社团）、C（舞蹈社团）、D（乒乓球社团）.
（1）小丽从这四个社团中随机选择一个，则选到舞蹈社团的概率为______；
（2）小明和小红分别从这四个社团中随机各选择一个参加活动，请用列表法或树状图法求他俩选到相同社团的概率.
24.（本小题满分8分）
如图8，，平分，且交于点，平分，且交于点，连接.
图8
（1）求证：四边形是菱形；
（2）若，，求平行线与间的距离.
25.（本小题满分8分）
如果鲜花有故乡，那么一定在云南，丰富多样的花卉就像妆点云南大地的画笔，把云南描绘的五彩斑斓.“三八”妇女节期间，某鲜花店计划购进康乃馨和玫瑰花两种鲜花，其中玫瑰花每束40元，购买康乃馨所需费用（单位：元）与购买数量（单位：束）的函数关系图象如图9所示.
图9
（1）求与的函数解析式（也称关系式）；
（2）该鲜花店计划购进康乃馨和玫瑰花共200束，若购买康乃馨的数量不超过150束，且不少于玫瑰花的数量，购买两种鲜花的总费用为，如何购买能使费用最少，并求出最少费用.
26.（本小题满分8分）
已知抛物线.
（1）当时，求该抛物线的对称轴；
（2）当该抛物线与轴两交点的横坐标都为正整数时，求整数的值.
27.（本小题满分12分）
如图10，四边形内接于，是的直径，，连接，过点的直线与的延长线交于点，且.
图10
（1）求的度数；
（2）求证：是的切线；
（3）猜想与、之间的数量关系，并说明理由.
2024年玉溪市初中学业水平考试模拟检测
数学参考答案
一、选择题（本大题共15小题，每小题只有一个正确选项，每小题2分，共30分）
二、填空题（本大题共4小题，每小题2分，共8分）
三、解答题（本大题共8小题，共62分）
20.（本小题满分7分）
解：原式（5分）
.（7分）
21.（本小题满分6分）
证明：如图1，，
图1
，
即，（2分）
在和中，
.（6分）
22.（本小题满分7分）
解：设乙车间每天生产吉祥物个，则甲车间每天生产吉祥物个，（1分）
由题意得：，（3分）
解得：，（4分）
经检验，是原方程的解，且符合题意，（5分）
，（6分）
答：甲车间每天生产吉祥物1200个，乙车间每天生产吉祥物800个.（7分）
23.（本小题满分6分）
解：（1）答案为：（2分）
（2）画树状图如图2：
图2
结果：
（4分）
共有16种等可能的结果，其中他俩选到相同社团的有4种结果，（5分）
所以他俩选到相同社团的概率为.（6分）
24.（本小题满分8分）
（1）证明：，
，.（1分）
、分别是、的平分线，
，，
，，
，，
.（2分）
，
四边形是平行四边形.（3分）
，
四边形是菱形.（4分）
（2）解：如图3，过点作于点，（5分）
图3
四边形是菱形，，，
，，，（6分）
，
，（7分）
，
即平行线与间的距离为.（8分）
25.（本小题满分8分）
解：（1）由图可得：当时，，（1分）
当时，设与的函数解析式为，
，（2分）
解得：，（3分）
与的函数解析式为：.（4分）
（2）设购买康乃馨的数量为束，则购买玫瑰花的数量为束，由题意得：
，且，解得：.（5分）
，（6分）
，随的增大而增大，
当时，最小，且最小值为：（元）.（7分）
答：购买康乃馨和玫瑰花各100束时，费用最少，最少费用为8600元.（8分）
26.（本小题满分8分）
解：（1）当时，，
抛物线的对称轴是直线.（4分）
（2）当时，
解得：，，（6分）
抛物线与轴两交点的横坐标都为正整数，
为正整数，
或2或4，（7分）
解得：或4或6，
综上，该抛物线与轴两交点的横坐标都为正整数时，整数的值为3或4或6.（8分）
27.（本小题满分12分）
（1）解：是的直径，
.（1分）
，
，（3分）
.（4分）
（2）证明：如图4，连接，（5分）
图4
是的直径.
，即.
，
，
又，
，
，（7分）
，
，
，即.
又是半径，
直线是的切线.（8分）
（3）答：.（9分）
理由：过点作交延长线于点，如图5，
图5
.
是的直径，
，
，
，
四边形内接于，
，
，
，（10分）
，，
，
，，
，（11分）
，
.（12分）
【备注】解答题每小题只给出了一种解法，其它解法只要步骤合理、解答正确均应得到相应的分数.
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案
A
D
C
B
B
A
D
C
D
C
B
D
A
C
B
题号
16
17
18
19
答案
1
2
②④