河南省南阳市淅川县2023-2024学年八年级下学期期中数学试题（原卷版+解析版）

这是一份河南省南阳市淅川县2023-2024学年八年级下学期期中数学试题（原卷版+解析版），文件包含河南省南阳市淅川县2023-2024学年八年级下学期期中数学试题原卷版docx、河南省南阳市淅川县2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

2．本试卷上不要答题，请按答题卡上注意事项的要求直接把答案写在答题卡上．答在试题卷上的答案无效．
一、选择题（本大题共10小题，每小题3分，共30分）
1. 若分式有意义，则x应满足的条件是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题主要考查分式有意义的条件：分母不能为0
【详解】解：∵x-2≠0，
∴x≠2，
故选A．
【点睛】本题考查的是分式有意义的条件，当分母不为0时，分式有意义．
2. 下列计算正确的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】此题考查分式的基本性质，分式的混合运算，关键是根据把分式的分子和分母扩大还是缩小相同的倍数，分式的值不变解答．分子和分母同乘以（或除以）一个不为0的数，分数值不变．
【详解】解：A、，错误；
B、，错误；
C、，错误；
D、，正确；
故选：D
3. 已知正比例函数的图象如图所示经过点(3，－3)，则这个函数的关系式为（ ）

A. y＝xB. y＝－xC. y＝－3xD. y＝3x
【答案】B
【解析】
【分析】首先根据图象是经过原点的直线可得此函数是正比例函数，所以设解析式为y=kx（k≠0），把图象所经过的点（3，-3）代入设出的函数解析式，计算出k的值，进而得到函数解析式．
【详解】设函数解析式为y=kx（k≠0），
∵图象经过（3，-3），∴-3=k×3，解得k=-1，
∴这个函数的关系式为y=-x，故选：B．
【点睛】此题主要考查了待定系数法求函数解析式，关键是掌握凡是图象经过的点必能满足解析式
4. 2023年9月，华为最新的发售，销量遥遥领先，其中使用的华为新麒麟芯片突破5纳米（1纳米毫米）制程工艺，数据“5纳米”用科学记数法表示为（ ）
A. 毫米B. 毫米C. 毫米D. 毫米
【答案】C
【解析】
【分析】本题考查了科学记数法；“将一个数表示成的形式，其中，为整数，这种记数的方法叫做科学记数法”，熟记科学记数法的定义是解题关键．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．根据科学记数法的定义即可得．
【详解】解：5纳米毫米．
故选：C．
5. 下列函数图像中，能反映等腰三角形顶角（度）与底角（度）之间函数关系的是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】等腰三角形的两个底角相等，由内角和定理可知：x+x+y=180，进而可得，y=180-2x，由y＞0得：x＜90，又x＞0，故0＜x＜90．
【详解】∵等腰三角形的两个底角相等，
∴y+2x=180°，
∴y=-2x+180°，
∵-2<0，180°>0，
∴图象经过一、二、四象限，
∵y>0，x>0，
∴0故只有B符合题意，
故选B.
【点睛】本题考查了一次函数的实际应用，熟练掌握一次函数的性质并注意自变量x的取值范围是解题关键．
6. 根据分式的基本性质，分式可变形为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题主要考查了分式的基本性质，分式的分子和分母同时乘以或除以同一个不为零的数或式子，分式的值不变，据此求解即可．
【详解】解：，
故选：D．
7. 在对物体做功一定的情况下，力F（N）与此物体在力的方向上移动的距离s（m）成反比例函数关系，其图象如图所示，点在其图象上，则当力达到10N时，物体在力的方向上移动的距离是（ ）
A. 2.4mB. 1.2mC. 1mD. 0.5m
【答案】B
【解析】
【分析】利用点P的坐标求出F=，当F=10时，即F==10，求出s，即可求解．
【详解】解：设函数的表达式F=，
将点P的坐标代入上式得：3=，解得k=12，
则反比例函数表达式为F=，
当F=10时，即F==10，
解得s=1.2（m），
故选：B．
【点睛】本题考查反比例函数系数k的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k|．
8. 如图，点A在反比例函数y＝的图象上，AB⊥x轴于点B，点C在x轴上，且CO＝OB，△ABC的面积为2，则k的值为（ ）
A. 4B. 3C. 2D. 1
【答案】C
【解析】
【分析】首先表示出BC，AB的长，再利用三角形面积得出k的值．
【详解】设CO=BO=a，则AB=，
∵△ABC的面积为2，
∴×2a×=2，
解得：k=2．
故选C．
【点睛】考查了反比例函数系数k的几何意义，正确表示出三角形面积是解题关键．
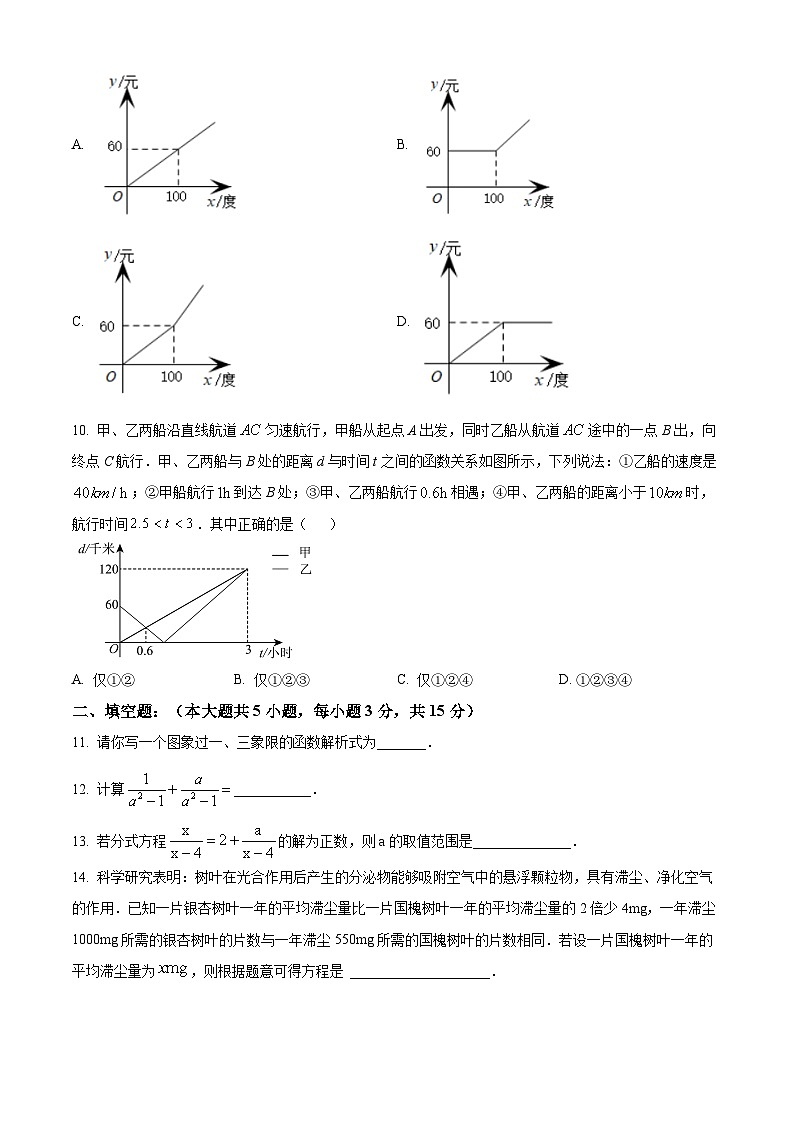
9. 为了节能减排，鼓励居民节约用电，某市出台了新的居民用电收费标准：（1）若每户居民每月用电量不超过100度，则按0.60元/度计算；（2）若每户居民每月用电量超过100度，则超过部分按0.8元/度计算（未超过部分仍按每度电0.60元/度计算），现假设某户居民某月用电量是x（单位：度），电费为y（单位：元），则y与x的函数关系用图象表示正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
详解】解：根据题意，当0≤x≤100时，y=0.6x，
当x＞100时，y=100×0.6+0.8（x﹣100）=60+0.8x﹣80=0.8x﹣20，
所以，y与x的函数关系为，
纵观各选项，只有C选项图象符合．
故选C．
【点睛】本题考查了分段函数以及函数图象，根据题意求出各用电量段内的函数解析式是解题的关键．
10. 甲、乙两船沿直线航道匀速航行，甲船从起点A出发，同时乙船从航道途中的一点B出，向终点C航行．甲、乙两船与B处的距离d与时间t之间的函数关系如图所示，下列说法：①乙船的速度是；②甲船航行到达B处；③甲、乙两船航行相遇；④甲、乙两船的距离小于时，航行时间．其中正确的是（ ）
A. 仅①②B. 仅①②③C. 仅①②④D. ①②③④
【答案】C
【解析】
【分析】本题考查了一次函数在行程问题中的应用，读懂图象、明确行程问题的基本数量关系并数形结合是解题的关键．
结合图形，分从乙走全程及时间得出乙的速度；从而可知时，乙走的路程，进而得出甲走的路程，从而可知甲的速度；根据题中对与时间的关系可判断甲乙两船航行0．6小时是否相遇；由前面求得的甲乙速度可判断甲、乙两船的距离不小于10千米的时间段．
【详解】解：乙船从到共用时3小时，走过路程为120千米，因此乙船的速度是40千米/时，①正确；
乙船经过小时走过千米，
甲船小时走过千米，
所以甲船的速度是千米/时，
开始甲船距点60千米，因此经过1小时到达点，②正确；
航行小时后，甲乙距点都为24千米，但是乙船在点前，甲船在点后，二者相距48千米，因此③错误；
开始后，甲乙两船之间的距离越来越小，甲船经过1小时到达点，此时乙离地40千米，航行小时后，
甲离地：千米，
乙离地：千米，此时两船相距10千米，
当时，甲乙的距离小于10，因此④正确；
综上所述，正确的说法有①②④．
故选：C．
二、填空题：（本大题共5小题，每小题3分，共15分）
11. 请你写一个图象过一、三象限的函数解析式为_______．
【答案】（答案不唯一）
【解析】
【分析】本题考查了本题考查了正比例函数的性质，根据正比例函数的性质求解．
【详解】解：图象过一、三象限的函数解析式为，
故答案为：（答案不唯一）．
12. 计算___________．
【答案】
【解析】
【分析】根据平方差公式对分母进行因式分解，然后约分即可．
【详解】解：
【点睛】此题主要考查了平方差公式的运用，涉及了分式的有关计算，熟练掌握平方差公式是解题的关键．
13. 若分式方程的解为正数，则a的取值范围是______________．
【答案】a＜8，且a≠4
【解析】
【详解】解：分式方程去分母得：x=2x-8+a，
解得：x=8-a，
根据题意得：8-a＞0，8-a≠4，
解得：a＜8，且a≠4．
故答案为：a＜8，且a≠4．
【点睛】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，根据分式方程解为正数求出a的范围即可．此题考查了分式方程的解，需注意在任何时候都要考虑分母不为0．
14. 科学研究表明：树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物，具有滞尘、净化空气的作用．已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4mg，一年滞尘1000mg所需的银杏树叶的片数与一年滞尘550mg所需的国槐树叶的片数相同．若设一片国槐树叶一年的平均滞尘量为，则根据题意可得方程是 ____________________．
【答案】
【解析】
【分析】根据一年滞尘所需的银杏树叶的片数与一年滞尘所需的国槐树叶的片数相同，列方程即可．此题主要考查了由实际问题抽象出分式方程，解题的关键是弄清题意，找到题目中的关键语句，列出方程．
【详解】解：设一片槐树叶一年平均滞尘量为，
则一片银杏树叶一年平均滞尘量为，
由题意得：．
故答案为：．
15. 如图，直线与轴，轴分别交于点和点，点在线段上，且点坐标为，点为线段的中点，点为上一动点，当的周长最小时，点的坐标为______．
【答案】
【解析】
【分析】本题考查了待定系数法求函数解析式、一次函数图象上点的坐标特征以及轴对称中最短路径问题，解题的关键是求出直线的解析式．本题属于基础题，难度不大，解决该题型题目时，找出点的坐标利用待定系数法求出函数解析式是关键．根据一次函数解析式求出点、的坐标，再由中点坐标公式求出点、的坐标，根据对称的性质找出点的坐标，结合点、的坐标求出直线的解析式，令即可求出的值，从而得出点的坐标．
【详解】解：作点关于轴的对称点，连接交轴于点，此时值最小，如图．
令中，则
点的坐标为；
令中，则，解得：，
点的坐标为．
点、分别为线段、的中点，
点，点．
点和点关于轴对称，
点的坐标为．
设直线的解析式为，
直线过点，，
，解得：，
直线的解析式为．
令，则，解得：，
点的坐标为，．
故选：，．
三、解答题：（本大题共8小题，共75分）
16. （1）
（2）
【答案】（1）；（2）
【解析】
【分析】本题主要考查分式的混合运算及实数的混合运算，解答的关键是对相应的运算法则的掌握．
（1）根据零指数幂及负指数幂的运算法则进行运算即可；
（2）根据分式的运算法则进行计算即可．
【详解】解：（1）原式，
；
（2）原式
17. 先化简，然后从﹣＜x＜的范围内选取一个合适的整数作为x的值代入求值．
【答案】x=-2时,原式=
【解析】
【详解】分析：先把的分子、分母分解因式，把通分，然后把除法转化为乘法约分化简，从﹣＜x＜中取一个使分式有意义的数代入到化简后的式子中计算即可.
详解：，
=，
=，
=，
=.
当x=-2时，原式=.
点睛：本题考查了分式化简求值，熟练掌握分式混合运算的运算法则是解答本题的关键，本题也考查了分式有意义的条件，取值时不能取-1,0，1三个数.
18. 解方程：．
【答案】无解
【解析】
【分析】本题的最简公分母是x-2，等式两边都乘以x-2，化简求解，最后检验即可．
【详解】解：原方程整理得：，
去分母得：，
移项合并得：，
解得：，
检验：把代入最简公分母中，
，
∴是增根，
∴原方程无解．
【点睛】本题主要考查的是分式方程，把分式方程转化为整式方程，最后检验是解答本题的关键是．
19. 已知y与x的函数关系式为
（1）若y是x的正比例函数，求m的值；
（2）若函数的图象过点，求m的值，并写出这个函数的解析式；
（3）若将（2）中的函数图象向上平移3个单位长度经过点，求n的值．
【答案】（1）
（2），
（3）
【解析】
【分析】本题主要考查了求一次函数解析式，一次函数图象的平移问题，求一次函数值，正比例函数的定义等等：
（1）根据形如的函数叫做正比例函数得到，解之即可得到答案；
（2）把代入函数解析式求出m的值即可求出对应的函数解析式；
（3）先根据平移方式求出平移后的解析式，进而求出当时，x的值即可得到答案．
【小问1详解】
解：∵函数是正比例函数，
∴，
∴；
【小问2详解】
解：∵函数的图像过点，
∴，
∴，
∴；
【小问3详解】
解：函数的函数图象向上平移3个单位长度后的解析式为，
在中，当时，，即．
20. 如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于、两点．
（1）求一次函数和反比例函数的解析式；
（2）观察图象，直接写出不等式的解集；
（3）若P是y轴上一点，且满足的面积是5，求点P坐标．
【答案】（1），；
（2）或；
（3）或
【解析】
【分析】此题考查了一次函数与反比例函数的交点问题，涉及的知识有：待定系数法求函数解析式，坐标与图形性质，以及三角形的面积求法，熟练掌握待定系数法是解本题的关键．
（1）可先把代入反比例函数解析式，求得的值，进而求得的值，把，两点分别代入一次函数解析式即可．
（2）利用图象法解决问题即可；
（3）令求出的值，确定出坐标，得到的长，三角形面积由三角形面积与三角形面积之和求出，由已知的面积求出的长，即可求出的长．
【小问1详解】
点在上，
，
反比例函数解析式为；
又点在上，
，
点的坐标为，
把和两点的坐标代入一次函数得
解得，
一次函数的解析为．
【小问2详解】
观察图象可知：不等式的解集为或；
【小问3详解】
如图，设一次函数与y轴交于点C，
对于一次函数，令，求出，
即，，
根据题意得：，
解得：，
所以，或．
21. 某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分先收取固定的制版费，再按印刷数量收取印刷费，乙厂直接按印刷数量收取印刷费．甲厂的总费用y1（干元）、乙厂的总费用y2（千元）与印制证书数量x（千个）的函数关系图分别如图中甲、乙所示．
（l）甲厂的制版费为 千元，印刷费为平均每个 元，甲厂的费用yl与证书数量x之间的函数关系式为 ．
（2）当印制证书数量不超过2千个时，乙厂的印刷费为平均每个 元；
（3）当印制证书数量超过2千个时，求乙厂的总费用y2与证书数量x之间的函数关系式；
（4）若该单位需印制证书数量为8千个，该单位应选择哪个厂更节省费用？请说明理由．
【答案】（1）1；0.5；y=0.5x+1；（2）1.5；（3）；（4）由图象可知，当x=8时，y1>y2，因此该单位选择乙厂更节省费用．
【解析】
【详解】试题分析：（1）由图得制版费是1千元，通过坐标（0,1）（2,2）求出函数解析式，印刷单价=（印刷费用-制版费）÷2000；
（2）由图像可知，用3千元÷2千个，即可得到乙厂的平均印刷费；
（3）设y2=kx+b，由图可知，当x=6时y1与y2相交，利用（1）中求出的函数关系式可求出相应的值，把这一点和（2,3）点代入设的解析式，即可求出相应的函数关系式；
（4） 分别求出甲乙两车的费用y关于证书个数x的函数，将x=8分别代入两个函数求值比较即可，可得出选择乙厂节省．
试题解析：
（1）1；0.5；y=0.5x+1；
（2）1.5；
（3）设y2=kx+b，
由图可知，当x=6时，y2=y1=0.5×6+1=4，
所以函数图象经过点（2,3）和（6,4）．
所以把（2,3）和（6,4）代入y2=kx+b，得，
解得，所以y2与x之间的函数关系式为 ．
（4）由图象可知，当x=8时，y1>y2，因此该单位选择乙厂更节省费用．
（求出当x=8时，y1和y2的值，用比较大小的方法得到结论也正确）
考点：一次函数的应用．
22. 某快递公司为了提高工作效率，计划购买A，B两种型号的机器人来搬运货物，已知每台A型机器人比每台B型机器人每天多搬运20吨，并且3台A型机器人和2台B型机器人每天共搬运货物460吨．
（1）求每台A型机器人和每台B型机器人每天分别搬运货物多少吨?
（2）每台A型机器人售价3万元，每台B型机器人售价2万元，该公司计划采购A，B两种型号的机器人共20台，必须满足每天搬运的货物不低于1800吨，该公司应该如何设计采购方案才能使得费用最低，最低费用是多少?
【答案】（1）100吨，80吨
（2）A种型号的机器人采购10台，B种型号的机器人采购10台时费用最低为50万元
【解析】
【分析】考查了二元一次方程组的应用及一次函数应用．解决问题的关键是读懂题意，找到关键描述语，找到所求的量的等量关系．列出对应的方程组，极值问题来利用函数的递增情况解决
（1）题目中的等量关系是：①每台型机器人比每台型机器人每天多搬运20吨，②3台型机器人和2台型机器人每天共搬运货物460吨．
（2）题目中的不等关系是：每天搬运的货物不低于1800吨，等量关系是：总费用型机器费用型机器费用，极值问题来利用函数的递增情况解决．
【小问1详解】
设每台型机器人每天搬运货物吨，每台型机器人每天搬运货物吨，
，
解得，
每台型机器人每天搬运货物100吨，每台型机器人每天搬运货物80吨；
【小问2详解】
设种机器人采购台，种机器人采购台，总费用为（万元），
．
解得：．
．
，
随着的减少而减少．
当时，有最小值，．
、两种机器人分别采购10台，10台时，所需费用最低，最低费用是50万元．
23. 我们把形如（，不为零），且两个解分别为，的方程称为“十字分式方程”．例如为十字分式方程，可化为，所以，．再如为十字分式方程，可化为，所以，．
应用上面的结论解答下列问题：
（1）若为十字分式方程，则 ， ；
（2）若十字分式方程的两个解分别为，，求的值；
（3）设为常数且，若关于的十字分式方程的两个解分别为，，求的值．
【答案】（1），
（2）
（3）4
【解析】
【分析】本题考查根与系数的关系，分式方程；理解“阅读材料”中的答题方法，能够将所求分式方程转化为求解是解题的关键．
（1）类比题目中“阅读材料”的答题方法即可求解．
（2）结合运用“阅读材料”即可求出和的值，并代数运算即可求解；
（3）善于观察并分析方程，即可求出和的值，代入运算即可求解．
【小问1详解】
解：可化，
，
经检验是该方程的解．
【小问2详解】
∵的两个解分别为，，
故，
．
【小问3详解】
原方程变为，
，
，
，
．