山东省烟台市招远市2023-2024学年下学期九年级期中考试数学试题

这是一份山东省烟台市招远市2023-2024学年下学期九年级期中考试数学试题，共7页。试卷主要包含了对于实数a，b定义新运算等内容，欢迎下载使用。

说明：1.考试时间120分钟，满分120分。
2.考试过程允许学生进行剪、拼、折叠等实验。
一、选择题（本大题共10个小题，每小题3分，满分30分）
1.下列关于x的方程是一元二次方程的是（ ）
A. x2+y-3=0 B. 3x(x-4) =0 C.+x=2 D. x3-3x+8=0
2.下列二次根式中，属于最简二次根式的是（ ）
A.13 B.13 C.3 D.27
3.如图，ABCD的对角线交于点O，下列条件不能判定ABCD 是菱形的是（ ）
A.AB = AD B.∠ABD = ∠ADB
C.∠AOB = 90° D.AB = CD
4.已知的整数部分是方程x2-5x-m=0的一个根，则该方程的另一根是（ ）
A.-1 B.1 C.2 D.3
6.如图，在正方形ABCD中，点E，F分别在BC和AD边上，BE=1，AF=5，AE//CF，则△ABE的面积为（ ）
A.6 B.5 C.3 D.
7.在对边不相等的四边形中，若四边形的两条对角线互相垂直，那么顺次连结四边形各边中点得到的四边形是（ ）
A.平行四边形B.矩形C.菱形D.正方形
8.对于实数a，b定义新运算：a*b=ab2-b，若关于x方程2*x=2k没有实数根，则k 的取值范围（ ）
9.当x=-2时，代数式x2+4x+8值是（ ）
A.19 B.21 C.27 D.29
10.已知，如图，点A，为x轴上一点，它的坐标为（1，0），过点A，作x轴的垂线与直线OM:y=x交于点B1，以线段A1B1为边作正方形A1B1C1A2；延长A2C1交直线OM于点B2，再以线段A2B2为边作正方形A2B2C2A3；延长A3C2交直线OM于点B3，再以线段A3B3为边作正方形A3B3C3A4….依此类推，C2024的坐标为（ ）
A.（22023，22023）B.（22023，22024）
C.（22024，22023）D.（22024，22024）
二、填空题（本大题共6个小题，每小题3分，满分18分）
11.若在实数范围内有意义，则m的取值范围是 .
12.关于x的一元二次方程x2 + bx +2c=0有两个相等的实数根，则b2-2（3+4c）的值为 .
13.在矩形ABCD中，对角线AC、BD相交于点O，过点A作AM⊥BD，交BD于点M，若∠MAD=5∠BAM，则∠MAO的度数为 .
14.已知 a 是方程x2-3x-2=0 的一个根，则3a2-9a+2024的值为 .
15.已知 ，则 xy= .
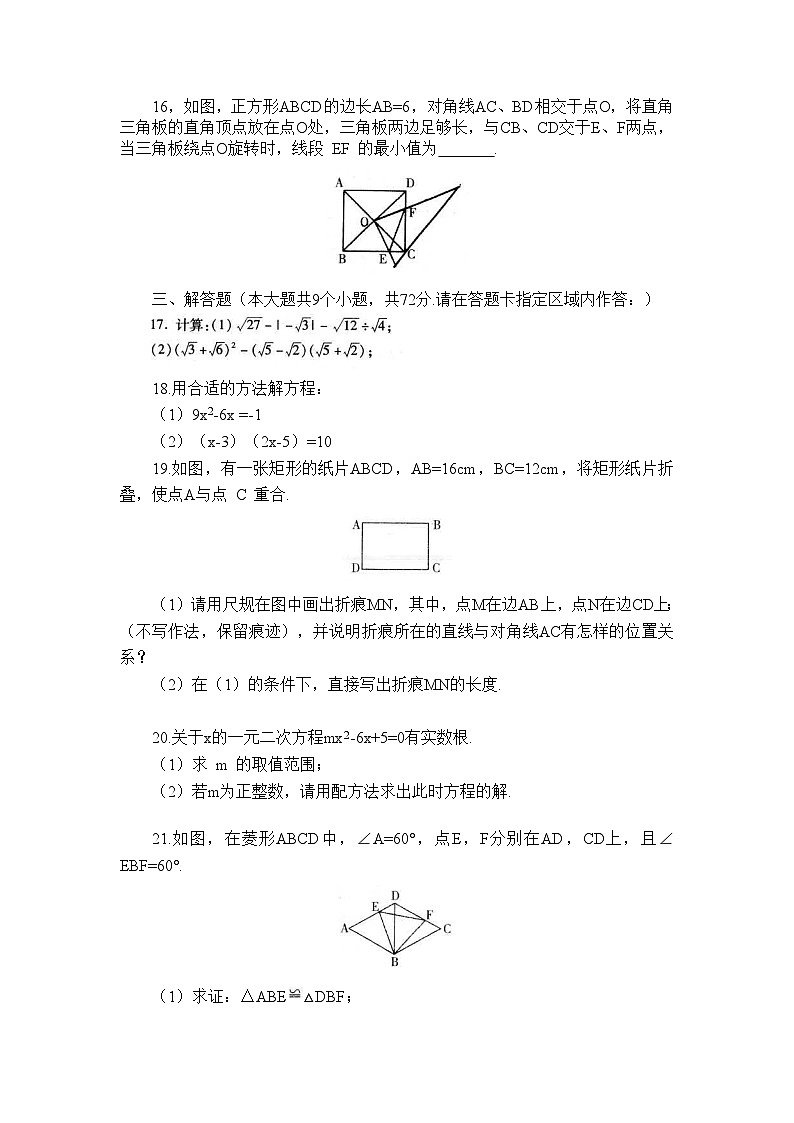
16，如图，正方形ABCD的边长AB=6，对角线AC、BD相交于点O，将直角三角板的直角顶点放在点O处，三角板两边足够长，与CB、CD交于E、F两点，当三角板绕点O旋转时，线段 EF 的最小值为 .
三、解答题（本大题共9个小题，共72分.请在答题卡指定区域内作答：）
18.用合适的方法解方程：
（1）9x2-6x =-1
（2）（x-3）（2x-5）=10
19.如图，有一张矩形的纸片ABCD，AB=16cm，BC=12cm，将矩形纸片折叠，使点A与点 C 重合.
（1）请用尺规在图中画出折痕MN，其中，点M在边AB上，点N在边CD上；（不写作法，保留痕迹），并说明折痕所在的直线与对角线AC有怎样的位置关系？
（2）在（1）的条件下，直接写出折痕MN的长度.
20.关于x的一元二次方程mx2-6x+5=0有实数根.
（1）求 m 的取值范围；
（2）若m为正整数，请用配方法求出此时方程的解.
21.如图，在菱形ABCD中，∠A=60°，点E，F分别在AD，CD上，且∠EBF=60°.
（1）求证：△ABE△DBF；
（2）若BE=10，试求出线段EF的长，并说明理由.
22.已知x=
（1）分别求 x+y，xy 的值
（2）利用（1）的结果求下列代数式的值： eq \\ac(○,1)x2y+xy2；
23.如图，菱形 ABCD 的对角线 AC，BD 相交于点 O，过点 D作 DE//AC，且 DE=AC，连接CE.
（1）求证：四边形 OCED为矩形.
（2）若菱形的面积是10，请求出矩形OCED的面积.
24.阅读理解：
我们解决某些数学题的时候，经常会遇到题目中的条件比较含糊，它们常常巧妙地隐蔽在题设的背后，不易被发现和运用，导致我们解题受阻，因此，挖掘题设中的隐含条件，应该成为我们必备的一种能力。请阅读下面的解题过程，体会如何发现隐含条件，并依次解决所给的问题.
化简：（）2-|1-a|.
解：由题意可知隐含条件1-5a≥0，解得：a≤
∴1-a＞0，
∴（）2-|1-a| =1-5a-（1-a）=1-5a-1+a=-4a
启发应用：
（1）按照上面的解法，化简：；
类比迁移：
（2）已知△ABC的三边长分别为，请求出△ABC的周长。（用含有x的代数式表示，结果要求化简）
拓展延伸：
（3）若，请直接写出x的取值范围。
25.在学习了“特殊的平行四边形”这一章后，同学小明对特殊四边形的探究产生了浓厚的兴趣，他发现除了已经学过的特殊四边形外，还有很多比较特殊的四边形，勇于创新的他大胆地作出这样的定义：有一个内角是直角，且对角线互相垂直的四边形称为“双直四边形”.请你根据以上定义，回答下列问题：
（1）下列关于“双直四边形”的说法，正确的有 （把所有正确的序号都填上）；
①双直四边形”的对角线不可能相等：
②“双直四边形”的面积等于对角线乘积的一半；
③若一个“双直四边形”是中心对称图形，则其一定是正方形.
（2）如图①，正方形ABCD中，点E、F分别在边AB、AD上，连接CE，BF，EF，CF，线段BF，CE相交于点 O，若AE=DF，证明：四边形 BCFE为“双直四边形”；
（3）如图②，在平面直角坐标系中，已知点A（0，4），C（8，0），点B在线段OC上，且AB=BC，在第一象限内，是否存在点D，使得四边形ABCD为“双直四边形”，若存在；请直接写出所有点 D 的坐标，若不存在，请说明理由.