




北京市丰台第八中学2023-2024学年八年级下学期期中数学试题(原卷版+解析版)
展开一、选择题(本题共24分,每小题3分)下面各题均有四个选项,符合题意的选项只有一个.
1. 下列四组线段中,能作为直角三角形三条边的是( ).
A. 3,4,6B. 6,8,10C. 1,2,D. 5,12,15
2. 如图,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,并分别找出AC和BC的中点M,N,如果测得MN=20m,那么A,B两点间的距离是多少?()
A 20mB. 30mC. 40mD. 50m
3. 下列式子是最简二次根式的是( ).
A. B. C. D.
4. 下列计算正确的是( )
A. B. C. D.
5. 如图,在平面直角坐标系中,已知点O(0,0),A(2,3),以点O为圆心,OA长为半径画弧,交x轴的正半轴于B点,则B点的横坐标介于( )
A. 3和4之间B. 4和5之间C. 5和6之间D. 6和7之间
6. 如图,在矩形中,对角线,交于点O,若,,则的长为( ).
A. 9B. 3C. D. 6
7. 某学校为了让学生更好地体会中国传统节日的文化内涵,在端午节到来之际,组织“端午诗词朗诵会”、邀请两位学生和两位教师担任评委,比赛评分规则为:每位评委先按十分制对参赛选手独立打分,然后将两位学生评委和两位教师评委的评分按照的比,计算出选手的最终成绩.下表是四位评委给某位选手的打分成绩:
则该选手的最终成绩是( )
A. 分B. 分C. 分D. 分
8. 在平行四边形ABCD中,O为AC的中点,点E,M为AD边上任意两个不重合的动点(不与端点重合),EO的延长线与BC交于点F,MO的延长线与BC交于点N.下面四个推断:①EF=MN;②EN∥MF;③若平行四边形ABCD是菱形,则至少存在一个四边形ENFM是菱形;④对于任意的平行四边形ABCD,可能存在无数个四边形ENFM是矩形,其中,所有正确的有( )
A. ①③B. ②③C. ①④D. ②④
二、填空题(本题共16分,每小题2分)
9. 使二次根式有意义的的取值范围是______.
10. 如图,请给矩形ABCD添加一个条件,使它成为正方形,则此条件可以为________.
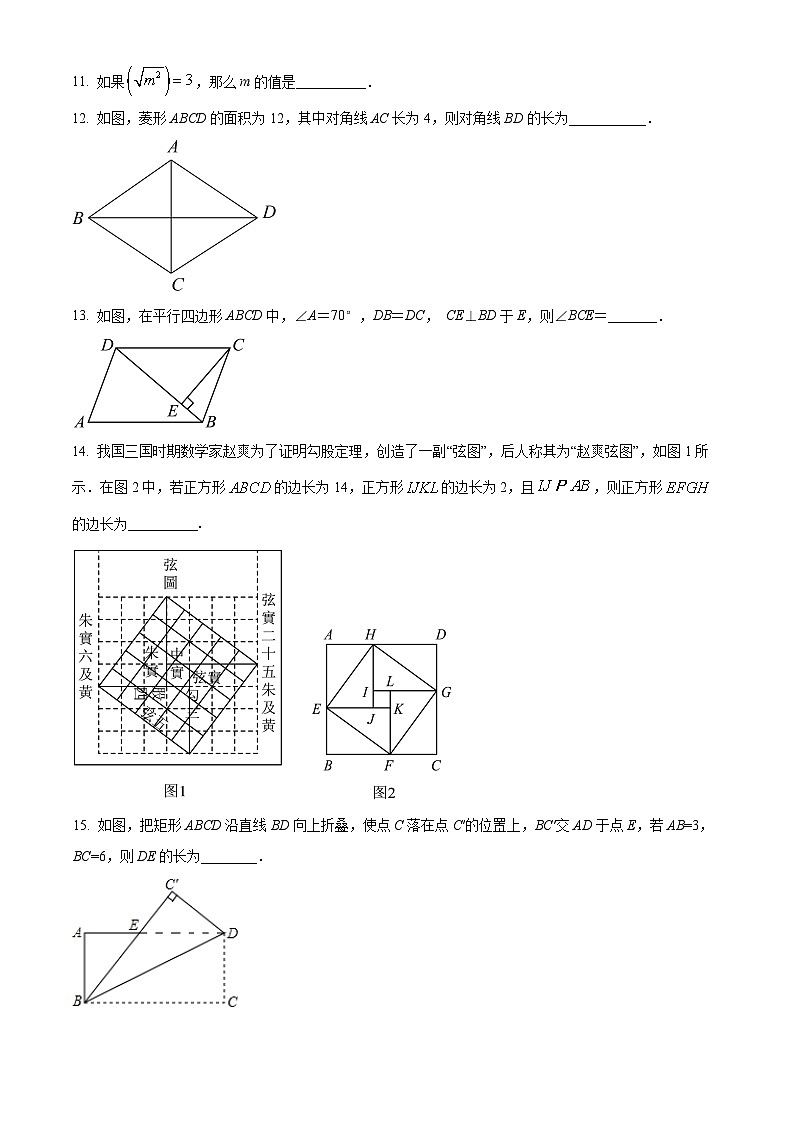
11. 如果,那么m的值是__________.
12. 如图,菱形ABCD的面积为12,其中对角线AC长为4,则对角线BD的长为___________.
13. 如图,在平行四边形ABCD中,∠A=70°,DB=DC, CE⊥BD于E,则∠BCE=_______.
14. 我国三国时期数学家赵爽为了证明勾股定理,创造了一副“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形的边长为14,正方形的边长为2,且,则正方形的边长为__________.
15. 如图,把矩形ABCD沿直线BD向上折叠,使点C落在点C′的位置上,BC′交AD于点E,若AB=3,BC=6,则DE的长为________.
16. 如图,点A、B、C在同一条线上,点B在点A,C之间,点D,E在直线同侧,,,,连接,设,,,给出下面三个结论:
①;②;③.上述结论中,所有正确结论的序号__________.
三、解答题(本题共60分,17~23每题5分,24~26题6分,27题7分)
17. 计算:
18. 计算:.
19. 计算:.
20. 如图所示,已知点在的对角线上,且.求诉:.
21. 下面是小明设计的作菱形的尺规作图过程.
已知:四边形是平行四边形.
求作:菱形(点在上,点在上).
作法:如图,
①以为圆心,长为半径作弧,交于点;
②以为圆心,长为半径作弧,交于点;
③连接,所以四边形为所求的菱形.
(1)根据小明设计的尺规作图过程,使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:
∵,,
∴____________,
在平行四边形中,,
即,
∴四边形为平行四边形,(______)(填推理的依据)
∵,
∴四边形为菱形.(______)(填推理的依据)
22. 某地下车库出口处安装了“两段式栏杆”如图1所示,现需要配一适合该地下车库的车辆限高标志牌,点A是栏杆转动的支点,距离地面的高度约为米,点E是栏杆两段的联结点,距离点A约为米.当车辆经过时,栏杆升起,受现实因素限制,栏杆最多只能升起到如图2所示的水平位置,(栏杆宽度忽略不计),经测量,此时.
要想解决这个问题,小张这样思考:将此问题抽象为数学图形如图3所示,过点E向作垂线,交延长线于点C,计算的长,就可以估计出匹配的限高标志牌(限高值应小于实际高度0.2米).请你结合小张的思路进行计算,并在以下选项中选出适合该地下车库的车辆限高标志.
A. B. C. D.
23. 第24届冬季奥林匹克运动会将于2022年2月4日至2月20日在中国北京和张家口市联合举行.为了解学生对冬奥会冰雪项目的认识程度,某校体育组老师从该校八年级学生中随机抽取了20名学生进行冰上项目和雪上项目的知识测试,获得了他们的测试成绩(百分制),并对数据(测试成绩)进行整理、描述和分析.下面给出了部分信息.
a.测试成绩的频数分布表如下:
b.雪上项目测试成绩在这一组的是:
70,70,70,71,71,73,75
c.冰上项目和雪上项目测试成绩的平均数、中位数、众数如下:
根据以上信息,回答下列问题:
(1)表中的值为__________;
(2)在此次测试中,某学生的冰上项目测试成绩为75分,雪上项目测试成绩为73分,这名学生测试成绩排名更靠前的是_______(填“冰上”或“雪上”)项目,并说明理由;
(3)已知该校八年级共有200名学生,假设该年级学生都参加此次测试,估计冰上项目测试成绩不低于80分的人数.
24. 如图,在中,,D为中点.过点D作的平行线,过点B作的平行线,两平行线相交于点E,交于点F,连接.求证:
(1)四边形矩形;
(2)取的中点M,连接,若,,直接写出矩形的面积.
25. 在数学课上,老师说统计学中常用平均数不是只有算术平均数一种,好学的小聪通过网络搜索,又得到了两种平均数的定义,他把三种平均数的定义整理如下:
对于两个数a,b,
称为a,b这两个数的算术平均数,
称为a,b这两个数的几何平均数,
称为a,b这两个数的平方平均数.
小聪根据上述定义,探究了一些问题,下面是他的探究过程,请你补充完整:
(1)若a = -1,b = -2,则M = ,N = ,P = ;
(2)小聪发现当a,b两数异号时,在实数范围内N没有意义,所以决定只研究当a,b都是正数时这三种平均数的大小关系.结合乘法公式和勾股定理的学习经验,他选择构造几何图形,用面积法解决问题:
如图,画出边长为a+b的正方形和它的两条对角线,则图1中阴影部分的面积可以表示N2.
①请分别在图2,图3中用阴影标出一个面积为M2,P2的图形;
②借助图形可知当a,b都是正数时,M,N,P大小关系是: (把M,N,P从小到大排列,并用“<”或“≤”号连接).
26. 在平面直角坐标系中,对于点A和线段,如果点A,O,M,N按逆时针方向排列构成菱形,且,则称线段是点A的“相关线段”.例如,图1中线段是点A的“-相关线段”.如图2,已知点B的坐标是.
(1)在图2中画出点B的“-相关线段”,并直接写出点M和点N的坐标;
(2)若点B的“相关线段”经过点,求的值.
27. 正方形ABCD中,点M是直线BC上的一个动点(不与点B,C重合),作射线DM,过点B作BN⊥DM于点N,连接CN.
(1)如图1,当点M在BC上时,如果∠CDM=25°,那么∠MBN的度数是 .
(2)如图2,当点M在BC的延长线上时,
①依题意补全图2;
②用等式表示线段NB,NC和ND之间的数量关系,并证明.
学生评委
教师评委
评委
评委
评委
评委
分
分
分
分
冰上项目
0
0
12
6
2
雪上项目
1
4
7
3
5
项目
平均数
中位数
众数
冰上项目
7795
76
75
雪上项目
76.85
70
北京市丰台第八中学2023-2024学年八年级下学期期中数学试题(无答案): 这是一份北京市丰台第八中学2023-2024学年八年级下学期期中数学试题(无答案),共7页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
北京市通州区2023-2024学年八年级下学期期中数学试题(原卷版+解析版): 这是一份北京市通州区2023-2024学年八年级下学期期中数学试题(原卷版+解析版),文件包含北京市通州区2023-2024学年八年级下学期期中数学试题原卷版docx、北京市通州区2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
北京市房山区2023-2024学年八年级下学期期中数学试题(原卷版+解析版): 这是一份北京市房山区2023-2024学年八年级下学期期中数学试题(原卷版+解析版),文件包含北京市房山区2023-2024学年八年级下学期期中数学试题原卷版docx、北京市房山区2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。












