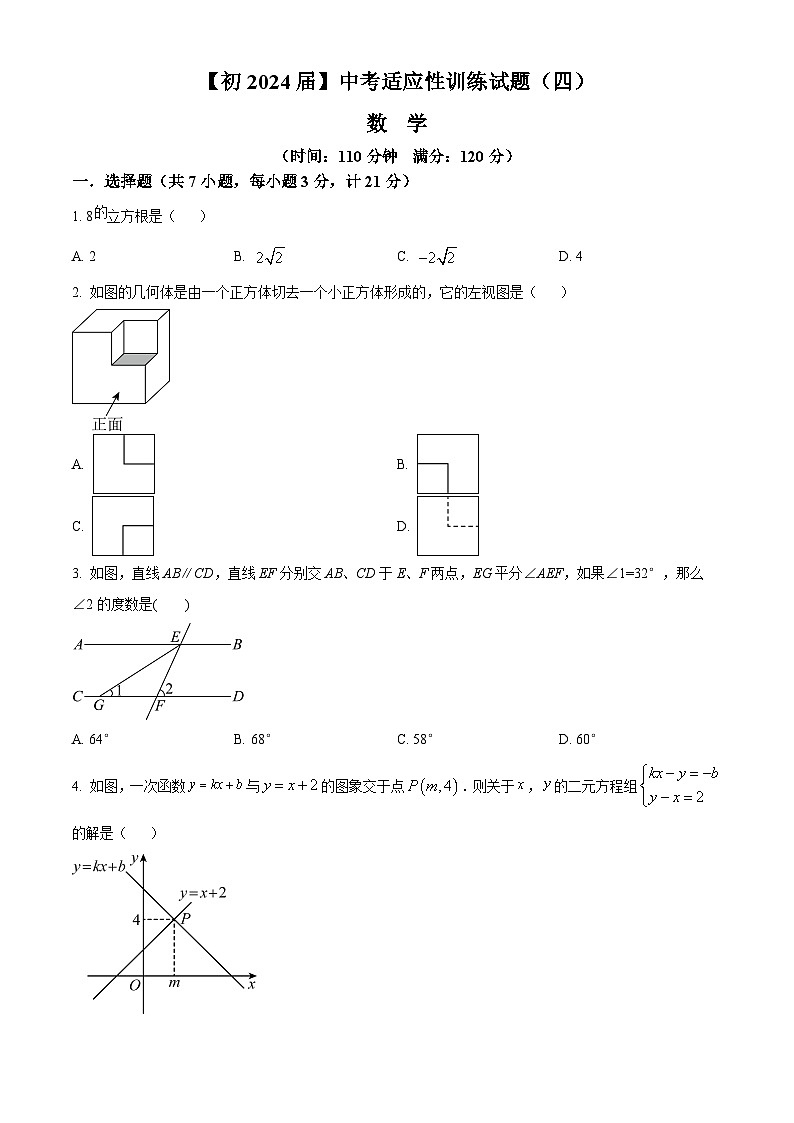




2024年陕西省西安国际港务区铁一中陆港初级中学中考四模数学试题(原卷版+解析版)
展开(时间:110分钟 满分:120分)
一.选择题(共7小题,每小题3分,计21分)
1. 8立方根是( )
A. 2B. C. D. 4
2. 如图的几何体是由一个正方体切去一个小正方体形成的,它的左视图是( )
A. B.
C. D.
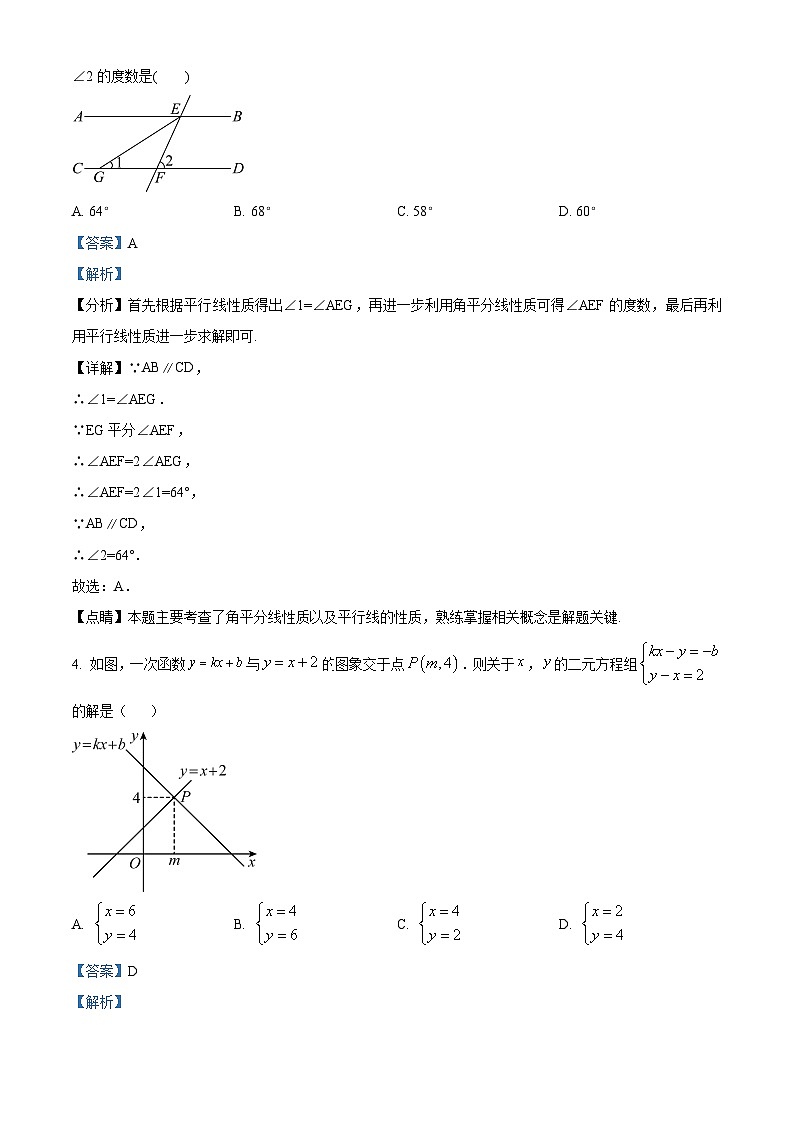
3. 如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF,如果∠1=32°,那么∠2的度数是( )
A. 64°B. 68°C. 58°D. 60°
4. 如图,一次函数与的图象交于点.则关于,的二元方程组的解是( )
A. B. C. D.
5. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标( )
A. (﹣1,﹣1)B. (﹣,﹣1)C. (﹣1,﹣)D. (﹣2,﹣1)
6. 如图,是半圆的直径,点是弧的中点,若.则等于( )
A B. C. D.
7. 已知二次函数的图象开口向上,且经过点,.当二次函数在时,的最大值为1.则的值为( )
A. B. C. D.
二.填空题(共6小题,每小题3分,计18分)
8. 数轴上的点A表示的数是1,将点A向左平移7个单位长度到达点B,则点B表示的数是________.
9. 为实现我国2030年前碳达峰、2060年前碳中和的目标,光伏发电等可再生能源将发挥重要作用.去年全国光伏发电量为3259亿千瓦时,数据“3259亿”用科学记数法表示为________.
10. 已知正六边形的边心距为,则它的外接圆半径为______.
11. 如图,在矩形中,是边的中点,连接交对角线于点,若,,则的长为________.
12. 如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,,以AB为边向上作正方形ABCD.若图像经过点C的反比例函数的解析式是,则图像经过点D的反比例函数的解析式是______.
13. 如图,在边长为8的菱形中,,为上方一点,且,则周长的最小值为______.
三.解答题(共13小题,计81分,解答应写出过程)
14. 计算:
15. 求不等式正整数解.
16. 先化简,再求值:,其中.
17. 点P是外部一个点,过点P作直线(要求用尺规作图,保留作图痕迹,不写做法)
18. 如图,已知,,点、在线段上,与交于点,且,.求证:是等腰三角形.
19. 我国古代名著《张邱建算经》中记载:“今有清酒一斗直粟八斗,醐酒一斗直粟二斗,今持粟两斛,问清、醐酒各几何?”大意:现在一斗清酒价值8斗谷子,一斗醐酒价值2斗谷子,拿20斗谷子共换了4斗酒,问清酒、醐酒各几斗?
20. 秦腔,别称“梆子腔”,中国汉族最古老的戏剧之一,起于西周,源于西府,成熟于秦,是华夏民族文化的瑰宝,它深刻诠释了汉文化的发展,同时也承载着广大西部地区人民的精神寄托,是人们互相交流情感的一种方式.李爷爷,刘爷爷两位秦腔爱好者都想参加中老年俱乐部的汇演活动,需要各自从下面四部曲目中分别随机选择一部进行表演,如图所示,卡片除正面图案不同外,其余均相同.卡片洗匀后,背面朝上放置在桌面上.
(1)李爷爷从中随机抽取一张,卡片正面是“D.龙凤呈祥”的概率是______;
(2)若李爷爷先从这4张卡片中随机抽取一张,不放回,刘爷爷再从剩下的3张卡片中随机抽取一张,请用画树状图或列表的方法,求两人中有一个人抽中“A.周仁回府”这个曲目的概率.
21. 每到三月就会让人想起那句:“西湖美景,三月天哪”,雷峰塔是杭州西湖的标志性景点,为了测出雷峰塔的高度,初三学生小白设计出了下面的测量方法:已知塔前有一米高的小树,发现水平地面上点、树顶和塔顶恰好在一条直线上,测得米,之间有一个花圃无法测量,然后在处放置一个平面镜,沿后退.退到处恰好在平面中看到树顶的像,此时米,测量者眼睛到地面的距离为米,求出塔高.
22. 港务区苗木种植专业户老王承包了亩地,分别种植柏树苗和松树苗,有关成本、销售额见下表:
设种植柏树苗亩,出售柏树苗和松树苗的总利润为万元.
(1)求与的函数表达式;
(2)今年,他继续用这亩地全部种柏树苗和松树苗,计划投入成本不超过万元,若每亩的种植成本和销售额不变.他应如何安排种植才能获得最大收益?最大收益为多少?(收益销售额成本)
23. 【问题情境】数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动.
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长(单位:),宽(单位:)的数据后,分别计算长宽比,整理数据如下:
【实践探究】分析数据如下:
【问题解决】
(1)上述表格中:______,______;
(2)①同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”
②同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.”
上面两位同学的说法中,合理的是______(填序号);
(3)现有一片长,宽的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并说明理由.
24. 如图,为的直径,点为圆周上一点,的延长线交的切线于点的延长线交的切线于点.
(1)求证:;
(2)若,求的长.
25. 在行知学校第二届趣味篮球赛活动中,某班一位身高女同学参加定点投篮比赛(如图①).为了获得更好的成绩,同学们对这位选手的训练数据进行了收集和分析:篮球运行的路线是一条抛物线,不起跳投掷时,球在该选手头顶上方处投出,在距离该选手时达到最大高度.
(1)如图②,以该选手投球站立点为原点、身体竖直向上方向为轴正半轴建立平面直角坐标系,求出篮球运行高度与运行水平距离之间函数关系式;
(2)已知比赛时篮圈中心到地面高度为,为保证篮球准确投入篮圈内,该选手在训练时应如何调整自己的起跳高度?
26. 综合运用
如图1,在平面直角坐标系中,正方形的顶点A在轴的正半轴上,如图2,将正方形绕点逆时针旋转,旋转角为,交直线于点,交轴于点.
(1)当旋转角为多少度时,;(直接写出结果,不要求写解答过程)
(2)若点,求的长;
(3)如图3,对角线交轴于点,交直线于点,连接,将与的面积分别记为与,设,,求关于的函数表达式.种植种类
成本(万元/亩)
销售额(万元/亩)
柏树苗
松树苗
1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
荔枝树叶的长宽比
2.0
平均数
中位数
众数
方差
芒果树叶的长宽比
荔枝树叶的长宽比
2024年陕西省西安国际港务区铁一中陆港初级中学中考四模数学试卷: 这是一份2024年陕西省西安国际港务区铁一中陆港初级中学中考四模数学试卷,共4页。
2024年陕西省西安国际港务区铁一中陆港初级中学中考二模数学试题(无答案): 这是一份2024年陕西省西安国际港务区铁一中陆港初级中学中考二模数学试题(无答案),共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
56,2024年陕西省西安市国际港务区铁一中陆港初级中学中考一模数学试题: 这是一份56,2024年陕西省西安市国际港务区铁一中陆港初级中学中考一模数学试题,共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












