







模拟卷01-【赢在中考·黄金8卷】备战2024年中考数学模拟卷(江苏宿迁专用)
展开1、锻炼学生的心态。能够帮助同学们树立良好的心态,增加自己的自信心。
2、锻炼学生管理时间。通过模拟考试就会让同学们学会分配时间,学会取舍。
3、熟悉题型和考场。模拟考试是很接近中考的,让同学们提前感受到考场的气氛和布局。
中考的取胜除了平时必要的学习外,还要有一定的答题技巧和良好心态。此外,通过模拟考试还能增强学生们面对高考的信心,希望考生们能够重视模拟考试。
【赢在中考·黄金8卷】备战2024年中考数学模拟卷(宿迁专用)
黄金卷01
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答填空题时,请将每小题的答案直接填写在答题卡中对应横线上。写在本试卷上无效。
4.回答解答题时,每题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上。写在本试卷上无效。
5.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题3分,共24分。
1.若,则的值为( )
A.B.C.D.
【答案】B
【分析】本题考查比例的性质,解题的关键是学会利用参数解决问题.设,,,代入求解即可.
【详解】解:,
可以假设,,
.
故选:B.
2.如图,,,与的面积分别是与,周长分别是与,则下列说法正确的是( )
A.B.C.D.
【答案】A
【分析】本题考查了相似三角形的性质,根据相似三角形的性质判断即可,熟练掌握相似三角形的性质定理是解题的关键.
【详解】解:,,
,故A正确;
,故B错误;
,故C错误;
,故D错误;
故选:A.
3.如图,在中,,.以为圆心,为半径的交于点.点在上,连接,,若,则的半径为( )
A.1B.C.2D.
【答案】B
【分析】本题考查了解直角三角形,圆周角定理,根据圆周角定理得出,进而得出,再根据,即可求解.
【详解】解:,
,
,
,
,
,
,
故选:B.
4.二次函数的图象与x轴有交点,则k的取值范围是( )
A.B.且C.D.且
【答案】D
【分析】本题考查了抛物线与轴的交点:对于二次函数(是常数,),决定抛物线与轴的交点个数:时,抛物线与轴有2个交点;时,抛物线与轴有1个交点;时,抛物线与轴没有交点.根据二次函数的定义得到,根据决定抛物线与轴的交点个数可得到,然后求出两不等式的公共部分即可.
【详解】解:∵二次函数的图象与轴有交点,
∴且,
∴且.
故选:D.
5.学校通过以下方式抽取部分同学免费参加活动:在一个装有6个红球和若干白球(每个球除颜色外,其它都相同)的袋中,随机摸一个球,摸到一个红球就得“民间美术展”活动门票一张,已知参加抽取活动的同学共有人,“民间美术展”活动门票张,则白球的数量是( )
A.个B.个C.个D.个
【答案】D
【分析】本题主要考查了利用频率估计概率,根据概率求数量;设袋中共有个白球,根据摸到红球的概率求出球的总个数,即可解答.
【详解】解:设袋中共有个白球,则摸到红球的概率为,
∴,
解得,经检验:时,,
所以是原方程的解.
故选:D.
6.“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以等边三角形ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”.若等边三角形的边长为2,则该“莱洛三角形”的面积等于( )
A.B.C.D.
【答案】C
【分析】本题考查了不规则图形的面积的求解,能够得出“莱洛三角形的面积为三个扇形的面积相加,再减去两个等边三角形的面积”是解题的关键.莱洛三角形的面积为三个扇形的面积相加,再减去两个等边三角形的面积,代入已知数据计算即可.
【详解】解:如图所示,作交于点D,
∵是等边三角形,
∴,,
∵,
∴,,
∴,
∴莱洛三角形的面积为
故选:C.
7.某医疗公司计划在两个月内将一种测温仪器的销售单价调低19%,则平均每月应调低( )
A.9%B.9.5%C.10%D.11%
【答案】C
【分析】本题考查了一元二次方程的实际应用——增长率问题,根据题意列出方程并求解即可,熟练增长率和解一元二次方程是解题的关键.
【详解】设平均每月应调低
由题意得
解得或(舍去)
故选:.
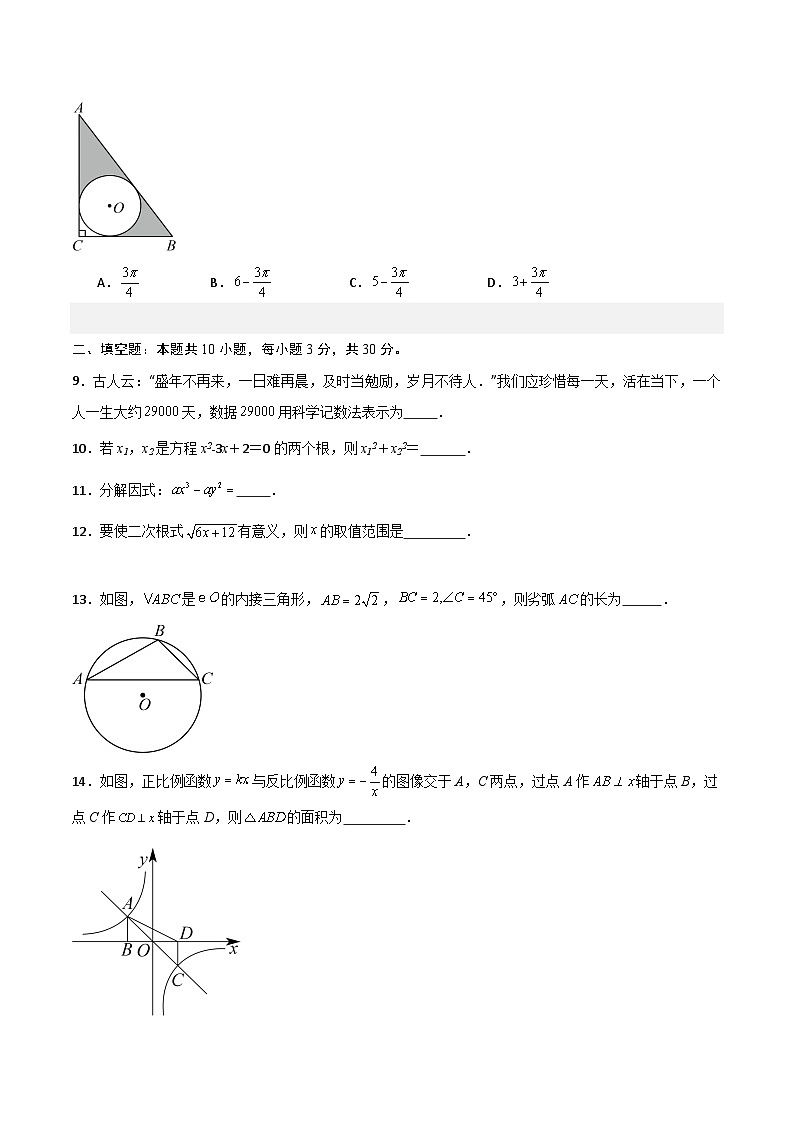
8.如图,在中,,,,为的内切圆,则图中阴影部分的面积为(结果保留)( )
A.B.C.D.
【答案】C
【分析】本题考查了三角形内切圆的性质;勾股定理求得,进而根据等面积法求得,三角形的内切半径,根据,即可求解.
【详解】解:中,,,
,
,,
内切圆半径,
,
设与切于点,与切于点,连接、,
则四边形为正方形,
.
故选:C.
二、填空题:本题共10小题,每小题3分,共30分。
9.古人云:“盛年不再来,一日难再晨,及时当勉励,岁月不待人.”我们应珍惜每一天,活在当下,一个人一生大约天,数据用科学记数法表示为 .
【答案】
【分析】本题考查了绝对值大于1的科学记数法的表示,解题的关键在于确定的值.
根据绝对值大于1的数,用科学记数法表示为,其中,的值为整数位数少1.
【详解】解:大于1,用科学记数法表示为,其中,,
∴用科学记数法表示为,
故答案为:.
10.若x1,x2是方程x2﹣3x+2=0的两个根,则x12+x22= .
【答案】5
【分析】根据根与系数的关系得到x1+x2=3,x1•x2=2,把x12+x22变形得到(x1+x2)2﹣2x1x2然后利用整体代入的方法计算.
【详解】解:根据题意得x1+x2=3,x1•x2=2,
则x12+x22=(x1+x2)2﹣2x1x2=9﹣4=5,
故答案为:5.
【点睛】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则,.
11.分解因式: .
【答案】/
【分析】本题考查提公因式法分解因式,提取公因式a进行因式分解即可.
【详解】解:原式=,
故答案为:.
12.要使二次根式有意义,则的取值范围是 .
【答案】/
【分析】本题主要考查了二次根式有意义的条件以及解一元一次不等式,理解二次根式有意义的条件是解题关键.二次根式有意义的条件,即被开方数大于等于0,根据二次根式有意义的条件列出不等式,解不等式即可.
【详解】解:要使二次根式有意义,
则有,
解得,
所以,的取值范围是.
故答案为:.
13.如图,是的内接三角形,,,则劣弧的长为 .
【答案】
【分析】本题考查了圆周角定理,弧长公式,等边三角形的判定和性质,勾股定理,连接,先关键圆周角定理得出,再利用勾股定理求出,继而证明是等边三角形,即可得出,最后利用弧长公式计算即可.
【详解】连接,
∵,
∴,
∵,
∴,
∵,
∴是等边三角形,
∴,
∴,
∴劣弧的长为,
故答案为:.
14.如图,正比例函数与反比例函数的图像交于A,C两点,过点A作轴于点B,过点C作轴于点D,则的面积为 .
【答案】4
【分析】根据反比例函数的k的几何意义,可得,根据反比例函数与正比例函数的中心对称性,可知O是的中点,即可得到答案;
【详解】解:∵点A在反比例函数,轴,
∴,
∵正比例函数与反比例函数的图像交于A,C两点,轴,
∴O是的中点,
∴,
故答案为4.
【点睛】本题考查了反比例函数的性质,熟练掌握反比例函数k的几何意义和中心对称性是解题的关键..
15.如图,和是等腰直角三角形,,的边AF,AG交边BC于点D,E.若,,则AD的值是 .
【答案】
【分析】本题考查了旋转全等和勾股定理解三角形,将顺时针旋转到位置,得到直角三角形,可求出,再证明,得到,进而求出,过点A作,由等腰三角形三线合一和直角三角形斜边中线等于斜边一半得出,再在直角三角形求出.
【详解】解:如图,将绕点A顺时针旋转到位置,连接
∵和是等腰直角三角形,,
∴,,
由旋转性质可知:,,,
∴,
∴,
∵,,
∴,
∴,
又∵,,
∴,
∴,
∴,
过点A作,
∵,,
∴,
∴,
∴,
故答案为.
【点睛】本题涉及了旋转的性质、半角模型、构造全等三角形转换线段关系和勾股定理,解题关键是通过旋转构造全等三角形得到,由求出.
16.如图,在中,,,边,分别交于点D,E,连接,则的度数为 .
【答案】/80度
【分析】本题考查了已知圆内接四边形求角度,三角形外角性质,根据是圆的内接四边形求出的度数,利用三角形外角性质即可求出结果.
【详解】解:四边形内接于,
,
,
,
,
,
故答案为:.
17.设的整数部分,小数部分为,则 .
【答案】
【分析】本题考查了无理数的整数部分和小数部分,以及估算无理数大小,先把式子分母有理化,再估算出所在范围,再根据化简后的式子进行变形,即可解题.
【详解】解:,
,
,
,
,
的整数部分,小数部分为,
,.
故答案为:.
18.如图,矩形的对角线相交于点O,,,点在对角线上,P是的中点,的最小值是 .
【答案】
【分析】此题重点考查矩形的性质、轴对称的性质、等边三角形的判定与性质、三角形的中位线定理、直角三角形中30°角所对的直角边等于斜边的一半、勾股定理、两点之间线段最短等知识,正确地作出所需要的辅助线是解题的关键.取的中点F,再作B关于的对称点H,与交于点G,连接,求出,再利用三角形的三边关系可得答案.
【详解】解:取的中点F,作直线,
∵点P是的中点,
∴,
∴,
作点B关于直线的对称点H,连接交直线于点G,连接,
∵垂直平分,
∴,,
∵四边形是矩形,,
∴,,,,
∴,
∵,
∴,
∴是等边三角形,
∴,,
∴,,
∴,
∴,
∴,
∴,
∵,
∴,
∴PO+PB的最小值为,
故答案为:.
三、解答题:本题共10小题,共96分。
19.(本题8分)
(1)计算;
(2)解不等式组.
【答案】(1);(2).
【分析】(1)根据算术平方根性质、绝对值性质、负整数指数幂的运算法则化简,再运用有理数的加减法则运算;
(2)分别求解组中的不等式,取公共部分得不等式组解集.
【详解】解:(1)原式;
(2),
解不等式①得,,
解不等式②得,,
∴不等式组的解集为.
【点睛】本题考查有理数的运算,不等式组的求解;掌握相关运算法则是解题的关键.
20.(本题8分)按要求解下列方程
(1)(配方法);
(2)(公式法).
【答案】(1);
(2).
【分析】本题考查了解一元二次方程:
(1)先把常数项移到等号的右边,再等号左右两边同时加上一次项系数的一半的平方,配成完全平方公式,即可作答.
(2)先找出,再结合公式代入数值化简,即可作答.
【详解】(1)解:
或
;
(2)解:
∴方程有两个不相等的实数根
.
21.(本题12分)文明是一座城市的名片.某校积极组织师生参加全县“共创文明城市,巩固国家卫生县城”志愿者服务活动,其服务项目有“清洁卫生”“敬老服务”“文明宣传”“交通劝导”,每名志愿者只参加其中一项服务活动.为了解各项目参与情况,该校随机调查了参加志愿服务的部分师生,将调查结果绘制了如下不完整的统计图.
(1)本次调查采用的调查方式为______(填写“普查”或“抽样调查”);
(2)本次调查的师生共有______人,扇形统计图中n的值为______;
(3)已知参加交通劝导志愿者服务活动30名师生中,有10名教师和20名学生,若从这30名师生中随机抽取1名志愿者参加“共创文明城市,巩固国家卫生县城”主题演讲比赛活动,且每名志愿者被抽到的可能性相同,恰好抽到学生的概率是______;
(4)若该校共有师生3000名,请估计有______人参加“文明宣传”志愿者服务活动.
【答案】(1)抽样调查
(2)300,40
(3)
(4)900
【分析】本题考查条形统计图和扇形统计图的关联、简单的概率计算、用样本估计总体,理解题意,看懂统计图是解答的关键.
(1)根据调查方式的特点求解即可;
(2)用参加“清洁卫生”人数除以其所占的百分比可求解调查人数,再由参加“敬老服务”人数除以调查总人数可求得n值;
(3)用参加“交通劝导”中学生人数除以参加“交通劝导”总人数即可求得抽到学生的概率;
(4)用总人数乘以样本中参加“文明宣传”志愿者服务活动的百分比即可求解.
【详解】(1)解:本次调查采用的调查方式为抽样调查,
故答案为:抽样调查;
(2)解:本次调查的师生共有(人),,
故答案为:300,40;
(3)解:从有10名教师和20名学生中随机抽取1名志愿者参加“共创文明城市,巩固国家卫生县城”主题演讲比赛活动,且每名志愿者被抽到的可能性相同,恰好抽到学生的概率是,
故答案为:;
(4)解:∵参加“文明宣传”志愿者服务活动人数为(人),
∴该校共有师生3000名,估计有人参加“文明宣传”志愿者服务活动.
22.(本题8分)一个仅装有球的不透明布袋里共有3个球(只有颜色不同),其中1个红球,2个白球.从中任意摸出1个球,记下颜色后放回,搅匀,再摸出1个球.求:
(1)摸出的2个球都是白球的概率.
(2)摸出的2个球中,1个是白球,1个是红球的概率.
【答案】(1)
(2)
【分析】本题考查树状图法或列表法求概率,正确画出树状图得到所有可能结果是解答的关键.
(1)从树状图中找出摸出的2个球都是白球的结果数,再利用概率公式求解即可;
(2)从树状图中找出摸出1个是白球,1个是红球的结果数,再利用概率公式求解即可;
【详解】(1)解:画树状图如下:
共有9种等可能的结果,其中摸出的2个球都是白球的结果有4种,
∴摸出的2个球都是白球的概率为.
(2)解:由树状图可知,摸出的2个球中,1个是白球,1个是红球的结果有4种,
∴摸出的2个球中,1个是白球,1个是红球的概率为.
23.(本题8分)在中,已知,求的长.
【答案】
【分析】本题考查解直角三角形、特殊角的三角函数值.先作于点D,根据直角三角形的性质和锐角三角形函数,即可得到,,进而得出答案.
【详解】解:作于点D,如图,
∵,
∴,,,
∴.
24.(本题8分)已知二次函数解析式为.
(1)请将函数的表达式用配方法化为的形式;
(2)请写出函数图象的顶点坐标与对称轴.
【答案】(1)
(2)顶点坐标为,对称轴为直线
【分析】本题考查了待定系数法,掌握配方法是解题的关键.
(1)根据配方法求解;
(2)根据抛物线的顶点式求解.
【详解】(1)解:(1)
;
(2)图象的顶点坐标为,对称轴为直线.
25.(本题8分)如图,学校课外兴趣活动小组准备利用长为的墙和一段长为的篱笆围建一个矩形苗圃园.如果矩形苗圃园的一边由墙和一节篱笆构成,另三边由篱笆围成,设平行于墙一边长为.
(1)当苗圃园的面积为时,求的值.
(2)当为何值时,所围苗圃园的面积最大?最大面积是多少?
【答案】(1)
(2)当的值为8.5m时,所围苗圃园的面积最大,最大面积是
【分析】本题考查列代数式,一元二次方程的应用,二次函数的最值问题,
(1)用含的式子表示,根据“苗圃园的面积为”列出关于的方程,求解即可;
(2)设苗圃园的面积为,根据面积公式可得到二次函数,通过二次函数的性质即可求出最值;
本题的关键是利用含x的式子表示线段长度,根据二次函数的性质解题.
【详解】(1)解:∵篱笆的总长为,平行于墙一边长为,
∴垂直于墙一边长为,
根据题意得:,
解得:(不符合题意,舍去),,
∴的值为;
(2)设苗圃园的面积为,
依题意,得:,
∴,
∴当时,,
答:当的值为8.5m时,所围苗圃园的面积最大,最大面积是.
26.(本题10分)如图,延长矩形的边到点,使,连接,是上一点,连接交于点,交于点.
(1)求证:;
(2)若,,,求的长.
【答案】(1)证明见解析
(2)
【分析】本题考查平行四边形的性质,矩形的性质,相似三角形的性质和判定,平行线分线段成比例性质等知识,掌握相似三角形的性质和判定是解本题的关键.
(1)先根据四边形是矩形,可得,再得出,由四边形是平行四边形,可得,再由平行线分线段成比例定理可得最后可得结论;
(2)由平行线性质可得,再由直角三角形性质可得,再证明,再由相似三角形的性质可得,求得,最后可得结果.
【详解】(1)四边形是矩形,
.
,
四边形是平行四边形,
,
.
(2)
,
.
.
,
,
即
,
.
27.(本题12分)如图,已知四边形是矩形,把沿对角线翻折得到,交于点,是的外接圆.
(1)利用尺规作出的外接圆(要求保留作图痕迹,不写作法);
(2)求证:;
(3)若,试判断与直线的位置关系,并说明理由.
【答案】(1)见解析;
(2)见解析;
(3)直线是的切线,理由见解析
【分析】此题是圆的综合题,主要考查了尺规作图,矩形的性质,等腰三角形的判定和性质,等边三角形的判定,锐角三角函数,求出是解本题的关键.
(1)先作出,的垂直平分线,找出圆心,即可得出结论;
(2)先判断出,即可得出结论;
(3)先求出,进而依次求出,,,再判断出,进而求出,判断出是等边三角形,即可得出结论.
【详解】(1)解:如图,为所求作的图形.
(2)证明:∵四边形是矩形,
∴,
∴,
由折叠知,,
∴,
∴.
(3)解:直线是的切线,
如图,连接,,
∵四边形是矩形,
∴,,
∵,
∴,
在中,,
∴,
∴,
由折叠知,,
∴,
∴,
由折叠知,,
∴,
∴,
由(2)知,,
∴,
∴,
∵,
∴是等边三角形,
∴,
∴,
∴,
∵点在上,
∴直线是的切线.
28.(本题14分)如图,点、在反比例函数的图象上,点坐标为,连接.
(1)求直线的函数解析式;
(2)①点在直线上运动,当的长最小时,求点的坐标;
②______.
【答案】(1);
(2)①;②.
【分析】本题是反比例函数的综合题,考查了待定系数法求一次函数的解析式,勾股定理,三角函数的定义,正确地求出函数的解析式是解题的关键.
(1)根据已知条件列方程,求得、,设直线的函数解析式为,解方程组即可得到结论;
(2)过点作于点,则的长最小,由于点在直线上,可设,求得直线与轴的交点的坐标为,当时,,根据勾股定理得到即可得到结论;
根据两点间的距离公式得到根据三角函数的定义即可得到结论.
【详解】(1)解:点、在反比例函数的图象上,
,,
,
、,
设直线的函数解析式为:,
,
解得,
直线的函数解析式为:;
(2)解:过点作于点,则的长最小,
由于点在直线上,
可设,
由,当时,,
直线与轴的交点的坐标为,
当时,,
直线与轴的交点的坐标为,
,
,
,
,
,
,
,
,,
点的坐标为;
、,
.
在中,.
故答案为:.
模拟卷01-【赢在中考·黄金8卷】备战2024年中考数学模拟卷(安徽专用): 这是一份模拟卷01-【赢在中考·黄金8卷】备战2024年中考数学模拟卷(安徽专用),文件包含黄金卷01安徽专用解析版docx、黄金卷01安徽专用参考答案docx、黄金卷01安徽专用考试版docx等3份试卷配套教学资源,其中试卷共46页, 欢迎下载使用。
模拟卷01-【赢在中考·黄金8卷】备战2024年中考数学模拟卷(浙江新中考专用): 这是一份模拟卷01-【赢在中考·黄金8卷】备战2024年中考数学模拟卷(浙江新中考专用),文件包含黄金卷01解析版docx、黄金卷01参考答案docx、黄金卷01考试版docx等3份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。
模拟卷01-【赢在中考·黄金8卷】备战2024年中考数学模拟卷(深圳专用): 这是一份模拟卷01-【赢在中考·黄金8卷】备战2024年中考数学模拟卷(深圳专用),文件包含黄金卷01解析版docx、黄金卷01参考答案docx、黄金卷01考试版docx等3份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。












