模拟卷04-【赢在中考•黄金8卷】备战2024年中考数学模拟卷（全国通用）

这是一份模拟卷04-【赢在中考•黄金8卷】备战2024年中考数学模拟卷（全国通用），文件包含黄金卷04全国通用解析版docx、黄金卷04全国通用参考答案docx、黄金卷04全国通用考试版docx等3份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。

1、锻炼学生的心态。能够帮助同学们树立良好的心态，增加自己的自信心。
2、锻炼学生管理时间。通过模拟考试就会让同学们学会分配时间，学会取舍。
3、熟悉题型和考场。模拟考试是很接近中考的，让同学们提前感受到考场的气氛和布局。
中考的取胜除了平时必要的学习外，还要有一定的答题技巧和良好心态。此外，通过模拟考试还能增强学生们面对高考的信心，希望考生们能够重视模拟考试。
【赢在中考·黄金8卷】备战2024年中考数学模拟卷（全国通用）
黄金卷04
（考试时间：120分钟 试卷满分：120分）
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。
3．回答填空题时，请将每小题的答案直接填写在答题卡中对应横线上。写在本试卷上无效。
4．回答解答题时，每题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上。写在本试卷上无效。
5．考试结束后，将本试卷和答题卡一并交回。
一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）
1．下列各数中，是负数的是（ ）
A．B．C．D．
【答案】B
【解析】解：A、，是正数，不符合题意；
B、，是负数，符合题意；
C、，是正数，不符合题意；
D、，是正数，不符合题意；
故选：B．
2．打陀螺是北方人们比较喜爱的一种游戏，图中是一款陀螺的示意图，其俯视图为（ ）
A．B．C．D．
【答案】C
【解析】解：该几何体的俯视图如图，
．
故选：C．
3．某校九年级1班10名同学在“二十大知识”竞赛中的成绩如表所示：88，90，75，88，90，91，92，100，80，88则这个班学生成绩的众数、中位数分别是（ ）
A．88，90B．3，C．90，89D．88，89
【答案】D
【解析】这个班学生成绩的众数是：88，
中位数；75，80，88，88， 88，90，90，91，92，100，
，
故选：D．
4．如图，点，，以为边作正方形，点E是边上一点，且，则点E的坐标为（ ）
A．B．C．D．
【答案】A
【解析】解：过点E作于点H，
∵点，，
∴，
∵四边形是正方形，
∴，，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
∴,
∴点E的坐标为，
故选：A
5．如图，某园林公司计划将一块长200m、宽80m的矩形荒地改造成绿色公园，公园内部修建四条宽度相等的石板路，余下区域（阴影部分）种植植被．若要使种植植被区域的面积占整个公园总面积的90%，求小路的宽．设小路的宽为，则可列方程为（ ）
A．B．
C．D．
【答案】A
【解析】解：设小路的宽为x米，则种植植被区域的面积相当于长为米，宽为米的矩形面积，
∴，
故选：A．
6．抛物线的对称轴为直线，给出下列结论：①；②；③；④；⑤．其中正确的个数有（ ）

A．2个B．3个C．4个D．5个
【答案】A
【解析】解：∵抛物线开口向下，与轴的交点在正半轴上，
∴，
∴；故①错误；
∵抛物线与轴由2个交点，
∴，故②正确；
∵对称轴为，
∴，
∴，故③错误；
∵抛物线过点，关于对称轴的对称点为：，
∴；故④正确；
由图象可知：当时，函数值小于时的函数值0，
即：，故⑤错误；
综上，正确的有2个，
故选A．
7．如图，两个反比例函数和（其中）在第一象限内的图象依次是和，设点在上，轴于点，交于点，轴于点，交于点，则四边形的面积为（ ）

A．B．k1−k2C．D．
【答案】B
【解析】根据题意可得四边形PAOB的面积＝S矩形OCPD−S△OBD−S△OAC，
由反比例函数y＝中k的几何意义，可知其面积为k1−k2．
故选B．
8．如图，将边长为4，锐角为的菱形沿折叠，使顶点恰好落在边的中点处，记为，则的长度为（ ）
A．B．C．3D．
【答案】B
【解析】解：如图，过作于点，
，
边长为4，锐角为的菱形，
，，，
，
是的中点，
，
，
，
，，
点与重合，
，，
由折叠的性质得：，
设，
则，
在中，由勾股定理得：，
即，
解得：，
，
故选：B．
9．如图，扇形中，，点为的中点，将扇形绕点顺时针旋转，点的对应点为，连接，当时，阴影部分的面积为( )
A．B． C． D．
【答案】D
【解析】解：如图，连接，
∵，
∴，
∵是的中点，
∴，
∴是等边三角形，
∴，
∴，
∴三点共线，
∴阴影部分的面积为，
故选：D．
10．如图，在平面直角坐标系中，直线l：与坐标轴分别交于A，B两点，点C在x轴正半轴上，且．点P为线段（不含端点）上一动点，将线段绕点O顺时针旋转得线段，连接，则线段的最小值为（ ）
A．B．C．D．
【答案】A
【解析】解：如图，过点P作轴，过点Q作轴，
即，
直线l：与坐标轴交于A、B两点，
，，
由旋转可知：，，
，
，
在和中，
，
，
，，
设，．
点中，．
，即，
点是直线上的点，
记直线与x轴交与点N，
则，，
，
根据垂线段最短可知当时，的长最短，
，
，
，
，
，
，，
，
．
故选：A．
二、填空题（本大题共7小题，每小题4分，共28分）
11．代数式﹣9m2+4n2分解因式的结果是 ．
【答案】
【解析】解：﹣9m2+4n2，
＝（2n）2﹣（3m）2，
＝（2n+3m）（2n﹣3m）．
故答案为：．
12．分式方程的解为 ．
【答案】
【解析】解：去分母得：3x+6＝5x+5，
解得：x＝，
经检验x＝是分式方程的解．
故答案为．
13．现有四张形状、大小、质地均相同的卡片，上面分别标有数字1，2，3，4．从中随机抽取一张卡片，那么抽取的卡片上的数字不大于2的概率是 ．
【答案】/
【解析】解：共有4种情况，摸出的卡片的数字不大于2的有2种，
∴摸出的卡片的数字不大于2的概率为：，
故答案为：．
14．如图，在平行四边形中，点E在边上，连接并延长至点F，使，连接并延长至点G，使，连接若，，则的度数为
【答案】
【解析】解：四边形是平行四边形，
，，
，，
，
，，
是是中位线，
，
故答案为：
15．如图，我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，若小正方形和大正方形的面积分别为49和289，则图中直角三角形内切圆的半径为 ．
【答案】3
【解析】解：如图，设内切圆的圆心为O，连接、，
，
则四边形为正方形，
设直角三角形内切圆的半径为r，
，
，
，
，
，
而，
①，
小正方形和大正方形的面积分别为49和289，
，，
②，负值舍去，
把代入①得，③，
把③代入②中，得：
，
，
负值舍去，
直角三角形内切圆的半径为3，
故答案为：
16．如图，是的直径，，，点为弧的中点，点是直径上的一个动点，则的最小值为 ．

【答案】4
【解析】解：作点B关于直径的对称点E，连接，根据两点之间线段最短及轴对称的性质可得即为的最小值，如图所示：

∴，
∵，
∴，
∵点为弧的中点，
∴与的度数为20°，
∴，
∴，
∵，
∴是等边三角形，
∵，
∴，
即的最小值为4，
故答案为：4．
17．如图，正方形ABCD中，，点E在CD边上，且．将沿AE对折至，延长EF交边BC于点G，连结AG、CF．则 ， ．
【答案】45°；
【解析】解：∵正方形ABCD
∴CD=BC =AB=6，∠D=∠B =∠BAD=∠BCD=90°，
∵CD=3DE，∴DE=2，EC=4，
∵将△ADE沿AE对折至△AFE，
∴AD=AF=AB，DE=EF=2，∠D=∠AFE=90°，∠DAE=∠FAE，
在Rt△ABG和Rt△AFG中，
，
∴Rt△ABG≌Rt△AFG（HL），
∴∠BAG=∠GAF，BG=GF，∠AGB=∠AGE，
∴∠GAF+∠FAE=∠BAG+∠DAE，即∠EAG=∠BAG+∠DAE，
∵∠EAG+∠BAG+∠DAE=∠BAD=90°，
∴∠EAG=45°，
∵GE2=EC2+GC2，
∴（BG+2）2=16+（6-BG）2，
∴BG=3，
∴CG=BC-BG=6-3=3，
∵S△GCE==×4×3=6，GF=BG=3，GE=GF+EF=3+2=5，
∴，即，
∴S△GFC=，
故答案为：45°；．
三、解答题（本大题共8小题，共62分．解答应写出文字说明、证明过程或演算步骤）
18．（1）计算：；
（2）解不等式组：，并写出它的所有整数解．
【解析】解：（1）原式＝
＝；
（2）
解不等式①得：，
解不等式②得：，
∴不等式组的解集为，
∴不等式组的整数解为1，2．
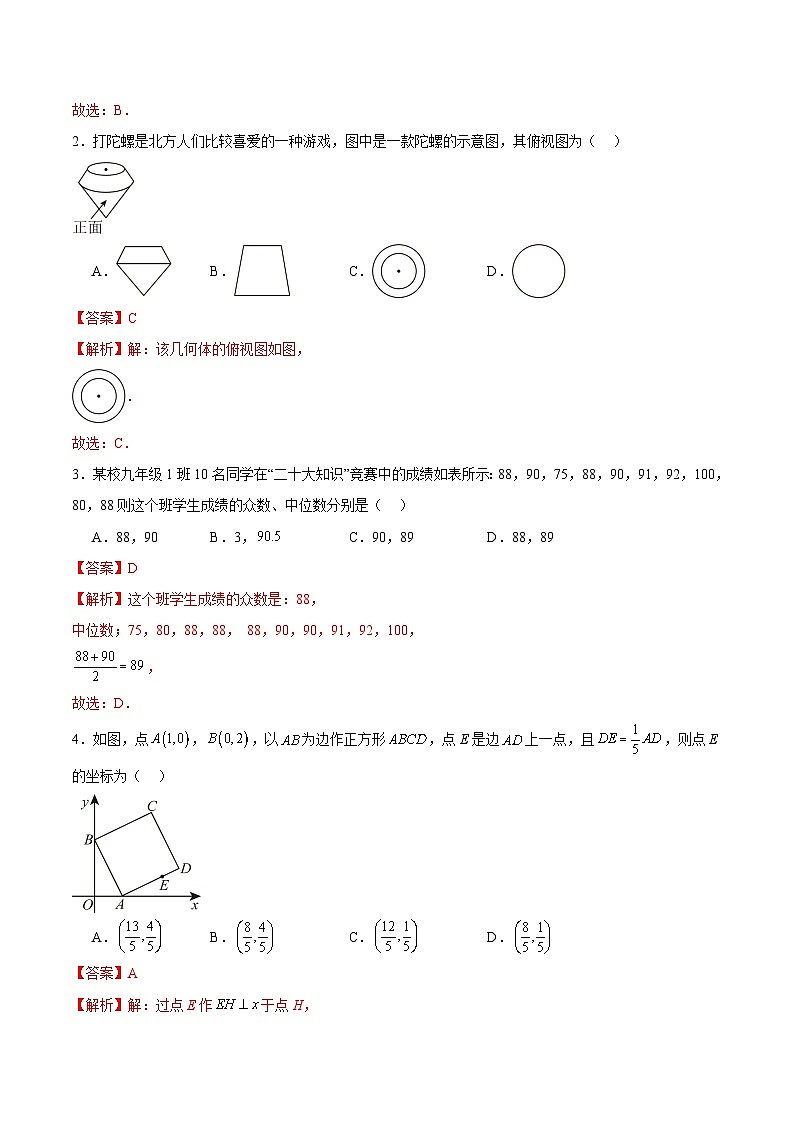
19．如图，三个顶点的坐标分别为，，．
(1)请画出关于原点的中心对称图形；
(2)在轴上找一点，使的值最小，请直接写出点的坐标 ．
【解析】（1）解：如图，即为所求；
（2）解：如图，点即为所求，由图可得，点的坐标为．
理由：∵点与点关于轴对称，
∴，
∴，
根据两点之间，线段最短，可得此时的值最小．
故答案为：．
20．已知关于x的一元二次方程．
(1)若方程有实数根，求实数m的取值范围；
(2)若方程的两个根，满足，求m的值．
【解析】（1）解：∵关于x的一元二次方程有实数根，
∴，
解得：；
（2）解：∵，是一元二次方程的两个实数根，
∴，，
∵，
∴，
即，
解得：，．
又∵在（1）中求出，
∴，
故答案为．
21．某中学为营造书香校园，计划购进甲乙两种规格的书柜放置新购置的图书，调查发现，若购买甲种书柜5个，乙种书柜2个，共需要资金1380元；若购买甲种书柜4个，乙种书柜3个，共需资金1440元．
（1）甲乙两种书柜每个的价格分别是多少元？
（2）若该校计划购进这两种规格的书柜共24个，其中乙种书柜的数量不少于甲种书柜的数量，问：学校应如何购买花费资金最少，最少资金是多少？
【解析】解：（1）设甲种书柜单价为元，乙种书柜的单价为元，由题意得：
解得
答：甲种书柜单价为180元，乙种书柜的单价为240元．
（2）设购买甲种书柜个，则购买乙种书柜个，设所需资金为元．
由题意得：．
解得
∵，随增大而减小
∴当时，（元）．
答：当购买12个甲种书柜，12个乙种书柜时，所需资金最少，最少资金为5040元．
22．如图，在中，O为的中点，过点O作交于点，交于点F．
(1)求证：四边形是菱形；
(2)若，求的长．
【解析】（1）∵四边形为平行四边形，
∴，
∴，
∵O为的中点，
∴
在与中，
，
∴，
∴
又，
∴四边形为平行四边形
又，
∴四边形为菱形．
（2）过点B作交的延长线于点G．
∵，
∴，
又∵，
∴，
设，则，
∵四边形为菱形，
∴
在中，，
∴
∴，即的长为2.8．
23．【问题提出】小慧同学遇到这样一道问题，如图①，在中，点D为边的中点，以点D为圆心，为直径作圆，的平分线交此圆于点P，点P在内部，连接．
求证，的面积等于面积的一半．
【问题解决】小慧的做法是连接并延长，交于点Q，利用形状的特殊性解决问题，请你利用小慧的做法完成【问题提出】中的证明；
【问题拓展】如图②，在四边形中平分．，若，则面积的最大值为 ．
【解析】问题解决：解：如图，连接并延长，交边于点．
∵为的直径，
∴．
∴．
∵平分，
∴．
∵，
∴．
∴．
∵．
∴点为的中点．
，
，
∴的面积等于面积的一半．
问题拓展：延长交于点，
∵平分且，
∴为等腰三角形，点为中点，
∴，
当的面积最大时，面积最大，
即满足题意，
∵，
∴面积的最大值为．
故答案为：6．
24．如图，在矩形中，点为边上一点，连接，过点作于点，交于点．
(1)如图1，当时，求证：；
(2)若，，连接，求的最小值；
(3)如图2，矩形对角线与相交于点，交于点，若平分．
①判断与的数量关系，并证明；
②连接，当的面积是矩形的时，求的值．
【解析】（1）证明：四边形是矩形，
，，
，
，
，
在和中，
，
；
（2）解：，
点在以为直径的圆上运动，
如图，取的中点，连接，当点在线段上时，取得最小值，
，
，
，
，
，即的最小值为2；
（3）解：①，
证明如下：如图，过点作交于点，
是的中点，
，
平分且，
是等腰三角形，，
，，
，
，
；
②如图2，连接，设，，
由①可知：，，
，，
在中，，
，，
，，
，
，即，
解得：，
的面积是矩形的，
，
，
，
，
．
25．下面是某数学兴趣小组探究问题的片段，请仔细阅读，并完成任务．
【问题提出】
如图1，在中，，，点D在上，请用尺规作图：在外侧，以为边作．
【问题探究】
小明：如图2，分别以B、C为圆心，以、为半径画弧，两弧交于点E，连接、则即为所求作的三角形．
小亮：如图3，过点B作于点B，过点C作于点C，、相交于点E，则即为所求作的三角形．
（1）小明得出的依据是______ ，小亮得出的依据是______ ．（横线上填序号：①；② ；③；④ ）
【问题再探】
（2）在（1）中的条件下，连接兴趣小组的同学们用几何画板测量发现和的面积相等．为了证明这个发现，A组同学会试延长线段至F点，使，连接，从而得以证明如图；B组同学过点D作于点M，过点E作于点N，从而得以证明如图，请你选取A组或B组中的一种方法完成证明过程．
【问题解决】
（3）如图6，已知，，点D在AB上，，，若在射线上存在点E，使，请求出相应的的长．
【解析】（1）解：由小明的作图可知，，，
在和中，
，
∴由小亮的作图可知，，
，
，，
，
，
，
，
在和中，
，
；
故答案为：①，③；
（2）选A组同学证明如下：延长线段至F点，使，连接，则是的中线，
，
，
，
，
，，，
即
在和中，
，
∴，
，
；
选B组同学的则证明如下：过点D作于点M，过点E作于点N，
，
≌，
，，
，
即，
在和中，
，
，
，
，，
又，
；
（3）解：过点C作交于E，于H，连接并延长交于F，
由（2）可知：，
，，
，
，
，
，
，
，
，
当时，，
，
此时，，
，
综上所述，的长为或