






所属成套资源:【赢在中考•黄金8卷】2024年中考数学全真模拟卷(多地区)
模拟卷03-【赢在中考•黄金8卷】备战2024年中考数学模拟卷(全国通用)
展开
这是一份模拟卷03-【赢在中考•黄金8卷】备战2024年中考数学模拟卷(全国通用),文件包含黄金卷03全国通用解析版docx、黄金卷03全国通用参考答案docx、黄金卷03全国通用考试版docx等3份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
1、锻炼学生的心态。能够帮助同学们树立良好的心态,增加自己的自信心。
2、锻炼学生管理时间。通过模拟考试就会让同学们学会分配时间,学会取舍。
3、熟悉题型和考场。模拟考试是很接近中考的,让同学们提前感受到考场的气氛和布局。
中考的取胜除了平时必要的学习外,还要有一定的答题技巧和良好心态。此外,通过模拟考试还能增强学生们面对高考的信心,希望考生们能够重视模拟考试。
【赢在中考·黄金8卷】备战2024年中考数学模拟卷(全国通用)
黄金卷03
(考试时间:120分钟 试卷满分:120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答填空题时,请将每小题的答案直接填写在答题卡中对应横线上。写在本试卷上无效。
4.回答解答题时,每题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上。写在本试卷上无效。
5.考试结束后,将本试卷和答题卡一并交回。
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.的相反数是( )
A.B.2024C.D.
【答案】B
【解析】解:的相反数是,
故选:.
2.下列图形中,属于轴对称图形的是( )
A.B.C.D.
【答案】A
【解析】解:A中图形是轴对称图形,故符合要求;
B中图形不是轴对称图形,故不符合要求;
C中图形不是轴对称图形,故不符合要求;
D中图形不是轴对称图形,故不符合要求;
故选:A.
3.下列计算正确的是( )
A.B.
C.D.
【答案】C
【解析】解:A. ,该选项错误;
B. ,该选项错误;
C. ,该选项正确;
D. ,该选项错误
故选:C
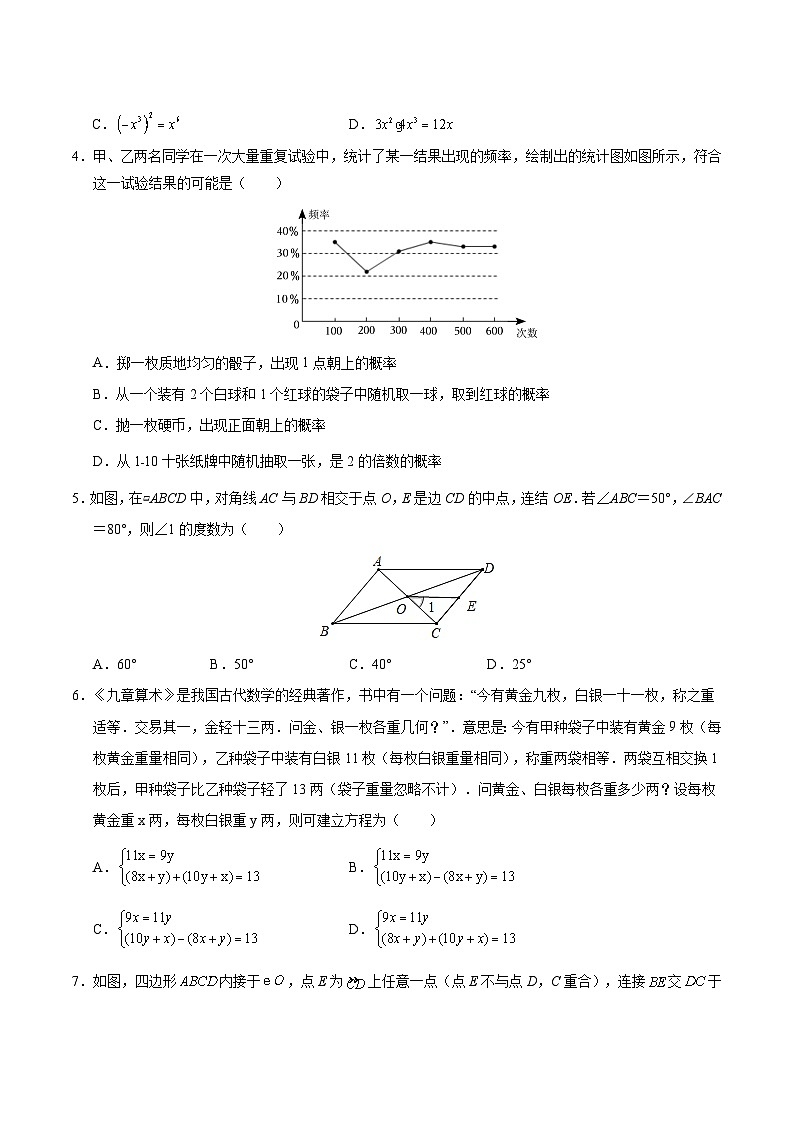
4.甲、乙两名同学在一次大量重复试验中,统计了某一结果出现的频率,绘制出的统计图如图所示,符合这一试验结果的可能是( )
A.掷一枚质地均匀的骰子,出现1点朝上的概率
B.从一个装有2个白球和1个红球的袋子中随机取一球,取到红球的概率
C.抛一枚硬币,出现正面朝上的概率
D.从1﹣10十张纸牌中随机抽取一张,是2的倍数的概率
【答案】B
【解析】解:A、掷一枚质地均匀的骰子,出现1点朝上的概率是,故此选项不符合题意;
B、从一个装有2个白球和1个红球的袋子中随机取一球,取到红球的概率是,故此选项符合题意;
C、抛一枚硬币,出现正面朝上的概率是,故此选项不符合题意;
D、从1﹣10十张纸牌中随机抽取一张,是2的倍数的概率是,故此选项不符合题意.
故选:B.
5.如图,在▱ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=50°,∠BAC=80°,则∠1的度数为( )
A.60°B.50°C.40°D.25°
【答案】B
【解析】解:∠ABC=50°,∠BAC=80°,
,
四边形是平行四边形,对角线AC与BD相交于点O,
,
E是边CD的中点,
故选B
6.《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:今有甲种袋子中装有黄金9枚(每枚黄金重量相同),乙种袋子中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲种袋子比乙种袋子轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,则可建立方程为( )
A.B.
C.D.
【答案】C
【解析】解:设每枚黄金重x两,每枚白银重y两,
依题意,得:
故选:C.
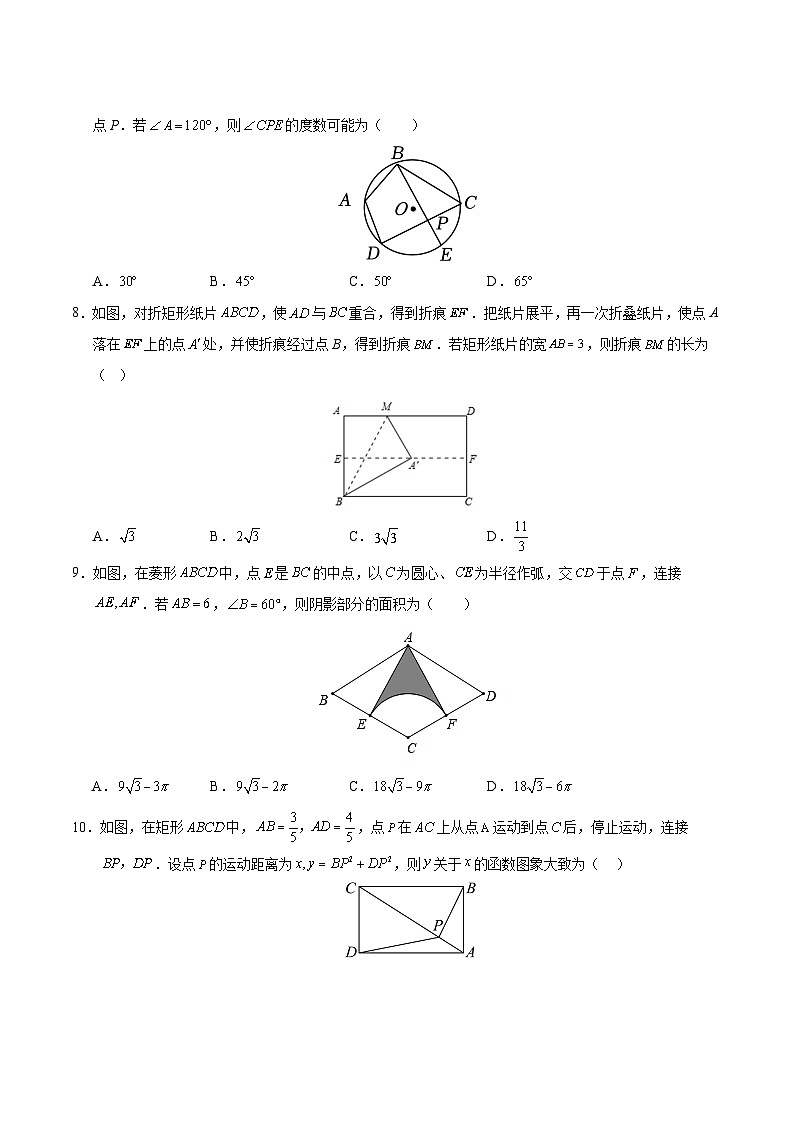
7.如图,四边形内接于,点E为上任意一点(点E不与点D,C重合),连接交于点P.若,则的度数可能为( )
A.B.C.D.
【答案】D
【解析】解:∵四边形内接于,
∴,
∵,
∴,
∵为的外角,
∴,只有D满足题意.
故选:D.
8.如图,对折矩形纸片,使与重合,得到折痕.把纸片展平,再一次折叠纸片,使点A落在上的点处,并使折痕经过点B,得到折痕.若矩形纸片的宽,则折痕的长为( )
A.B.C.D.
【答案】B
【解析】解:∵将矩形纸片对折一次,使边与重合,得到折痕,
∴.
∵再一次折叠纸片,使点A落在的处并使折痕经过点B,得到折痕,
∴.
在中,∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴
∴.
故选:B.
9.如图,在菱形中,点是的中点,以为圆心、为半径作弧,交于点,连接.若,,则阴影部分的面积为( )
A.B.C.D.
【答案】A
【解析】连接,
∵四边形是菱形,
∴,
∵,为的中点,
∴,是等边三角形,,
∵,
∴,
由勾股定理得:,
∴,
∴阴影部分的面积,
故选A.
10.如图,在矩形中,,点在上从点运动到点后,停止运动,连接.设点的运动距离为,则关于的函数图象大致为( )
A.B.
C.D.
【答案】C
【解析】解:过点作于点,过点作于点.
由题意得:,
∴,
∵,
∴,
,
在中,,
,
同理得.
在矩形中,,
在中,,
,,
,
,
即;
,
,
故选:C
二、填空题(本大题共7小题,每小题4分,共28分)
11.要使二次根式有意义,则的取值范围是 .
【答案】/
【解析】解:要使二次根式有意义,
则有,
解得,
所以,的取值范围是.
故答案为:.
12.已知则=
【答案】2.
【解析】∵
∴
∴将代入原式,可得原式.
故答案为2.
13.已知,是方程的两个实数根,则的值为 .
【答案】0
【解析】根据题意得,,
∵,是方程的两个实数根,
∴,
∴,
∴原式.
14.某商店有A,B两种糖果,原价分别为a元/千克和b元/千克.据调查发现,将两种糖果按A种糖果m千克与B种糖果n千克的比例混合,取得了较好的销售效果.现调整糖果价格,若A种糖果单价上涨,B种糖果单价下调,仍按原比例混合后,糖果单价恰好不变.则为 .
【答案】
【解析】解:根据题意得:,
即,
∴,
∴.
故答案为:.
15.如图,和是的两条弦,,分别连接.已知,则的半径长为 .
【答案】
【解析】解:连接并延长交于点连接,.
由
可得
.
在中,,
由勾股定理得
的半径长为.
故答案为:.
16.如图,矩形ABCD的顶点A、B分别在反比例函数与的图象上,点C、D在x轴上,AB、BD分别交y轴于点E、F,则阴影部分的面积为 .
【答案】5
【解析】解:设,,则
由题意知,
∴
∴
∴
解得
∴
∴
故答案为:5.
17.某数学探究小组探究一个动点问题,如图,在中,P为边上一个动点,点D在边上,已知,,,
请完成下列探究:
(1)当时,的值为 ;
(2)连接,若,则周长的最小值为 .
【答案】;
【解析】解:(1)过点D作于点M,如图:
则,
∵,
∴,
∵,
∴,
∴,
∴,
当时,,
∴,
∴;
故答案为:;
(2)若,由(1)得,
∴,
∴,
作点D关于直线的对称点,则上任意一点到点D、的距离都相等,即总有,
∴当点P在与的交点处时,的值最小,从而的值最小,最小值为的长,
∵为定长10,
∴此时,的值最小,即的周长最小,最小值是,
此时,连接,过点作于点H,如图,
∵点D与点关于直线对称,
∴垂直平分,
∴,,
∴,
∴,
∴是等边三角形,
∴,,
∴,
在中,由勾股定理,得
在中,由勾股定理,得
∴周长的最小值为,
故答案为:.
三、解答题(本大题共8小题,共62分.解答应写出文字说明、证明过程或演算步骤)
18.计算:.
【解析】解:
.
19.先化简,再求值:,其中m满足.
【解析】解:
∵m满足,
∴,
∴原式.
20.如图,C是一处钻井平台,位于某港口A的北偏东30°方向上,与港口A相距海里,一艘摩托艇从A出发,自西向东航行至点B时,改变航向以每小时50海里的速度沿BC方向航行,此时C位于B的北偏西40°方向上,则从B到达C大约需要多少小时?(结果精确到0.1小时,参考数据:,,,)
【解析】过点C作交AB于点D,如图,
∴
∴∠
在中,∠海里
∵
∴
∴(海里)
在中,∠海里,
∵,
∴ (海里)
∴从B到C用时大约为:(小时)
答:从B到达C大约需要2.3小时
21.如图,直线与反比例函数在第一象限交于点A,在第三象限交于点,与轴、轴分别交于点,已知.
(1)求一次函数和反比例函数的表达式;
(2)利用图象直接写出时的取值范围.
【解析】(1)解:由题可知点的坐标为,
,
点A的坐标为,
又点A在直线上,
,
解得(负值舍去),
一次函数的表达式为,反比例函数的表达式为.
(2)解:由题意得:,
解得:,,
,
由图可知的取值范围是或.
22.某校组织初二年级380名学生到广东南路革命化州纪念馆研学活动,已知用3辆小客车和1辆大客车每次可运送学生130人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金200元,大客车每辆租金300元.请选出最省钱的租车方案、并求出最少租金.
【解析】(1)解:设每辆小客车能坐x名学生,每辆大客车能坐y名学生,
依题意得:,
解得:.
答:每辆小客车能坐30名学生,每辆大客车能坐40名学生.
(2)解:①依题意得:,
∴,
又∵m,n均为整数,
∴或或,
∴共有3种租车方案,
方案1:租小客车2辆,大客车8辆;
方案2:租小客车6辆,大客车5辆;
方案3:租小客车10辆,大客车2辆.
②方案1所需租金为(元);
方案2所需租金为(元);
方案3所需租金为(元).
∵,
∴最省钱的租车方案是方案3租小客车10辆,大客车2辆,最少租金为2600元.
23.如图,中两条弦,互相垂直,垂足为,为的中点,连接并延长交于点.
(1)求证:;
(2)连接,求的值.
【解析】(1)解:,为的中点,
,
,
,,
,
.
(2)解:过点作于点,连接,,,,.
,,
.
同理得.
,
.
,
.
又,,
,
,即.
24.如图,在平面直角坐标系中,二次函数的图象经过点,点.
(1)求此二次函数的解析式;
(2)当时,求二次函数的最大值和最小值;
(3)点P为此函数图象上任意一点,其横坐标为m,过点P作轴,点Q的横坐标为.已知点P与点Q不重合,且线段的长度随m的增大而增大.
①求m的取值范围;
②当时,直接写出线段与二次函数的图象交点个数及对应的m的取值范围.
【解析】(1)解:将,点代入 得:
,
解得:,
∴二次函数的解析式为:;
(2),
∴抛物线开口向下,对称轴为直线 ,
∴当时,;
∵,
∴当时,;
(3)①,
当时,的长度随m的增大而减小,
当时,,的长度随m增大而增大.
∴满足题意,
解得:;
②∵,
∴,
解得:,
∵抛物线的对称轴为直线,
如图,当时,
∴,
此时抛物线与线段有1个交点,
∵抛物线上横坐标为的点关于直线的对称点的横坐标为,
当时,
∴,
如图,
此时抛物线与线段有两个交点,
当时,
∴,
如图,
此时抛物线与线段有1个交点,
综上所述, 或时,与图象交点个数为1, 时,与图象有2个交点.
25.如图1,平面上,四边形中,,,,,,点M在边上,且.点P沿折线以1个单位速度向终点C运动,点是点A关于直线的对称点,连接,设点P在该折线上运动的时间为.
(1)直接写出线段的长;
(2)如图2,连接.
①求的度数,并直接写出当、M、A共线时t的值;
②若点P到的距离为1,求的值;
(3)当时,请直接写出点到直线的距离(用含t的式子表示).
【解析】(1)解:当时,;
当时,;
(2)①,
,
又 ,
,
,
;
如图所示,当当、M、A共线时,设交与点,
∵平分,
,
∴,
,
,
,
,
,
,
,,
,
,即 ,
∴
;
②如图所示,当点在上时, ,
,
,
,
,
如图所示,当在上时,则,过点作交的延长线于点,延长交的延长线于点,
,
,
,
即
,
,
,
,
,
即,
解得:,
,
综上所述, 的值为 或 ;
(3)∵当时,在上,
如图所示,过点作于点,过点作于点,则四边形是矩形,
由 ,
,
,
设 ,
即 ,
,
,
整理得 ,
即点到直线的距离为
相关试卷
这是一份模拟卷03-【赢在中考·黄金8卷】备战2024年中考数学模拟卷(浙江专用),文件包含黄金卷03解析版docx、黄金卷03参考答案docx、黄金卷03考试版docx等3份试卷配套教学资源,其中试卷共47页, 欢迎下载使用。
这是一份模拟卷03-【赢在中考·黄金8卷】备战2024年中考数学模拟卷(深圳专用),文件包含黄金卷03解析版docx、黄金卷03参考答案docx、黄金卷03考试版docx等3份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。
这是一份模拟卷02-【赢在中考•黄金8卷】备战2024年中考数学模拟卷(全国通用),文件包含黄金卷02全国通用解析版docx、黄金卷02全国通用参考答案docx、黄金卷02全国通用考试版docx等3份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。








