




山西省朔州市2023-2024学年八年级下学期期中数学试题(原卷版+解析版)
展开一、选择题(本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求,请将正确答案的字母标号填入下表相应的空格内.)
1. 下列式子中,是二次根式的是( )
A. B. C. D.
2. 在四边形中,.如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( )
A. B. C. D.
3. 下列各式计算正确的是( )
A. B.
C D.
4. 下列命题不正确的是( )
A. 两组对边分别相等的四边形是平行四边形
B. 对角线相等平行四边形是矩形
C. 对角线互相垂直的四边形是菱形
D. 一组邻边相等的矩形是正方形
5. 如图,菱形的周长为,对角线长为,则它的面积为( )
A. B. C. D.
6. 我国秦汉时期,数学成就十分显著.当时流传这样一个数学题:今有竹高十二尺,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原本高12尺,从某处折断,竹梢触地处离竹根3尺,试问折断处距离地面多少尺?( )
A. 4.5B. 5.625C. 4D. 6.375
7. 如图在一个高为3米,长为5米的楼梯表面铺地毯,则地毯至少需要( ).
A. 3米B. 4米C. 5米D. 7米
8. 如图,已知数轴上A,B两点表示的数分别是a, b,化简的结果是( )
A. B. C. D.
9. 公元3世纪,我国数学家赵爽在《周髀算经》中巧妙地运用如图所示的“弦图”来证明勾股定理,该图是由四个全等的直角三角形和一个小正方形拼成一个大正方形,若直角三角形的较长直角边长为a,短直角边长为b,大正方形面积为20,且(a+b)=32.则小正方形的面积为( )
A. 6B. 8C. 10D. 12
10. 如图,面积为5的正方形的顶点在数轴上,且表示的数为1,若点在数轴上,(点在点的右侧)且,则点所表示的数为( )
A. B. C. D.
二、填空题(每小题3分,共15分)
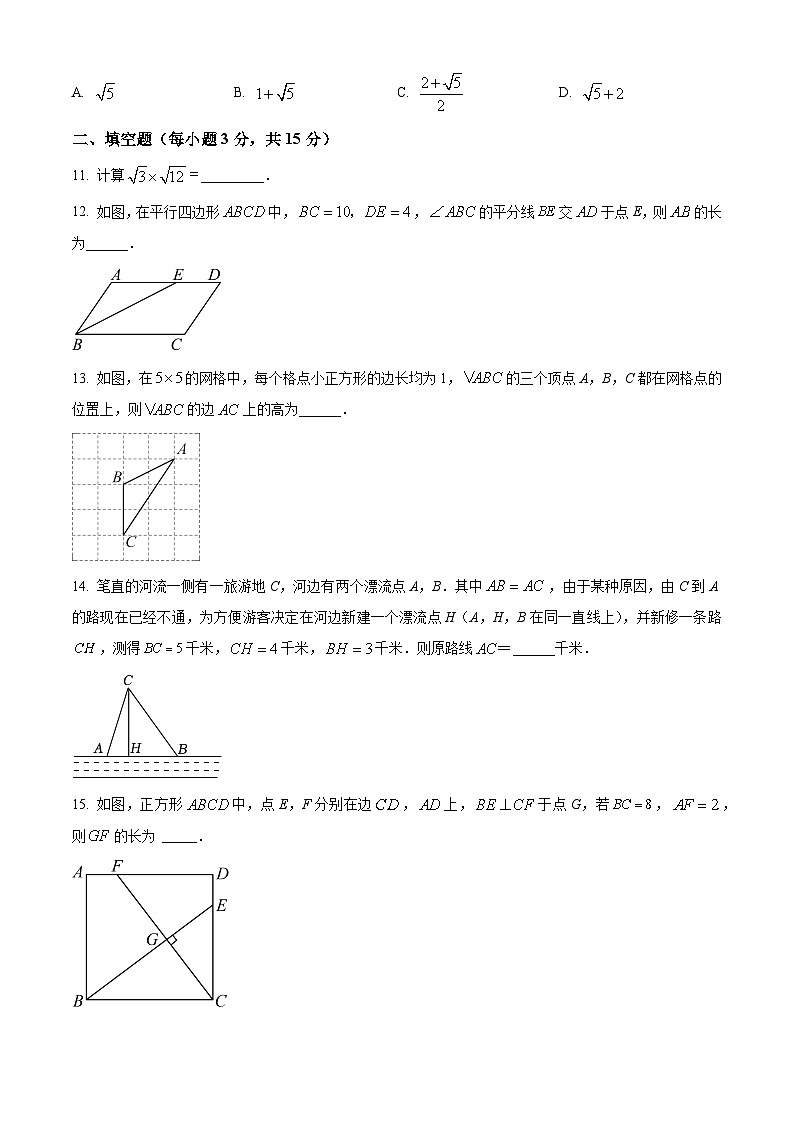
11. 计算_________.
12. 如图,在平行四边形中,,的平分线交于点E,则的长为______.
13. 如图,在的网格中,每个格点小正方形的边长均为1,的三个顶点A,B,C都在网格点的位置上,则的边上的高为______.
14. 笔直的河流一侧有一旅游地C,河边有两个漂流点A,B.其中,由于某种原因,由C到A的路现在已经不通,为方便游客决定在河边新建一个漂流点H(A,H,B在同一直线上),并新修一条路,测得千米,千米,千米.则原路线______千米.
15. 如图,正方形中,点E,F分别在边,上,于点G,若,,则的长为 _____.
三、解答题(本大题共8个小题,共75分,解答应写出文字说明,证明过程或演算步骤)
16. 计算:
(1)
(2)
(3)
17. 下面是小文同学进行二次根式混合运算的过程,请认真阅读,完成相应的任务:
任务:
(1)上述解答过程中,第1步依据的乘法公式为 (用字母表示);
(2)上述解答过程,从第 步开始出错,具体的错误是 ;
(3)计算正确结果为 .
18. 如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,其中点A.B.C.D均在小正方形的顶点上.
(1)在方格纸中画出锐角等腰△ABE,点E在小正方形的顶点上,且的面积为10;
(2)在方格纸中画出等腰直角△CDF,点F在小正方形的顶点上,且的面积为10;
(3)在(1)(2)条件下,连接EF,请直接写出线段EF长.
19. 一物体从高处自由落下,落到地面所用的时间(单位:秒)与开始落下时的高度h(单位:米)有下面的关系式:.
(1)已知米,求落下所用时间;
(2)一人手持一物体从五楼让它自由落到地面,约需多少时间?(无地下室,每层楼高约3.5米,手拿物体高为1米)
(3)如果一物体落地的时间为3.6秒,求物体开始下落时的高度.
20. 小明和小亮学习了“勾股定理”之后,为了测量风筝的垂直高度,他们进行了如下操作:
①测得水平距离长为15米:
②根据手中剩余线的长度计算出风筝线的长为25米;
③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度;
(2)如果小明想风筝沿方向下降12米,则他应该往回收线多少米?
21. 如图,在平行四边形ABCD中,BE平分∠ABC,延长BE交AD的延长线于点F,延长ED至点G,使,分别连接AE,AG,FG.
(1)求证:;
(2)当E为CD边的中点时,判断四边形AEFG的形状,并说明理由.
22. 阅读与思考,阅读下列材料,完成相应的任务.
欧几里德数
一般地,给定单位长度1,一个数如果可以借助图形构造出来,我们就称这个数为欧几里德数.例如,如图1所示的方格图中,设每个小正方形的边长为单位1.借助方格图,可以构造出线段AB,CD,EF分别表示正整数2,3,4,也可以构造出线段MN表示正分数.事实上,所有的正有理数都是欧几里德数.
任务:如图2,图3,图4所示的方格图中,每个小正方形的边长均为单位长度1.
(1)请在图2中用两种方法构造线段表示正整数5(该线段的端点均为格点);
(2)小彬由材料中的结论出发展开联想,经过探究,发现正无理数,也是欧几里德数,可分别用图3中两个三角形的边XY,PQ表示,其思考与作图方法如下:
,取网格中,且,连接XY,则.
,取网格中线段,,以点O为圆心,ON长为半径作弧交网格线于点P,连接OP,且,则.
在图4中借助网格和尺规,用两种方法构造三角形,使三角形的一边表示欧几里德数(保留作图痕迹,不写作法).
23. 学习正方形时,王老师带领同学们探索了课本上的一道几何题.
【课本原型】(1)人教版八年级下册数学课本拓广探索》第15题.请你写出证明过程.
【问题解决】(2)如图(1),正方形中,点G为延长线上的任意一点,交延长线于点E,交于点F.试探索、、之间的数量关系,并给出证明
【问题研究】(3)如图(2),四边形是正方形,点G为上的一点,于点E,连接,若,请直接写出的面积.
解:
…第1步
…第2步
…第3步
…第4步
如图,四边形是正方形,点G为上的任意一点,于点E、,交于F.求证:.
山西省太原市杏花岭区山西省实验中学2023-2024学年八年级下学期期中数学试题(原卷版+解析版): 这是一份山西省太原市杏花岭区山西省实验中学2023-2024学年八年级下学期期中数学试题(原卷版+解析版),文件包含山西省太原市杏花岭区山西省实验中学2023-2024学年八年级下学期期中数学试题原卷版docx、山西省太原市杏花岭区山西省实验中学2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
山西省实验中学2023-2024学年七年级下学期期中数学试题(原卷版+解析版): 这是一份山西省实验中学2023-2024学年七年级下学期期中数学试题(原卷版+解析版),文件包含山西省实验中学2023-2024学年七年级下学期期中数学试题原卷版docx、山西省实验中学2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
山西省介休市2023-2024学年七年级下学期期中数学试题(原卷版+解析版): 这是一份山西省介休市2023-2024学年七年级下学期期中数学试题(原卷版+解析版),文件包含山西省介休市2023-2024学年七年级下学期期中数学试题原卷版docx、山西省介休市2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。












