广东省茂名市信宜市2023-2024学年八年级下学期期中数学试卷(含答案)

这是一份广东省茂名市信宜市2023-2024学年八年级下学期期中数学试卷(含答案)，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．下列是一元一次不等式的是( )
A.B.C.D.
2．在直角坐标系中，点P（﹣2，3）向右平移3个单位长度后的坐标为( )
A.（﹣2，6）B.（1，3）C.（1，6）D.（﹣5，3）
3．以下列数据为长度的线段中，可以构成直角三角形的是( )
A.1，，B.，3，5C.1，2，3D.2，3，4
4．如图，哪一个选项的右边图形可由左边图形平移得到( )
A.B.C.D.
5．若等腰三角形的两边长分别为2和5，则它的周长为( )
A.9B.7C.12D.9或12
6．如图，直线a、b分别经过等边三角形ABC的顶点A、C，且a∥b，∠1＝42°，则∠2的度数为( )
A.18°B.42°C.60°D.102°
7．已知，下列不等式一定成立的是( )
A.B.C.D.
8．如图，以每秒的速度沿着射线向右平移，平移秒后所得图形是，那么的长是( )
A.4B.6C.8D.9
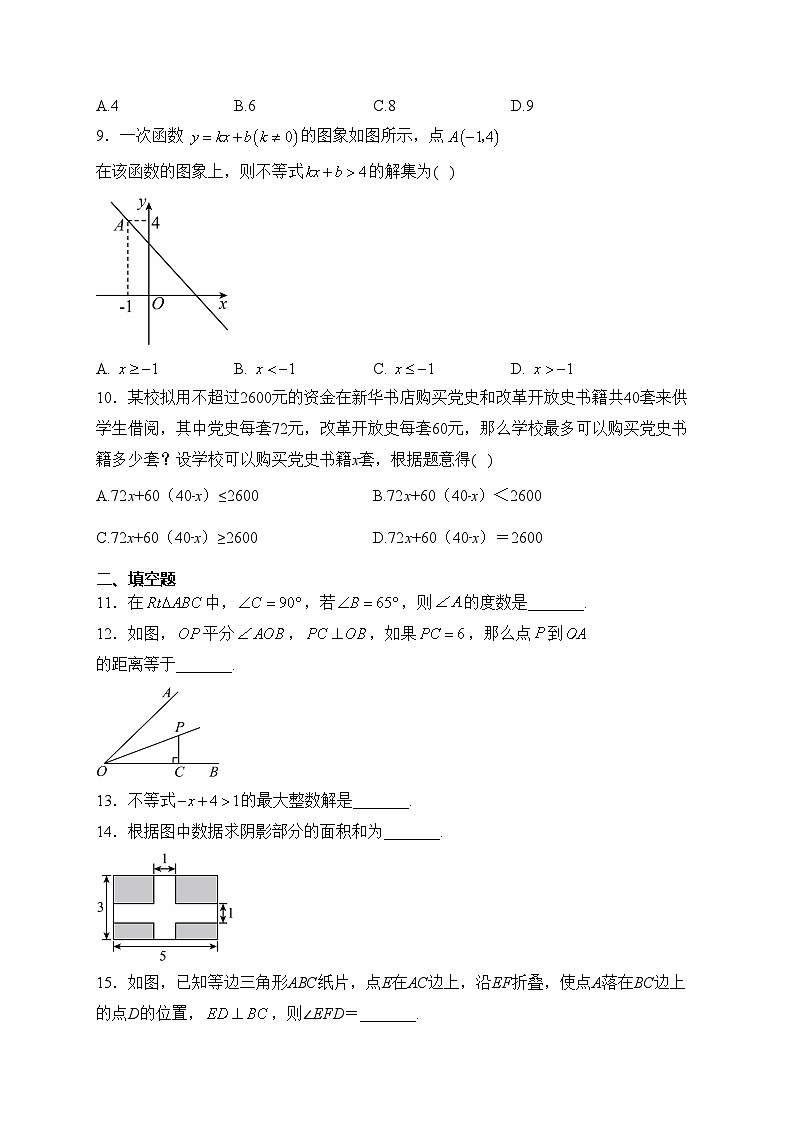
9．一次函数 的图象如图所示，点在该函数的图象上，则不等式的解集为( )

A. B. C. D.
10．某校拟用不超过2600元的资金在新华书店购买党史和改革开放史书籍共40套来供学生借阅，其中党史每套72元，改革开放史每套60元，那么学校最多可以购买党史书籍多少套？设学校可以购买党史书籍x套，根据题意得( )
A.72x+60（40﹣x）≤2600B.72x+60（40﹣x）＜2600
C.72x+60（40﹣x）≥2600D.72x+60（40﹣x）＝2600
二、填空题
11．在中，，若，则的度数是_______.
12．如图，平分，，如果，那么点到的距离等于_______.
13．不等式的最大整数解是_______.
14．根据图中数据求阴影部分的面积和为_______.
15．如图，已知等边三角形ABC纸片，点E在AC边上，沿EF折叠，使点A落在BC边上的点D的位置，，则∠EFD＝_______.
三、解答题
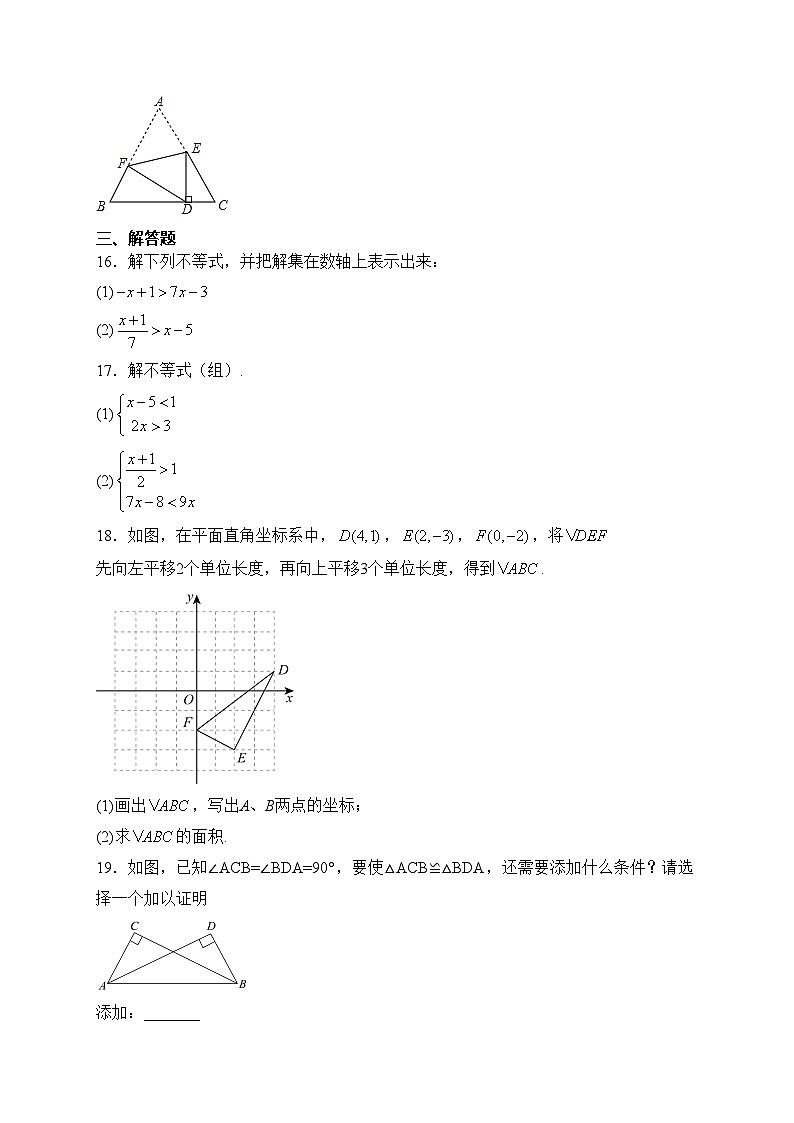
16．解下列不等式，并把解集在数轴上表示出来：
(1)
(2)
17．解不等式（组）.
(1)
(2)
18．如图，在平面直角坐标系中，，，，将先向左平移2个单位长度，再向上平移3个单位长度，得到.
(1)画出，写出A、B两点的坐标；
(2)求的面积.
19．如图，已知∠ACB=∠BDA=90°，要使△ACB≌△BDA，还需要添加什么条件？请选择一个加以证明
添加：_______
选择：_______
证明：
20．如图，函数和的图象相交于点.
(1)求m，a的值；
(2)根据图象，直接写出不等式的解集.
21．我市在创建全国文明城市过程中，决定购买A，B两种树苗对某路段道路进行绿化改造，已知购买A种树苗8棵，B种树苗2棵，需要900元；购买A种树苗5棵，B种树苗4棵，需要700元.
(1)求购买A，B两种树苗每棵各需多少元？
(2)考虑到绿化效果和资金周转，购进A种树苗不能少于32棵，且用于购买这两种树苗的资金不能超过5750元，若购进这两种树苗共80棵，则有哪几种购买方案？
22．如图，在ABC中，D是边BC的中点，E是边AC的中点，连接AD，BE.
(1)若CD＝8，CE＝6，AB＝20，求证：∠C＝90°；
(2)若∠C＝90°，AD＝13，AE＝6，求ABC的面积.
23．（1）用“<”“>”或“=”填空：
_______；
______；
______；
______.
（2）观察以上各式，你发现它们有什么规律吗？你能用一个含有字母a，b的式子表示上述规律吗？
（3）运用你所学的知识说明你发现的规律的正确性.
24．（综合与实践）已知，在等边三角形中，点E在上，点D在的延长线上，且.
(1)【特殊情况，探索结论】如图1，当点E为的中点时，确定线段与的大小关系，请你直接写出结论：______（填“”、“”或“”）；
(2)【特例启发，解答题目】如图2，当点E为边上任意一点时，确定线段与DB的大小关系，请你直接写出结论，______（填“”、“”或“”）；理由如下，过点E作，交于点F.（请你完成以下解答过程）：
(3)【拓展结论，设计新题】如图3，在等边三角形中，点E在直线上，点D在线段的延长线上，且，若的边长为1，，求的长（直接写出结果）.
参考答案
1．答案：C
解析：A、中不是整式，不是一元一次不等式，故本选项错误；
B、中不含有不等符号，不是一元一次不等式，故本选项错误；
C、含有一个未知数，未知数的最高次数是1，是一元一次不等式，故本选项正确；
D、中含有一个未知数，但未知数的最高次数等于2，不是一元一次不等式，故本选项错误.
故选：C.
2．答案：B
解析：平移后点P的横坐标为﹣2+3＝1，纵坐标不变为3
所以点P（－2，3）向右平移3个单位长度后的坐标为（1，3）
故选B.
3．答案：A
解析：A、∵，
∴三边长为1，，，可以组成直角三角形，故此选项符合题意；
B、∵，
∴三边长为，3，5，不可以组成直角三角形，故此选项不符合题意；
C、∵，
∴三边长为1，2，3，不可以组成直角三角形，故此选项不符合题意；
D、∵，
∴三边长为2，3，4，不可以组成直角三角形，故此选项不符合题意；
故选：A.
4．答案：C
解析：由平移的概念得选项C是正确的.
故选：C.
5．答案：C
解析：（1）若2为腰长，5为底边长，
由于，则三角形不存在；
（2）若5为腰长，则，符合三角形的两边之和大于第三边.
所以这个三角形的周长为.
故选：C.
6．答案：D
解析：在等边三角形ABC中
又∵
∴
故选D
7．答案：D
解析：A、由，可知，该选项错误，不符合题意；
B、由，可知，该选项错误，不符合题意；
C、由，可知，该选项错误，不符合题意；
D、由，可知，该选项正确，符合题意；
故选：D.
8．答案：A
解析：∵以每秒的速度沿着射线向右平移，平移秒后所得图形是，
∴，
故选：A.
9．答案：B
解析：由图象可得：当时，，
所以不等式的解集为，
故选：B.
10．答案：A
解析：设学校可以购买党史书籍x套，则购买改革开放史书籍（40﹣x）套，
则根据题意得：72x+60（40﹣x）≤2600.
故选A
11．答案：25°
解析：∵在中，， ，
∴∠A=180°-∠C-∠B=25°
故答案为：25°.
12．答案：6
解析：过作于，
平分，，
，
点到的距离等于6.
故答案为：6.
13．答案：2
解析：，
，
，
∴最大整数解是2，
故答案为：2.
14．答案：8
解析：由图可知，阴影部分的面积＝.
故答案为：8.
15．答案：45°
解析：∵是等边三角形
沿EF折叠，使点A落在BC边上的点D的位置，
∴
故答案为：45°
16．答案：(1)，数轴表示见详解
(2)，数轴表示见详解
解析：（1）
，
解得：，
∴原不等式的解集为：；
数轴表示为：
（2）
解得：
∴原不等式的解集为：.
数轴表示为：
17．答案：(1)
(2)
解析：（1），
解不等式①，得，
解不等式②，得，
所以不等式组的解集是；
（2），
解不等式①，得，
解不等式②，得，
所以不等式组的解集是.
18．答案：(1)图见详解；点A坐标为，点B坐标为；
(2)5
解析：（1）如图所示，即为所作，
点A坐标为，点B坐标为；
（2）.
19．答案：∠CAB=∠DBA或∠CBA=∠DAB或CA=DB或BC=AD；∠CAB=∠DBA（答案不唯一），证明见解析
解析：∵∠ACB=∠BDA=90°，AB=BA
∴若添加∠CAB=∠DBA，利用AAS即可证出△ACB≌△BDA；
若添加∠CBA=∠DAB，利用AAS即可证出△ACB≌△BDA；
若添加CA=DB，利用HL即可证出△ACB≌△BDA；
若添加BC=AD，利用HL即可证出△ACB≌△BDA；
如选择∠CAB=∠DBA
证明：在△ACB和△BDA中
∴△ACB≌△BDA
故答案为：∠CAB=∠DBA或∠CBA=∠DAB或CA=DB或BC=AD；∠CAB=∠DBA（答案不唯一）
20．答案：(1)，
(2)＞
解析：（1）把代入得，，
解得：，
∴点A的坐标为，
∵函数的图象经过点A，
∴，
解得：；
（2）由图象得，不等式的解集为：.
21．答案：(1)A种树苗每棵100元，B种树苗每棵50元
(2)4种，见解析
解析：（1）设A种树苗每棵x元，B种树苗每棵y元，
根据题意，得，
解得，
答：A种树苗每棵100元，B种树苗每棵50元.
（2）设购进A种树苗m棵，则购进B种树苗棵，
根据题意，得：，
解得：，
∵m为正整数，
∴或33或34或35，
所以购买的方案有：
①购进A种树苗32棵，B种树苗48棵；
②购进A种树苗33棵，B种树苗47棵；
③购进A种树苗34棵，B种树苗46棵；
④购进A种树苗35棵，B种树苗45棵.
22．答案：(1)见解析
(2)60
解析：（1）证明：是边的中点，是边的中点，，，
，，
，
，
是直角三角形，
；
（2）是边的中点，，
.
在中，，，，
，
，
的面积.
23．答案：（1）>，=，>，=
（2）任意两个数的平方和大于或等于这两个数乘积的2倍，即a2+b2≥2ab
（3）见解析
解析：（1）52+32＞2×5×3；
32+32=2×3×3.
（-3）2+22＞2×（-3）×2；
（-4）2+（-4）2=2×（-4）×（-4）；
故答案为：>，=，>，=；
（2）一般结论是：任意两个数的平方和大于或等于这两个数乘积的2倍，即有a2+b2≥2ab；
（3）∵（a-b）2≥0，
∴a2-2ab+b2≥0，
∴a2+b2≥2ab.
24．答案：(1)
(2)
(3)3
解析：（1）∵等边三角形，
∴，，
∵点E为的中点
∴，，
∵，
∴，
∵，
∴，
∴；
故答案为：；
（2），理由如下：
过点E作，交于点F，
∵为等边三角形，
∴，，
∵，
∴，
∴为等边三角形，
∴，
∴，
∵，
∴，
∵，
∴，
在△DBE和△EFC中，
，
∴，
∴，
∴；
故答案为：；
（3）由题意，点在线段的延长线上，作，则，
∵，
∴为等边三角形，
∴，
同（2）可得，
∴，
∵，
∴，
∴，
∵，
∴.