北师大版七年级下册6 完全平方公式图文ppt课件

这是一份北师大版七年级下册6 完全平方公式图文ppt课件，共22页。PPT课件主要包含了学习目标，导入新课，a2+2ab+b2，a2-2ab+b2，乘积的2倍，新知探究，典例精析，当堂练习，x2+8，课堂小结等内容，欢迎下载使用。

1.进一步掌握完全平方公式；2.灵活运用完全平方公式进行计算．(重点，难点)
1.完全平方公式:(a+b)2=　 　　　　; (a-b)2=　 　　　　. 即两数和(或差)的平方，等于它们的平方和，加上(或减去)它们的　　　　　　. 
2.简记为：首平方，尾平方，积的两倍放中央，和是加差是减．
有一个王国的公主被妖怪抓到了森林里,两个农夫一起去森林打猎时打死了妖怪救出了公主,国王要赏赐他们.这两个农夫原来各有一块边长为a米的正方形土地,第一个农夫就对国王说:“您可不可以再给我一块边长为b米的正方形土地呢?”国王答应了他,国王问第二个农夫:“你是不是要跟他一样啊?”第二个农夫说:“不,我只要您把我原来的那块地的边长增加b米就好了”.国王想不通了,他说:“你们的要求不是一样的吗?”
第一个农民的土地扩大后面积为(a2+b2)米2,第二个农民的土地扩大后面积为(a+b)²米2.【思考】　a²+b²与(a+b) ²有什么关系?
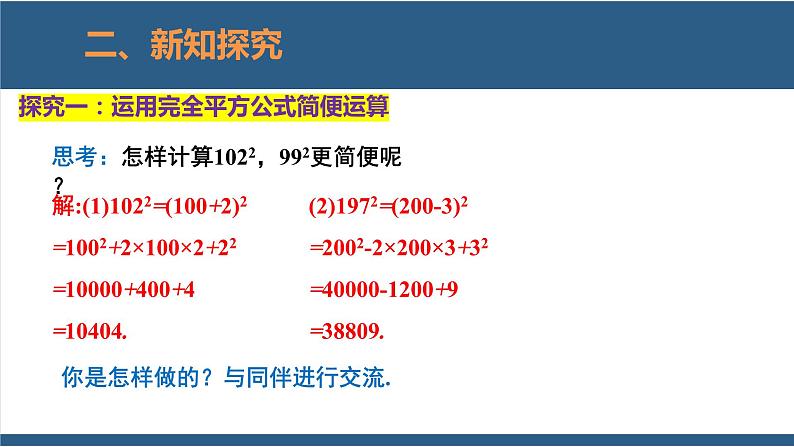
探究一：运用完全平方公式简便运算
思考：怎样计算1022，992更简便呢？
解:(1)1022=(100+2)2=1002+2×100×2+22=10000+400+4=10404.
(2)1972=(200-3)2=2002-2×200×3+32=40000-1200+9=38809.
你是怎样做的？与同伴进行交流.
解:(1)原式=(100-0.2)2=1002-2×100×0.2+0.04=10000-40+0.04=9960.04.
计算:(1)(x+3)2-x2;　 (2)(a+b+3)(a+b-3); (3)(x+5)2-(x-2)(x-3).
解:(1)方法一:(x+3)2-x2 =x2+6x+9-x2 =6x+9.
(2)(a+b+3)(a+b-3)=[(a+b)+3][(a+b)-3]=(a+b)2-32=a2+2ab+b2-9.
(3)(x+5)2-(x-2)(x-3)=x2+10x+25-(x2-5x+6)=x2+10x+25-x2+5x-6=15x+19.
探究二：综合利用乘法公式进行计算
方法二:逆用平方差公式(x+3)2- x2=(x+3+x)(x+3- x)=(2x+3)·3=6x+9.
想一想：有几种计算方法？
(1)在计算两数的平方差时，若底数是多项式，则可以直接利用完全平方公式展开后，再合并同类项，也可以把它看成一个整体，逆用平方差公式计算.(2)不能直接应用公式进行计算的式子,可能需要先添括号变形成符合公式的要求才行;(3)减去多项式乘多项式时，需注意添括号.
做一做：有一位老人非常喜欢孩子,每当有孩子到他家做客时,老人都要拿出糖果招待他们.如果来1个孩子,老人就给这个孩子1块糖果;如果来2个孩子,老人就给每个孩子2块糖果;如果来3个孩子,老人就给每个孩子3块糖果…… 假如第一天有a个孩子一起去看老人，第二天有b个孩子一起去看老人,第三天有(a+b)个孩子一起去看老人，那么第三天老人给出去的糖果和前两天给出去的糖果总数一样多吗？
请你用所学的公式解释自己的结论.
解:第三天得到的糖果总数多,多2ab块.因为(a+b)2-(a2+b2)=a2+2ab+b2-a2-b2=2ab.
探究三：完全平方公式的常见变形及应用
2.已知a+b=3,ab=1,求:(1)a2+b2的值; (2)(a-b)2的值.
解:(1)a2+b2=(a+b)2-2ab=32-2×1=7.
(2)(a-b)2=(a+b)2-4ab=32-4×1=5.
灵活运用(a±b)2,a2+b2,ab之间的关系变形:(1)a2+b2=(a+b)2-2ab=(a-b)2+2ab;(2)(a+b)2-(a-b)2=4ab;(3)(a+b)2+(a-b)2=2(a2+b2).
例1：借助乘法公式计算:(1)79.82; (2)1992-201×199.
解:(1)79.82=(80-0.2)2=802-2×80×0.2+0.22=6400-32+0.04=6368.04.
(2)1992-201×199=(200-1)2-(200+1)(200-1)=2002-2×200+1-(2002-1)=2002-400+1-2002+1=-400+2=-398.
例2：计算:(1)(x+2y-3)(x+2y+3); (2)(2a-b+c)(2a+b-c).
解:(1)原式=[(x+2y)-3][(x+2y)+3]=(x+2y)2-32=x2+4xy+4y2-9.
(2)原式=[2a-(b-c)][2a+(b-c)]=(2a)2-(b-c)2=4a2-b2+2bc-c2.
例3：已知a+b=10,a2+b2=4,求ab的值.
解:因为(a+b)2=a2+2ab+b2,所以102=4+2ab,所以100=4+2ab,解得ab=48.
1.将9.52变形,正确的是(　　)+0.52 (10+0.5)(10-0.5)×10×0.5+0.52 +9×0.5+0.52
2.下列计算正确的是(　　)A.(b-4c)2=b2-16c2 B.(a-2bc)2=a2+4abc+4b2c2C.(x+y)2=x2+xy+y2 D.(4m-n)2=16m2-8mn+n2
3.若(a+b)2=(a-b)2+A,则A为(　　)A.2ab B.-2abC.4ab D.-4ab
4.一个长方形的长、宽分别为a,b,周长为14,面积为10,则a2+b2等于(　　)A.27B.29C.31D.32
7.一个正方形的边长增加3 cm,它的面积就增加45 cm2,则这个正方形的边长是　　　　. 
6.化简:(x+2)2+4(1-x)=　　　　. 
8.若a+b+c=4,ab+bc+ca=4,则a2+b2+c2的值为　　　　. 
9.运用完全平方公式计算：(1) 962 ； (2) 2032 .
解：(1)原式=(100-4)2=1002+42-2×100×4=10000+16-800=9216；
(2)原式=(200+3)2=2002+32++2×200×3=40000+9+1200=41209.
10.计算:(1)(x+1)2-(x+2)(x-2); (2)(a+2b)(a-2b)+(a+2b)2-4ab; (3)(2a-b+c)(2a+b-c).
解:(1)原式=x2+2x+1-x2+4 =2x+5.
(3)原式=[2a-(b-c)][2a+(b-c)]=(2a)2-(b-c)2=4a2-b2+2bc-c2.
(2)原式=a2-4b2+a2+4ab+4b2-4ab =2a2.
11.若a+b=5,ab=－6, 求a2+b2,a2－ab+b2.
解：a2+b2 =（a+b)2－2ab =52-2×(－6) =37；
a2－ab+b2=a2+b2－ab=37－(－6)=43.
12.胜利公园有一块正方形草坪,需要修整成一块长方形草坪,在修整时一边加长了4 m,与其相邻的一边减少了4 m,这时得到的长方形草坪的面积与原来正方形草坪的边长减少了2 m后的面积相等,求原正方形草坪的面积是多少.
解:设原正方形草坪的边长为x m.根据题意,得(x+4)(x-4)=(x-2)2,x2-16=x2-4x+4,4x=20,x=5.所以原正方形草坪的面积为52=25(m2).