2022-2023学年河北省邯郸市馆陶实验中学、陶山中学八年级（下）期中数学试卷（含解析）

这是一份2022-2023学年河北省邯郸市馆陶实验中学、陶山中学八年级（下）期中数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.函数y= x−4的自变量x的取值范围是( )
A. x>4B. x≠4C. x≥4D. x≤4
2.为了解某市参加中考的26000名学生的身高情况，抽查了其中1300名学生的身高进行统计分析，下面叙述正确的是( )
A. 26000名学生是总体B. 1300名学生的身高是样本
C. 样本容量是1300名D. 这次调查是全面调查
3.某辆速度为v(km/h)的车从甲地开往相距s(km)的乙地，全程所用的时间为t(h)，在这个变化过程中，( )
A. s是变量B. t是常量C. v是常量D. s是常量
4.下列图象中，表示y是x的函数的是( )
A. B.
C. D.
5.在平面直角坐标系中，第四象限内有一点M(3,−4)，它到x轴的距离为( )
A. 3B. −3C. 4D. −4
6.我县某荔枝基地，2021年荔枝产量比2020年增长8.5%，2022年比2021年增长了9.4%.若2020年和2022年该基地荔枝产量分别为a万斤和b万斤，则a，b之间满足的关系式是( )
A. b=a(1+8.5%+9.4%)B. b=a(1+8.5%×9.4%)
C. b=a(1+8.5%)(1+9.4%)D. b=a(1+8.5%)2(1+9.4%)
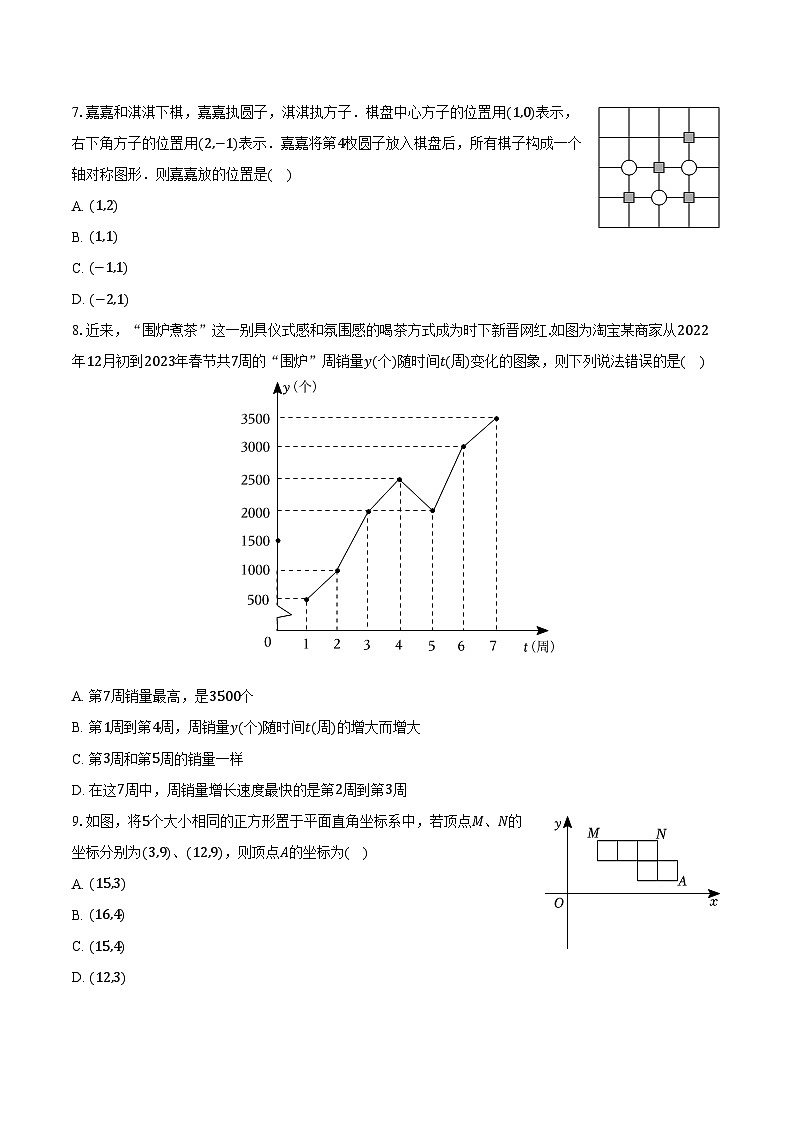
7.嘉嘉和淇淇下棋，嘉嘉执圆子，淇淇执方子．棋盘中心方子的位置用(1,0)表示，右下角方子的位置用(2,−1)表示．嘉嘉将第4枚圆子放入棋盘后，所有棋子构成一个轴对称图形．则嘉嘉放的位置是( )
A. (1,2)
B. (1,1)
C. (−1,1)
D. (−2,1)
8.近来，“围炉煮茶”这一别具仪式感和氛围感的喝茶方式成为时下新晋网红.如图为淘宝某商家从2022年12月初到2023年春节共7周的“围炉”周销量y(个)随时间t(周)变化的图象，则下列说法错误的是( )
A. 第7周销量最高，是3500个
B. 第1周到第4周，周销量y(个)随时间t(周)的增大而增大
C. 第3周和第5周的销量一样
D. 在这7周中，周销量增长速度最快的是第2周到第3周
9.如图，将5个大小相同的正方形置于平面直角坐标系中，若顶点M、N的坐标分别为(3,9)、(12,9)，则顶点A的坐标为( )
A. (15,3)
B. (16,4)
C. (15,4)
D. (12,3)
10.某城市出租车的起步价为10元(即行驶距离在3千米及以内付10元车费)，超过3千米后，1千米加2元(不足1千米按1千米计).小张在该市乘出租车从甲地到乙地，支付车费22元，则从甲地到乙地的路程最多有( )
A. 11千米B. 10千米C. 9千米D. 8千米
11.在平面直角坐标系中，A(1,0)，B(0,−3)，点B绕点A逆时针旋转90°得到点C，则点C的坐标是( )
A. (4,0)B. (4,−1)C. (3,0)D. (3,−1)
12.一次数学测试后，数学老师把本班40名学生的成绩分为5组进行统计，这5组数据的频数依次是12，10，4，8，6，若把这5组数据绘制成扇形统计图，则在扇形统计图中，频数“6”对应的圆心角等于( )
A. 36°B. 54°C. 72°D. 108°
13.在平面直角坐标系中，已知A(4,3)，A′与A关于直线x=1轴对称，则A′的坐标为( )
A. (−4,3)B. (4,−1)C. (−2,3)D. (4,−3)
14.如图是一组有规律的图案，它们是由边长相等的正三角形组合而成，第1个图案有4个角形，第2个图案有7个三角形，第3个图案有10个三角形，按此规律摆下去，若第n个图案中有y个三角形，则y与n之间的关系式是( )
A. y=2n+1B. y=2n−1C. y=3n+1D. y=3n−1
15.肥料的施用量与产量之间有一定的关系.研究表明，当每公顷钾肥和磷肥的施用量一定时，土豆的产量与氮肥的施用量有如下关系：
根据表格可知，下列说法正确的是( )
A. 氮肥施用量越大，土豆产量越高
B. 氮肥施用量是110kg时，土豆产量为32t
C. 如果不施氮肥，土豆的产量是15.18吨/公顷
D. 土豆产量为39.45t时，氮肥的施用量一定是202kg
16.根据如图所示的程序计算函数y的值，若输入的x的值为−1和5时，输出的y的值相等，则b等于( )
A. 4B. −4C. −2D. 2
二、填空题：本题共3小题，每小题3分，共9分。
17.在平面直角坐标系中，点M(−4,1)，先向右平移2个单位，再作关于y轴对称，最后得到的点的坐标为______．
18.下面是某市2017−2020年私人汽车拥有量和年增长率的统计图，该市2020年私人汽车拥有量比前一年增加了______万辆，私人汽车拥有量年增长率最大的是______年.
19.某油库有一储油量为40吨的储油罐，在开始的一段时间内只开进油管，不开出油管；在随后的一段时间内既开进油管，又开出油管直至储油罐装满油.若储油罐中的储油量(吨)与时间(分)的函数关系如图所示．
(1)每分钟的进油量为______吨，每分钟的出油量为______吨；
(2)现将装满油的储油罐只开出油管，不开进油管，则放完全部油所需的时间是______分钟．
三、解答题：本题共7小题，共69分。解答应写出文字说明，证明过程或演算步骤。
20.(本小题9分)
如图，这是某校的平面示意图(图中每个小正方形的边长为1个单位长度)，由于保管不善，现只知道初中楼的坐标是(−4,2)，实验楼的坐标是(−4,0)．
(1)为了还原原直角坐标系，则应该以______为原点，建立平面直角坐标系，请在图中画出该坐标系；
(2)写出校门、图书馆和操场的坐标．
21.(本小题9分)
已知一个长方形的长为x，宽为y，周长为40．
(1)求出y关于x的函数表达式(不用写出自变量x的取值范围)；
(2)当x=12时，求该长方形的面积．
22.(本小题9分)
在平面直角坐标系中，已知点M(m−1,2m+4)．
(1)若点M在y轴上，求m的值．
(2)若点M在二、四象限的角平分线上，求点M的坐标．
23.(本小题10分)
国际足联世界杯(FIFA Wrld Cup)，简称“世界杯”，是由全世界国家级别球队参与，象征足球界最高荣誉，并具有最高知名度和最大影响力的足球赛事.世界杯每四年举办一次，任何国际足联会员国(地区)都可以派出代表队报名参加这项赛事.第22届世界杯足球赛在卡塔尔举行，为了解同学们对卡塔尔世界杯的了解情况，某数学兴趣小组利用课余时间在全校抽取了部分学生进行问卷调查，将调查结果分为四个等级(A.不了解；B.了解较少；C.了解较多；D.十分了解)进行统计.并将统计结果绘制成如下两幅不完整的统计图：

请你根据统计图提供的信息，解答下列问题：
(1)求被调查的学生总人数．
(2)补全条形统计图与扇形统计图．
(3)在扇形统计图中，表示“C”所在的扇形圆心角的度数为______°.
(4)从以上统计图中你能得出什么结论？说说你的想法.(写出一条即可)
24.(本小题10分)
某剧院的观众席的座位为扇形，且按下列分式设置：
(1)按照上表所示的规律，当x每增加1时，y如何变化？
(2)写出座位数y与排数x之间的关系式；
(3)按照上表所示的规律，某一排可能有90个座位吗？说说你的理由．
25.(本小题10分)
小明从家出发骑自行车去上学，当他以往常的速度骑了一段路后，突然想起要买文具，于是又折回到刚经过的某文具店，买到文具后继续骑车去学校，如图是他本次上学所用的时间与离家的距离之间的关系图，根据图中提供的信息回答下列问题：

(1)小明家到学校的距离是______米，文具店到学校的距离是______米；
(2)小明在文具店停留了______分钟，本次上学途中，小明一共行驶了______米；
(3)在整个上学途中，哪个时间段小明骑车速度最快？最快的速度是多少？
(4)如图小明不买文具，以往常的速度去学校，需要花费多长时间？
26.(本小题12分)
如图，在直角坐标平面内，已知点A的坐标为(−3,−3)，点B的坐标为(−3,4)，点P为直线AB上任意一点(不与A、B重合)，点Q是点P关于x轴的对称点．
(1)请求出△ABO的面积．
(2)若点P的纵坐标为n，那么点Q的坐标为______．
(3)若△OPA是△OPQ的面积2倍时，请求出此时P点坐标．
答案和解析
1.【答案】C
【解析】解：由题意得：
x−4≥0，
解得：x≥4，
故选：C．
根据二次根式 a(a≥0)可得x−4≥0，然后进行计算即可解答．
本题考查了函数自变量的取值范围，熟练掌握二次根式 a(a≥0)是解题的关键．
2.【答案】B
【解析】解：A、总体是26000名学生的身高情况，故A不符合题意；
B、1300名学生的身高是总体的一个样本，故B符合题意；
C、样本容量是1300，故C不符合题意；
D、该调查是抽样调查，故D不符合题意．
故选：B．
根据总体、个体、样本，样本的容量以及全面调查和抽样调查的定义求解即可．
本题考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．
3.【答案】D
【解析】解：某辆速度为v(km/h)的车从甲地开往相距s(km)的乙地，全程所用的时间为t(h)，在这个变化过程中，
速度为v(km/h)与所用的时间为t(h)是变量，甲乙两地的距离s(km)是常量，
故选：D．
根据常量、变量的定义结合具体问题情境进行判断即可．
本题考查常量与变量，理解常量与变量的定义是正确判断的前提．
4.【答案】A
【解析】解：根据函数的定义可知，每给定自变量x一个值都有唯一的函数值y相对应，
所以B、C、D错误．
故选：A．
函数就是在一个变化过程中有两个变量x，y，当给x一个值时，y有唯一的值与其对应，就说y是x的函数，x是自变量．注意“y有唯一的值与其对应”对图象的影响．
主要考查了函数图象的读图能力．要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．函数的意义反映在图象上简单的判断方法是：做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点．
5.【答案】C
【解析】解：点P(3,−4)到x轴的距离是：|−4|=4．
故选：C．
直接利用点到x轴的距离即为纵坐标的绝对值，即可得出答案．
此题主要考查了点的坐标，正确掌握点的坐标性质是解题关键．
6.【答案】C
【解析】解：根据题意，得b=a(1+8.5%)(1+9.4%)，
故选：C．
根据2021年荔枝产量比2020年增长8.5%，2022年比2021年增长了9.4%，即可确定b和a的函数关系式．
本题考查了函数关系式，理解题意是解题的关键．
7.【答案】B
【解析】解：建立平面直角坐标系如图，
，
所以嘉嘉放的位置是(1,1)．
故选：B．
首先根据题意建立坐标系，然后再确定根据轴对称图形的定义确定位置
此题主要考查了轴对称图形，关键是掌握如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．
8.【答案】D
【解析】解：由图象可知：
第7周销量最高，是3500个，故选项A不合题意；
第1周到第4周，周销量y(个)随时间t(周)的增大而增大，故选项B不合题意；
第3周和第5周的销量一样，故选项C不符合题意；
在这7周中，周销量增长速度最快的是第2周到第3周和第5周到第6周，故选项D符合题意．
故选：D．
根据图象逐项分析即可．
本题考查了函数图象，观察函数图象的纵坐标得出销量，观察函数图象的横坐标得出第几周，利用数形结合的方法是解答本题的关键．
9.【答案】A
【解析】解：如图：
∵顶点M、N的坐标分别为(3,9)、(12,9)，
∴MN/​/x轴，MN=9，BN/​/y轴，
∴正方形的边长为3，
∴BN=6，
∴B(12,3)
∵AB//MN，
∴AB/​/x轴，
∴A(15,3)，
故选：A．
由图形可得MN/​/x轴，MN=9，BN/​/y轴，可求正方形的边长，即可求解．
本题主要考查了坐标与图形，正确求出点B的坐标是本题的关键．
10.【答案】C
【解析】解：设从甲地到乙地的路程最多有x千米，
根据题意得：10+2(x−3)=22，
解得：x=9，
∴从甲地到乙地的路程最多有9千米．
故选：C．
设从甲地到乙地的路程最多有x千米，利用车费=起步价+2×超过3千米的部分，可列出关于x的一元一次方程，解之即可得出结论．
本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．
11.【答案】B
【解析】解：如图，观察图象可知，C(4,−1)．
故选：B．
利用图象法，画出图象可得结论．
本题考查坐标与图形变化−旋转，解题的关键是正确作出图形，属于中考常考题型．
12.【答案】B
【解析】解：在扇形统计图中，频数“6”对应的圆心角等于360°×640=54°，
故选：B．
用360°乘以频数6占总数的比例即可得．
本题主要考查扇形统计图与频数(率)分布直方图，解题的关键是掌握扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数．通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系．
13.【答案】C
【解析】解：把A点和直线x=1，向左移动1个单位得：A′(3,3)和直线x=0，
点A′(3,3)关于x=0的对称点为B(−3,3)，
把B(−3,3)再向右平移1个单位得：(−2,3)，
故选：C．
先把A点和直线x=1，向左移动1个单位，求出关于y轴的对称点，再向右平移1个单位．
本题考查了坐标与图形的变化，掌握平移的特征是解题的关键．
14.【答案】C
【解析】解：第1个图案有4个三角形，即4=3×1+1
第2个图案有7个三角形，即7=3×2+1
第3个图案有10个三角形，即10=3×3+1
…
按此规律摆下去，
第n个图案有(3n+1)个三角形．
故选：C．
根据图形的变化发现规律，即可用含n的代数式表示．
本题考查了规律型−图形的变化类、列代数式，解决本题的关键是根据图形的变化寻找规律．
15.【答案】C
【解析】解：A.随着氮肥施用量的增大，土豆产量先是逐渐的增加，然后又逐渐减少，因此选项A不符合题意；
B.氮肥施用量是101kg时，土豆产量大约为32.29t，因此选项B不符合题意；
C.如果不施氮肥，土豆的产量是15.18吨/公顷，故此选项正确，符合题意；
D.土豆产量为39.45t时，氮肥的施用量为202kg或471kg，因此选项D不符合题意．
故选：C．
从表格中的变量之间的变化关系以及对应值逐项进行判断即可．
本题考查函数及其表示方法，理解函数的意义及其变化关系是解题的关键．
16.【答案】A
【解析】解：当x=−1时，y=−3+b，当x=5时，y=6−5=1，
由题意得：−3+b=1，
解得：b=4，
故选：A．
把x=−1与x=5代入程序中计算，根据y值相等即可求出b的值．
此题考查了函数值，弄清程序中的关系式是解本题的关键．
17.【答案】(2,1)
【解析】解：∵点M(−4,1)，先向右平移2个单位得(−2,1)，
∴点(−2,1)关于y轴对称的坐标为(2,1)．
故答案为：(2,1)．
先求出平移后的坐标，再利用关于y轴对称点的性质得出答案．
此题主要考查了关于y轴对称点的性质和平移规律，正确把握横纵坐标的关系是解题关键．
18.【答案】33 2019
【解析】解：由条形统计图可得：该市2020年私人汽车拥有量比前一年增加了183−150=33(万辆)，
由折线统计图可得，私人汽车拥有量年增长率最大的是：2019年．
故答案为：33，2019．
根据条形统计图的数据可得该市2020年私人汽车拥有量比前一年增加的数量，根据折线统计图可得私人汽车拥有量年增长率最大的年份．
此题主要考查了折线统计图以及条形统计图的应用，正确利用图形获取信息是解题关键．
19.【答案】3 2 20
【解析】解：(1)24÷8=3(吨/分)，
设每分钟的出油量为x吨，
(3−x)(24−8)=40−24，
16(3−x)=16，
3−x=1，
x=2，
故答案为3，2；
(2)解：40÷2=20(分钟)，
故答案为：20．
(1)根据图象得，每分钟的进油量为：24÷8=3，设每分钟的出油量为x吨，(3−x)(24−8)=40−24，进行计算即可得；
(2)由(1)得每分钟的出油量为2吨，即可得．
本题考查了函数的图象，解题的关键是理解题意，能够根据函数图象得到相应的信息．
20.【答案】高中楼
【解析】解：(1)如图所示：校门的坐标为(1,−3)；
故答案为：高中楼，坐标系见解析；
(2)由图可得，校门(1,−3)，图书馆(4,1)操场(1,3)．
(1)直接利用已知点坐标得出原点位置，进而建立平面直角坐标系得出答案；
(2)直接利用平面直角坐标系得出食堂的位置．
本题主要考查了坐标确定位置，正确得出原点位置是解题关键．
21.【答案】解：(1)∵长方形的周长为40，
∴2(x+y)=40，
∴y=20−x；
(2)当x=12时，y=20−12=8，
∴长方形的面积为12×8=96．
【解析】(1)根据题意得2(x+y)=40，进行计算即可得；
(2)当x=12时，代入函数表达式即可得．
本题考查了一次函数的应用，解题的关键是理解题意，掌握一次函数的性质．
22.【答案】解：(1)∵M(m−1,2m+4)在y轴上，
∴m−1=0，
解得：m=1；
(2)∵点M在二、四象限的角平分线上，
∴m−1=−2m−4，
∴m=−1，
所以M(−2,2)．
【解析】(1)若点在y轴上，则M的横坐标为0，即m−1=0；
(2)若点M在第二、四象限的角平分线上，则点M的横纵坐标互为相反数，即m−1=−2m−3．
本题考查的知识点是象限及点坐标的特点，掌握以上知识点是解题的关键．
23.【答案】72
【解析】解：(1)∵由十分了解的有34人，占17%，
∴被调查的学生总人数共有：34÷17%=200(人)；
(2)了解较少的人数有：200−55−40−34=71，“了解较多”部分所占的比例为：40200×100%=20%，
补全条形统计图：
(3)扇形统计图中“C”所在的扇形圆心角的度数为：360°×40200=72°，
故答案为：72；
(4)十分了解卡塔尔世界杯的人数占比太小(答案不唯一)．
(1)由十分了解的有34人，占17%，可求得接受问卷调查的学生数；
(2)求了解较少的人数及“了解较多”部分所占的比例，继而补全条形统计图；
(3)由360°乘以扇形统计图中“了解较多”部分所占的比例即可得出“C”所在的扇形圆心角的度数；
(4)十分了解卡塔尔世界杯的人数占比太小．
本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
24.【答案】解：(1)由图表中数据可得：当x每增加1时，y增加3；
(2)由题意可得：y=50+3(x−1)=3x+47；
(3)某一排不可能有90个座位，
理由：由题意可得：y=3x+47=90，
解得：x=433．
故x不是整数，则某一排不可能有90个座位．
【解析】本题主要考查了函数关系，正确得出y与x的函数关系式是解题关键．
(1)根据表格中数据直接得出y的变化情况；
(2)根据x，y的变化规律得出y与x的函数关系；
(3)利用(2)中所求，将y=90代入分析即可．
25.【答案】1500 900 4 2700
【解析】解：(1)由题意可知，小明家到学校的距离是1500米，
1500−600=900(米)．
即文具店到学校的距离是900米．
故答案为：1500；900；
(2)12−8=4(分钟)．
故小明在文具店停留了4分钟．
1200+(1200−600)+(1500−600)=2700(米)．
故本次上学途中，小明一共行驶了2700米，
故答案为：4；2700；
(3)根据题中图象，可知第12分钟至第14分钟这一时间段的线段最陡，所以小明在第12分钟至第14分钟这一时间段的骑车速度最快，
此时速度为1500−60014−12=450(米/分)．
答：在整个上学途中，第12分钟至第14分钟这一时间段的骑车速度最快，最快速度为450米/分；
(4)小明往常的速度为1200÷6=200(米/分)，
去学校需要花费的时间为1500÷200=7.5(分钟)．
答：小明不买文具，以往常的速度去学校，需要花费7.5分钟．
(1)根据函数图象的纵坐标，可得答案；
(2)根据函数图象的横坐标，可得到达文具店时间，离开文具店时间，根据有理数的减法，可得答案，根据函数图象的纵坐标，可得相应的路程，根据有理数的加法，可得答案；
(3)根据函数图象的纵坐标，可得路程，根据函数图象的横坐标，可得时间，根据路程与时间的关系，可得速度；
(4)根据路程、速度，即可得到时间．
本题考查利用函数的图象解决实际问题，正确理解函数图象横纵坐标表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．需注意计算单位的统一．
26.【答案】(−3,−n)
【解析】解：(1)∵A的坐标为(−3,−3)，点B的坐标为(−3,4)，
∴AB=4−(−3)=4+3=7，
∴S△ABO=12×7×3=10.5；
(2)∵P为直线AB上任意一点，点P的纵坐标为n，点Q是点P关于x轴的对称点，
∴P(−3,n)，
则点Q的坐标为(−3,−n)；
故答案为：(−3,−n)；
(3)∵△OPA是△OPQ面积2倍，点O到直线AB的距离都是3，
∴AP=2PQ，
此时点P的坐标为(−3,n)，则点Q坐标为(−3,−n)，
当点P在x轴的下方时，
则有n−(−3)=2(−n−n)，
解得n=−35，
则P坐标为(−3,−35)；
当点P在x轴的上方时，
则有n+3=2[n−(−n)]，
解得n=1，
则P坐标为(−3,1)；
综上所述，点P的坐标为(−3,−35)或(−3,1)．
(1)根据三角形的面积公式进行解答；
(2)关于x轴对称的点的横坐标相等，纵坐标互为相反数；
(3)分类讨论：①点P在x轴的下方；②点P在x轴的上方．
本题考查了关于x、y轴对称的点的坐标特征，三角形的面积公式以及坐标与图形变换．注意“数形结合”数学思想的应用．氮肥施用量/kg
0
34
67
101
135
202
259
336
404
471
土豆产量/t
15.18
21.36
25.72
32.29
34.03
39.45
43.15
43.46
40.83
39.45
排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…