中职高教版（2021·十四五）4.7 余弦函数的图像和性质优质课练习题习题ppt课件

这是一份中职高教版（2021·十四五）4.7 余弦函数的图像和性质优质课练习题习题ppt课件，文件包含47余弦函数的图像和性质课件pptx、47余弦函数的图像和性质教案docx、47余弦函数的图像和性质课内习题答案docx等3份课件配套教学资源，其中PPT共22页， 欢迎下载使用。

4.7 余弦函数的图像和性质
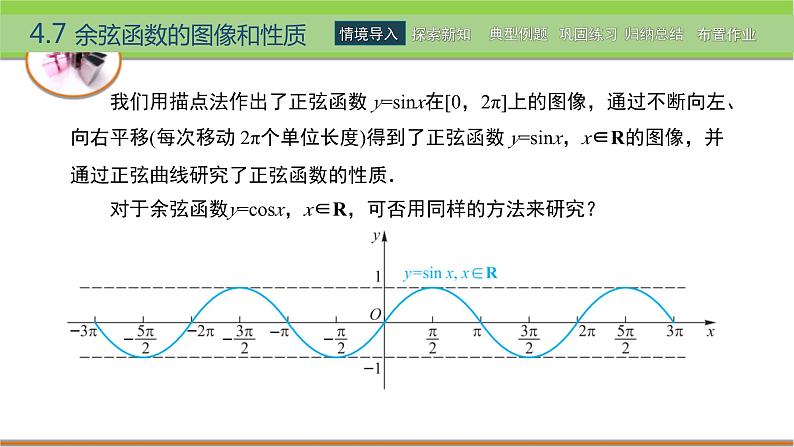
我们用描点法作出了正弦函数 y=sinx在[0，2π]上的图像，通过不断向左、向右平移(每次移动 2π个单位长度)得到了正弦函数 y=sinx，x∈R的图像，并通过正弦曲线研究了正弦函数的性质． 对于余弦函数y=csx，x∈R，可否用同样的方法来研究？
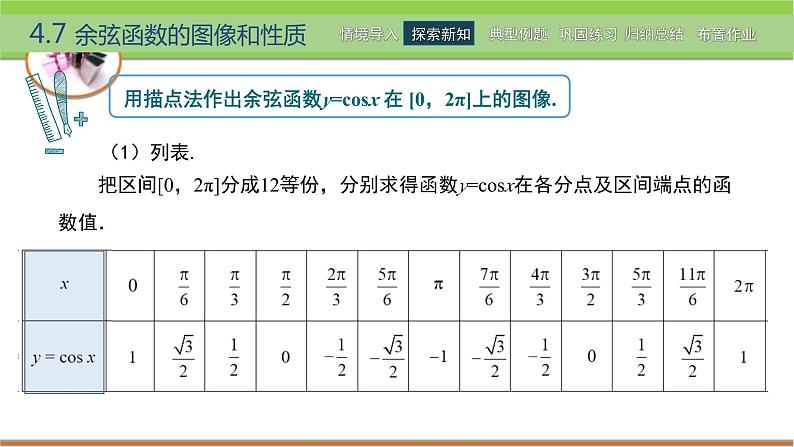
把区间[0，2π]分成12等份，分别求得函数y=csx在各分点及区间端点的函数值．
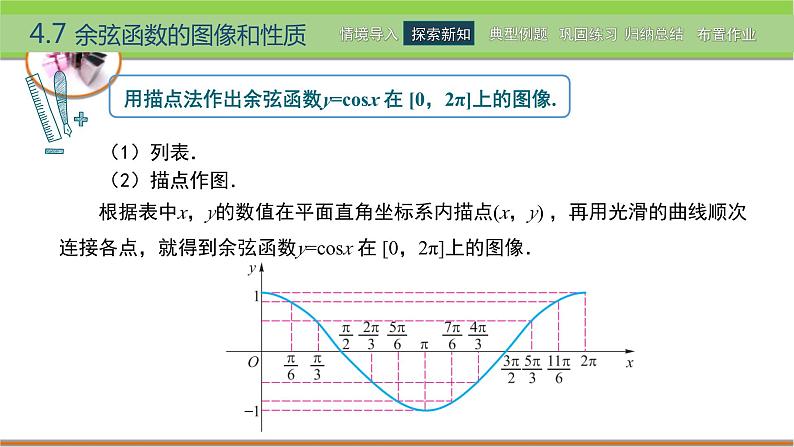
根据表中x，y的数值在平面直角坐标系内描点(x，y) ，再用光滑的曲线顺次连接各点，就得到余弦函数y=csx 在 [0，2π]上的图像．
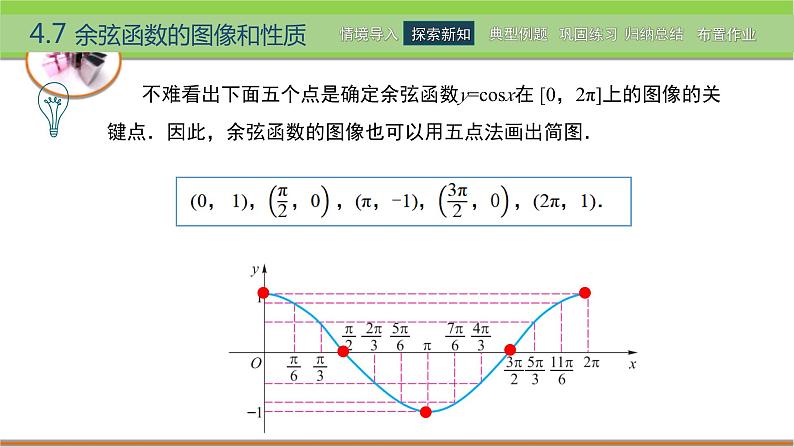
不难看出下面五个点是确定余弦函数y=csx在 [0，2π]上的图像的关键点．因此，余弦函数的图像也可以用五点法画出简图．
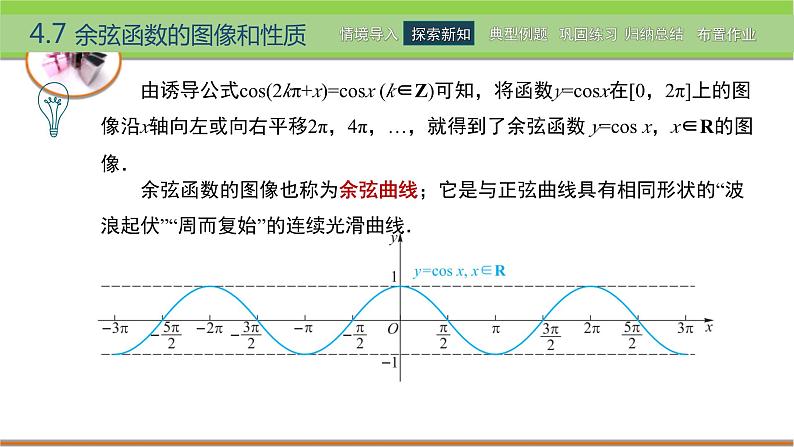
由诱导公式cs(2kπ+x)=csx (k∈Z)可知，将函数y=csx在[0，2π]上的图像沿x轴向左或向右平移2π，4π，…，就得到了余弦函数 y=cs x，x∈R的图像．
余弦函数的图像也称为余弦曲线；它是与正弦曲线具有相同形状的“波浪起伏”“周而复始”的连续光滑曲线．
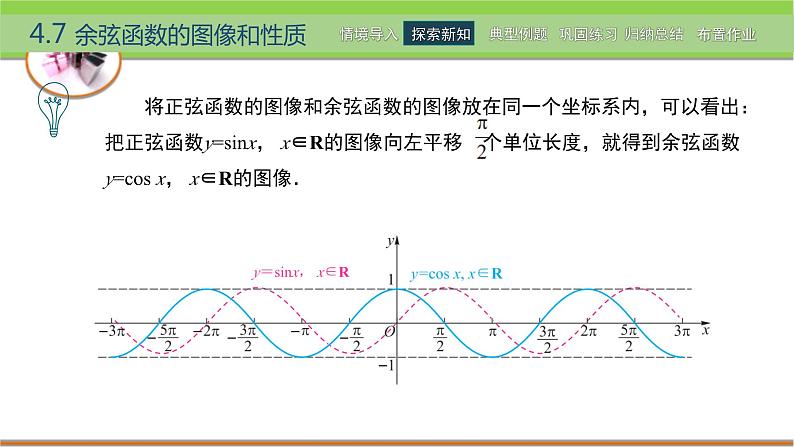
若将正弦函数y=sinx，x∈R的图像向右平移，是否也可以得到余弦函数y=cs x，x∈R的图像，如果是，需平移多少？
（1）定义域．
观察余弦曲线，类比正弦函数，得到关于余弦函数y=csx，x∈R的结论：
余弦函数的定义域是实数集R ．
（2）值域．
余弦函数的值域是[-1，1] ．当x=2kπ(k∈Z)时，y取最大值，ymax=1；当x=π+2kπ(k∈Z)时，y取最小值，ymin= -1 ．
（3）周期性．
余弦函数是周期为2π的周期函数．
（4）奇偶性．
由图像关于y轴对称和诱导公式cs(−x)=csx可知，余弦函数是偶函数．
余弦函数y=csx在每一个闭区间[(2k-1)π， 2kπ] (k∈Z) 上都是增函数，函数值从-1增大到1；在每一个闭区间[2kπ，(2k+1)π] (k∈Z)上是减函数，函数值从1减小到-1．
（5）单调性．
例1 利用五点法作出函数y=-csx在[0，2π]上的图像．
（2）描点作图．根据表中x，y的数值在平面直角坐标系内描点(x，y)，再用平滑曲线顺次连接各点，就得到函数y=-csx在[0，2π]上的图像．
例1 利用五点法作出函数y=-csx在[0，2π]上的图像．
例2 求函数y=3csx＋1的最大值、最小值及取得最大值、最小值时x的集合．
解 由余弦函数的性质知，-1≤csx≤1，所以-3≤3csx≤3，从而 -2≤3csx+1≤4，即 -2≤y≤4 ． 故函数的最大值为4，最小值为-2 ．
函数y=3csx+1取最大值时的x的集合，就是函数y=csx取得最大值时的x的集合 {x|x=2kπ， k∈Z}； 函数y=3csx + 1取最小值时的x的集合，就是函数y=csx取得最小值时的x的集合 {x|x=2kπ+π， k∈Z}．
解 根据余弦函数的图像和性质可知：
1. 用五点法作出函数y=csx-1在[0， 2π]上的图像．
3. 不求值，比较下列各组数的大小．