四川省达州市开江中学2022-2023学年九年级下学期5月月考数学试卷(含答案)

这是一份四川省达州市开江中学2022-2023学年九年级下学期5月月考数学试卷(含答案)，共19页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．如图，一次函数y＝2x+3与y轴相交于点A，与x轴相交于点B，在直线AB上取一点P（点P不与A，B重合），过点P作PQ⊥x轴，垂足为点Q，连接PO，若△PQO的面积恰好为，则满足条件的P点有( )
A.1个B.2个C.3个D.4个
2．如图，四边形是的内接四边形，其中，则的度数为( )
A.B.C.D.
3．下列四组数能作为直角三角形三边长的是( )
A.，，B.，，
C.，，D.，，
4．下列给出的四组数中，能构成直角三角形三边的一组是( )
A.5，12，14B.6，8，9C.7，24，25D.8，13，15
5．将方程4x+3=6x+7移项后正确的是( )
A.4x-6x=7+3B.4x-6x=7-3C.6x-4x=3+7D.6x-4x=7-3
6．如图，在Rt△ABC中，∠B＝90°，AB＝8，BC＝6，延长BC至E，使得CE＝BC，将△ABC沿AC翻折，使点B落点D处，连接DE，则DE的长为( )
A.B.C.D.
7．已知物体下落高度h关于下落时间t的函数关系式h＝gt2，则此函数的图象为( )
A.B.C.D.
8．若是关于的一元二次方程的一个解，则的值是( )
A.4B.3C.2D.1
9．若一个三角形的两边长分别为5和10则第三边长可能是( )
A.5B.6C.15D.16
10．下列说法正确的是( )
A.在等式ab＝ac两边除以a，可得b＝c
B.在等式2x＝2a﹣b两边除以2，可得x＝a﹣b
C.在等式a＝b两边除以（c2+1），可得＝
D.在等式两边除以a，可得b＝c
二、填空题
11．如图，AB是⊙O的直径，点C在⊙O上（点C不与A、B重合），过点C作⊙O的切线交AB的延长线于点D，连结AC.若∠A=25°，则∠D的度数是______°.
12．甲列车从A地开往B地，速度是60km/h，乙列车同时从B地开往A地，速度是90km/h.已知AB两地相距200km，则两车相遇的地方离A地______km.
13．双曲线经过点，则______ (填“”，“”或“”).
14．方程x2+2x–2=0配方得到（x+m）2=3，则m=______.
15．已知：如图，在矩形ABCD中，CE⊥BD，E为垂足，∠DCE：∠ECB=3：1，则∠ACE=______.
16．如图，二次函数的图象开口向上，图象经过点和，且与轴相交于负半轴，给出五个结论：①；②；③；④；⑤.其中正确结论的序号是______.
三、解答题
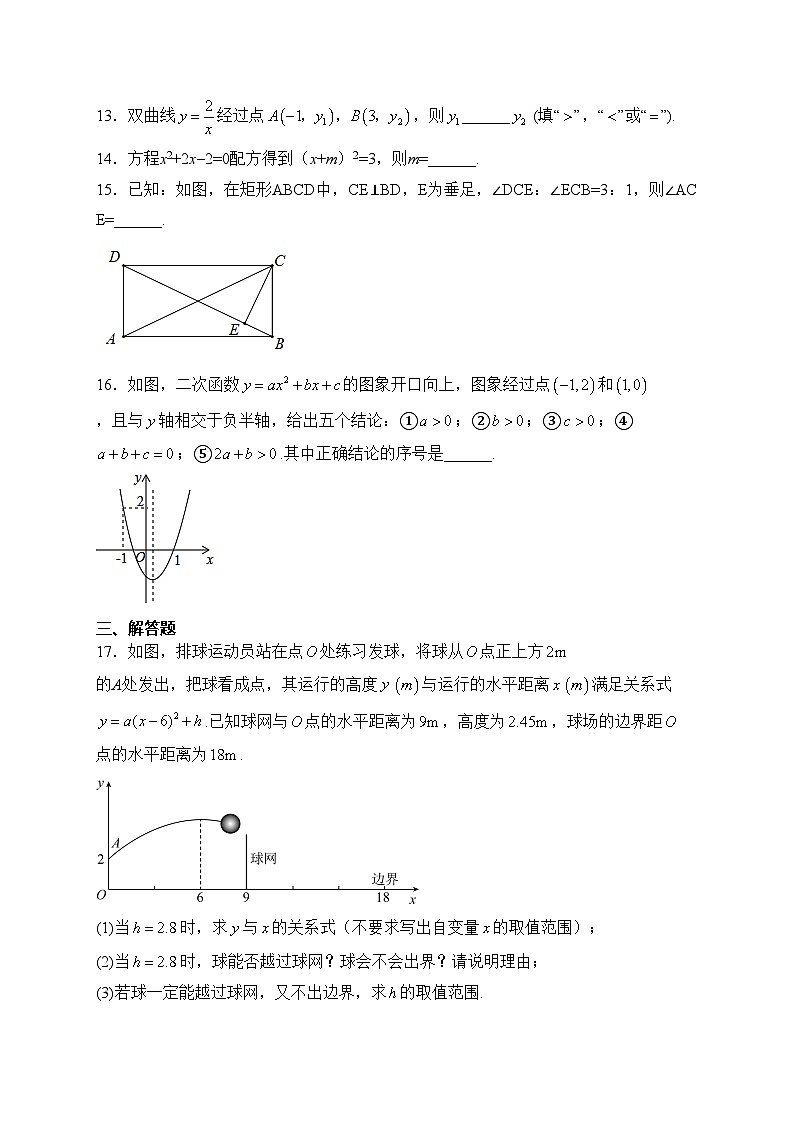
17．如图，排球运动员站在点处练习发球，将球从点正上方的A处发出，把球看成点，其运行的高度与运行的水平距离满足关系式.已知球网与点的水平距离为，高度为，球场的边界距点的水平距离为.
(1)当时，求与的关系式（不要求写出自变量的取值范围）；
(2)当时，球能否越过球网？球会不会出界？请说明理由；
(3)若球一定能越过球网，又不出边界，求的取值范围.
18．已知：如图，为直径，、是的切线，A、C为切点，.
（1）求的大小；
（2）若，求的长.
19．综合与探究：如图，抛物线（）与轴交于点和点，与轴交于点.
(1)求此抛物线的函数表达式；
(2)若点是第三象限抛物线上一动点，连接，，，求面积的最大值，并求出此时点的坐标；
(3)若点在抛物线的对称轴上，线段绕点逆时针旋转90°后，点的对应点恰好也落在此抛物线上，请直接写出点的坐标.
20．计算：
21．
22．运用适当的方法解方程
（1）；
（2）.
23．如图，抛物线与坐标轴交于，两点，直线与抛物线交于，两点，已知点坐标为.
(1)求二次函数和一次函数解析式；
(2)求出点坐标，并结合图象直接写出不等式的解集；
(3)点是直线上的一个动点，将点向上平移2个单位长度得到点，若线段与抛物线有公共点，请直接写出点的横坐标的取值范围.
24．如图，在平面直角坐标系中，网格图中的小方格都是边长为1个单位长度的小正方形，的三个顶点都在格点上.
(1)分别写出A、B、C三点的坐标；
(2)将各个顶点坐标都乘2，在平面直角坐标系中画出放大后的；
(3)直接写出两个三角形的面积关系：______.
25．小明家住深圳某小区一楼，家里开了一间小卖部，小明的爸爸想把囤积的商品打折促销7天，因为考虑到疫情期间的安全问题，小明爸爸把一楼朝南的窗户改造成了营业窗口，如下图1，因为天气渐渐回暖，小明的爸爸想让小明帮忙设计一个可以伸缩的遮阳棚，如图2，AB表示窗户，高度为2米，宽度为3米，BCD表示直角遮阳篷，他打算选择的支架BC的高度为0.5米.小明为了最大限度地阻挡正午最强的阳光，为了测量太阳与地面的最大夹角，小明选择一个晴朗的天气，正午12点时在地面上竖立了一个长4米的木杆，测得落在地面的影子长为2.31米.参考数据（tan60°=≈1.73）
(1)正午12点时，太阳光线与地面的夹角约为________度，请你帮忙估算出没有遮阳棚时，正午12点时太阳照射到室内区域面积为___________.（结果保留根号）
(2)正午12点时，太阳刚好没有射入室内，求此时CD的长.（结果保留根号）.
参考答案
1．答案：C
解析：∵点P在直线AB上，
∴设P（m，2m+3），
①当P点在第一象限时，
，
∴2m2+3m＝，
2m2+3m﹣=0，
Δ＝18＞0，
x＝，
m1＝，m2＝，
∵P点在第一象限，
∴P（，）
②当P点在第二象限时，
∴，
∴，
2m2+3m+＝0，
Δ＝0，
m＝﹣＜0，
∴P（﹣，）；
③当P点在第三象限时，
解得m1＝，m2＝，
∵P点在第三象限，
∴P（，），
综上所述：P（，）或P（，）或P（﹣，）.
故选：C.
2．答案：C
解析：∵四边形为圆内接四边形，
∴，
∵，
∴.
故选：C.
3．答案：A
解析：A、因为，则以、、为三边的三角形为直角三角形，所以A选项符合题意；
B、因为，则以、、为三边的三角形不是直角三角形，所以B选项不符合题意；
C、因为，则以、、为三边的三角形不是直角三角形，所以C选项不符合题意；
D、因为，，，因为，则以、、为三边的三角形不是直角三角形，所以D选项不符合题意，
故选：A.
4．答案：C
解析：A、，不能构成直角三角形，故此选项不符合题意；
B、，不能构成直角三角形，故此选项不符合题意；
C、，能构成直角三角形，故此选项符合题意；
D、，不能构成直角三角形，故此选项不符合题意；
故选：C.
5．答案：B
解析：A、4x-6x=7+3，3移动后没改变符号，故不正确，
B、4x-6x=7-3，移动的两项6x与3都改变了符号，故正确，
C、6x-4x=3+7，移动的两项6x与3都没改变了符号，而未移动的项4x却变了符号，故不正确，
D、6x-4x=7-3，移动的两项6x没改变了符号，3都改变了符号，而未移动的项4x也变了符号，故不正确.
6．答案：D
解析：连接BD交AC于点F，
∵将△ABC沿AC翻折，使点B落点D处，
∴AB=AD，CB=CD，∠BAC=∠DAC，
∴BF=DF，∠BFC=90°，
∵AB=8，BC=6，
∴AC=，



∵CE=BC，
所以CD=CB=CE，


即

故选：D.
7．答案：A
解析：∵g表示的是重力加速度；
∴g为正常数；
∴h=×g×t2(其中g为正常数)为二次函数,其图象为抛物线；
∵×g＞0；
∴抛物线开口向上；
∵t≥0；
∴h=×g×t2(其中g为正常数)的图象只是抛物线在第一象限的部分；
故选A.
8．答案：A
解析：把代入得：
故选A.
9．答案：B
解析：∵一个三角形的两边长分别为5和10，
∴10-5＜第三边＜5+10，即5＜第三边＜15，
故选：B.
10．答案：C
解析：A、当a＝0时，该结论不成立，故A错误.
B、在等式2x＝2a﹣b两边除以2，可得，故B错误.
C、由于c2+1＞1，在等式a＝b两边除以（c2+1），可得，故C正确.
D、在等式两边除以a，可得，故D错误.
故选：C.
11．答案：40
解析：连接OC.
∵OA=OC，
∴∠A=∠OCA=25°.
∴∠DOC=∠A+∠ACO=50°.
∵CD是的切线，
∴∠OCD=90°.
∴∠D=180°−90°−50°=40°.
12．答案：80
解析：设两车相遇的时间为x小时，
根据题意得：（60+90）x=200，
解得：x=，
∴60x=60×=80.
故两车相遇的地方离A地80km.
故答案为80.
13．答案：
解析：∵双曲线的图象在第一、三象限，经过点，
∴，
∴，
故答案为：.
14．答案：1
解析：


故答案为1.
15．答案：45°
解析：∵四边形ABCD是矩形，
∴∠DCB=90°，
∵∠DCE：∠ECB=3：1，
∴∠DCE=×90°=67.5°，∠ECB=22.5°
∴∠EBC=∠ACB=90°-∠ECB=67.5°
∴∠ACE=∠ACB-∠ECB=67.5°-22.5°=45°.
16．答案：①④⑤
解析：①由抛物线的开口方向向上可推出a＞0，正确；
②因为对称轴在y轴右侧，对称轴为x=＞0，又因为a＞0，
∴b＜0，错误；
③由抛物线与y轴的交点在y轴的负半轴上，
∴c＜0，错误；
④由图象可知：当x=1时y=0，
∴a+b+c=0，正确；
⑤由图象可知：对称轴x=＞0且对称轴x=＜1，
∴2a+b＞0，正确；
故答案为：①④⑤.
17．答案：(1)y与x的关系式为：
(2)当时，球能越过球网；当时，球不会出界，理由见解析
(3)若球一定能越过球网，又不出边界，h的取值范围是：
解析：（1）由图象可知：点A的坐标为
将点和代入解析式中，得
,解得：
∴与的关系式为.
（2）球能越过球网，球不会出界，理由如下
将代入中，得
，
∴球能越过球网；
将代入中，得
，
∴该抛物线与x轴的右交点必在（18，0）的左侧，
∴球不会出界，
综上：球能越过球网，球不会出界.
（3）将点代入解析式中，得：
解得：
∴抛物线的解析式为
若球一定能越过球网，则当时， ；
∴，解得：
若不出边界，即抛物线与x轴的右交点在的左侧或重合，即当时，；
∴，解得
综上：若球一定能越过球网，又不出边界，h的取值范围为.
18．答案：（1）
（2）
解析：（1）∵，是的切线
∴，
∴
∴
（2）连接，如图所示：
∵为的直径
∴
∵
∴
∴
∵，
∴为等边三角形
∴.
19．答案：(1)抛物线的函数表达式
(2)当时，S有最大值为，此时
(3)，
解析：（1）()与轴交于点和点两点，
，
解得：，
抛物线的解析式为：
（2）令，
点的坐标为，又，
直线的解析式为：，
设点，，过点作轴的垂线，交于点，
则点，
，
，
，
当时，S有最大值为，此时，
（3），
抛物线的对称轴为，
点在抛物线的对称轴上，
设，
线段绕点逆时针旋转90°后，点的对应点恰好也落在此抛物线上，
分两种情况：
①，要使,由二次函数的对称性可知点与点重合，
设抛物线对称轴与x轴相交于点,
由为等腰直角三角形，
，
，
②，由题意，得，
如图，过点作于点，
易证≌，
，
，
代入得到，
解得：（舍），
，
综上满足条件的点，
20．答案：1
解析：
=
=2-1+2-2
=1.
21．答案：
解析：移项得：，
提公因式得：.
∴或.
∴.
22．答案：（1）
（2）
解析：（1），
，
，
解得：；
（2），
，
，
，
解得：.
23．答案：(1)，
(2)，
(3)或
解析：（1）将点B的坐标分别代入两个函数表达式得：
，解得：，
故二次函数和一次函数的表达式分别为：，；
（2）联立一次函数和二次函数表达式得：，
解得：或，
即点，
观察函数图象知，不等式的解集为：；
（3）如图，当点恰好在抛物线上时，由点向上平移2个单位长度得到点，可知，即，
解得：或1，
由图象可知，线段与抛物线有公共点，点的横坐标为：或.
24．答案：(1)，，
(2)见解析
(3)4
解析：（1）根据直角坐标系中的图形可知，，，
（2）点，，，
根据题意由：点，，
如图，，
即为所求；
（3）∵，，，
∴，，轴，轴，
∴的面积为：，
∵，，，
∴，，轴，轴，
∴的面积为：，
∴，
故答案为4.
25．答案：(1)60°，
(2)
解析：（1）设正午12点时，太阳光线与地面的夹角为，由题意可知∶
，
，
正午12点时，太阳光线与地面的夹角约为
由题意可知：没有遮阳棚时，正午12点时太阳照射到室内区域面积为∶
没有遮阳棚时，正午12点时太阳照射到室内区域面积为，
故答案为：；
（2）由题意可知∶
，
，
，
，
，
此时的长为.