四川省成都市青羊区树德中学2022—2023学年下学期3月月考九年级数学试卷（含答案）

这是一份四川省成都市青羊区树德中学2022—2023学年下学期3月月考九年级数学试卷（含答案），共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（4分）的倒数是（ ）
A．B．﹣5C．D．5
2．（4分）疫情管控放开，旅游业触底反弹，文旅消费需求剧增．据四川省文化和旅游厅消息，2023年春主假日期间，四川省共接待游客5387.59万人次，居全国第一，实现旅游收入242.16亿元．其中数据5387.59万用科学记数法可表示为（ ）
A．5.38759×103B．5.38759×104
C．5.38759×106D．5.38759×107
3．（4分）若x≠y，下列分式化简正确的是（ ）
A．B．C．D．
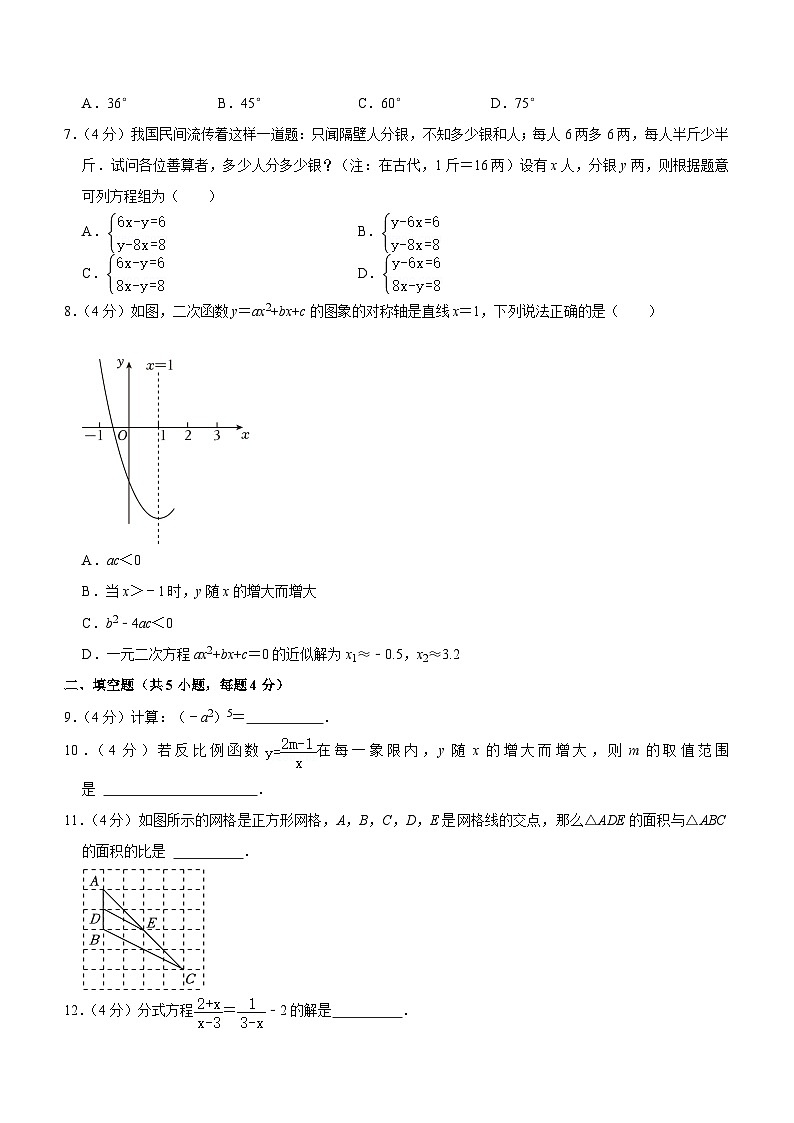
4．（4分）如图，在△ABC和△DCB中，∠ABC＝∠DCB，只添加一个条件能判定△ABC≌△DCB的是（ ）
A．BC＝CBB．AC＝BDC．AB＝CDD．∠ABC＝∠D
5．（4分）某班为了解学生对党史的学习情况，随机抽取了8名学生进行调查，他们读书的本数分别是3、2、3、3、5、1、2、5，则这组数据的中位数是（ ）
A．2B．3C．4D．5
6．（4分）如图，正六边形ABCDEF内接于⊙O，点M在上，则∠CME的度数为（ ）
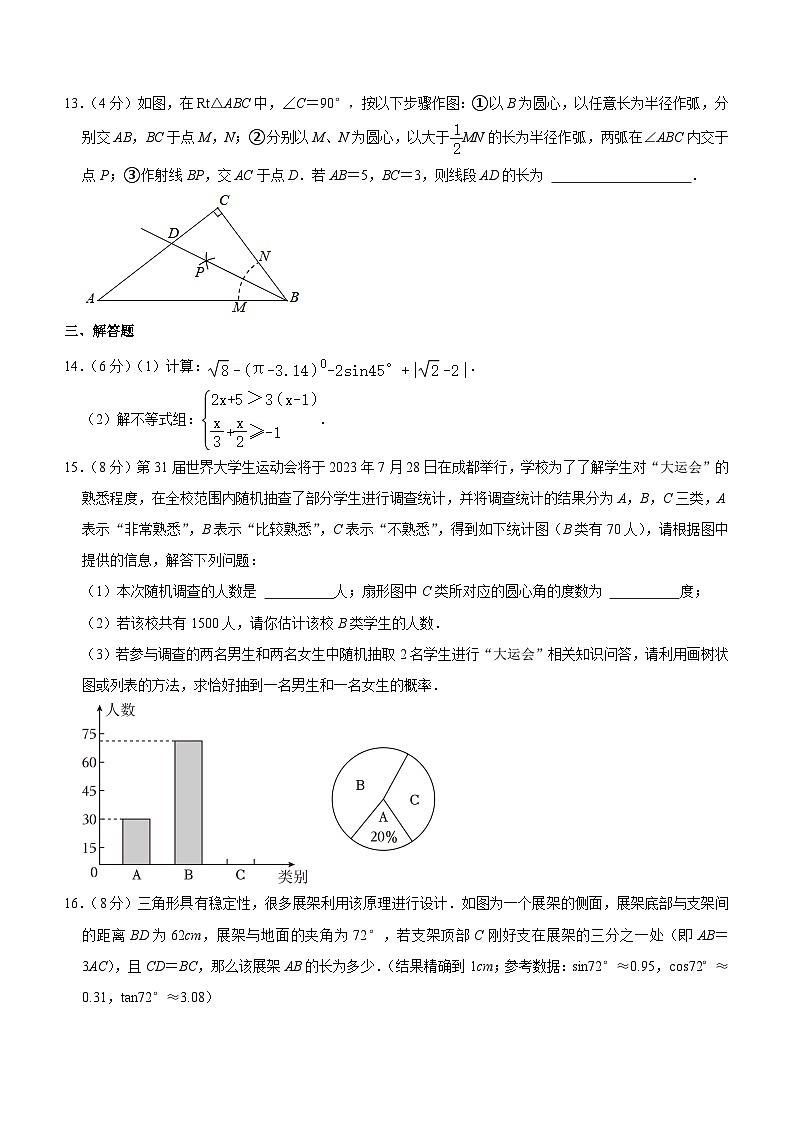
A．36°B．45°C．60°D．75°
7．（4分）我国民间流传着这样一道题：只闻隔壁人分银，不知多少银和人；每人6两多6两，每人半斤少半斤．试问各位善算者，多少人分多少银？（注：在古代，1斤＝16两）设有x人，分银y两，则根据题意可列方程组为（ ）
A．B．
C．D．
8．（4分）如图，二次函数y＝ax2+bx+c的图象的对称轴是直线x＝1，下列说法正确的是（ ）
A．ac＜0
B．当x＞﹣1时，y随x的增大而增大
C．b2﹣4ac＜0
D．一元二次方程ax2+bx+c＝0的近似解为x1≈﹣0.5，x2≈3.2
二、填空题（共5小题，每题4分）
9．（4分）计算：（﹣a2）5＝ ．
10．（4分）若反比例函数在每一象限内，y随x的增大而增大，则m的取值范围是 ．
11．（4分）如图所示的网格是正方形网格，A，B，C，D，E是网格线的交点，那么△ADE的面积与△ABC的面积的比是 ．
12．（4分）分式方程＝﹣2的解是 ．
13．（4分）如图，在Rt△ABC中，∠C＝90°，按以下步骤作图：①以B为圆心，以任意长为半径作弧，分别交AB，BC于点M，N；②分别以M、N为圆心，以大于MN的长为半径作弧，两弧在∠ABC内交于点P；③作射线BP，交AC于点D．若AB＝5，BC＝3，则线段AD的长为 ．
三、解答题
14．（6分）（1）计算：．
（2）解不等式组：．
15．（8分）第31届世界大学生运动会将于2023年7月28日在成都举行，学校为了了解学生对“大运会”的熟悉程度，在全校范围内随机抽查了部分学生进行调查统计，并将调查统计的结果分为A，B，C三类，A表示“非常熟悉”，B表示“比较熟悉”，C表示“不熟悉”，得到如下统计图（B类有70人），请根据图中提供的信息，解答下列问题：
（1）本次随机调查的人数是 人；扇形图中C类所对应的圆心角的度数为 度；
（2）若该校共有1500人，请你估计该校B类学生的人数．
（3）若参与调查的两名男生和两名女生中随机抽取2名学生进行“大运会”相关知识问答，请利用画树状图或列表的方法，求恰好抽到一名男生和一名女生的概率．
16．（8分）三角形具有稳定性，很多展架利用该原理进行设计．如图为一个展架的侧面，展架底部与支架间的距离BD为62cm，展架与地面的夹角为72°，若支架顶部C刚好支在展架的三分之一处（即AB＝3AC），且CD＝BC，那么该展架AB的长为多少．（结果精确到1cm；参考数据：sin72°≈0.95，cs72°≈0.31，tan72°≈3.08）
17．（10分）如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，以CD为直径作⊙O，交BC边于点E，过点E作EF⊥AB，垂足为点F．
（1）求证：EF为⊙O的切线；
（2）若AC＝6，CD＝5，求DF的长．
18．（10分）已知一次函数y1＝x+2与反比例函数y2＝的图象交于A、B两点，交y轴于点C．
（1）当A点的横坐标为4时，求反比例函数的表达式和点B的坐标；
（2）在（1）的条件下，若点A关于原点的对称点为A'，求△AA′B的面积；
（3）探究：点P在y轴上，是否存在一点P，使得△ABP为等腰直角三角形，且直角顶点为点P．若存在，求出P点坐标及此时的k值；若不存在，请说明理由．
一、填空题（共5小题，每小题4分）
19．（4分）已知x2+3x+1＝0，则代数式的值为 ．
20．（4分）如图，平面直角坐标系中一条圆弧经过网格点A，B，C，点A在y轴上，点B的坐标为（4，4），则该圆弧AC的长为 ．
21．（4分）有五张正面分别写有数字﹣4，﹣3，0，2，3的卡片，五张卡片除了数字不同外其余全部相同，现将它们背面朝上，洗匀后从中随机抽取一张，记卡片上的数字为n，则抽取的n既能使关于x的方程x2﹣2（n+1）x+n（n﹣3）＝0有实数根，又能使以x为自变量的二次函数y＝﹣x2+2nx+1，当x＞2时，y随x增大而减小的概率为 ．
22．（4分）在平面直角坐标系中，以P（t，0）为圆心，单位长1为半径的圆与直线y＝kx﹣3相切于点M，直线y＝kx﹣3与x轴交于点A，与y轴交于点N，当MN取得最小值时，点A的坐标为 ．
23．（4分）如图，在平面直角坐标系xOy中，点A的坐标为，点C在函数的图象上，若点A绕点C顺时针旋转120°，所得对应点B刚好落在y轴的正半轴上，则线段AB的长为 ．
二、解答题
24．（8分）晚饭后，小萌和妈妈出门散步，两人同时从家门口出发，小萌骑上新学会的平衡车，骑行3分钟后，他发现妈妈没有跟上，于是立刻掉头，以1.5倍的速度回去接妈妈．妈妈步行的速度是60m/min，小萌与妈妈的距离y（m）与骑行的时间x（min）之间的关系如图所示．
（1）求出AB所在直线的函数关系式；
（2）小萌掉头后多久接到妈妈？
25．（10分）如图，在平面直角坐标系xOy中，直线y＝kx﹣2与抛物线y＝﹣x2+2相交于A，B两点（点A在点B的左侧）．若抛物线y＝﹣x2+2的顶点为C，直线y＝kx﹣2与y轴交于点D．
（1）当k＝3时，求A，B两点的坐标；
（2）当△ACD与△BCD的面积比为3：2时，k的值为多少；
（3）将抛物线位于直线AB上方部分沿AB翻折，顶点C的对应点为E，△DEC的面积是否有最大值？若有，求出最大值；若没有，请说明理由．
26．（12分）如图，四边形ABCD为正方形，以A为中心，将线段AB顺时针旋转α°（0°＜α＜90°）得到线段AE，连接DE，BE．
（1）求∠DEB的度数．
（2）过点B作BF⊥DE于点F，连接CF，猜想线段DE与线段CF的数量关系，并证明．
（3）设正方形的边长为m，点G是DE的中点，当CG⊥AE时，求BE的长．（用含m的代数式表示）
参考答案与试题解析
一、选择题（共8小题，每题4分）
1．（4分）的倒数是（ ）
A．B．﹣5C．D．5
【解答】解：∵（﹣）×（﹣5）＝1，
∴﹣的倒数是﹣5，
故选：B．
2．（4分）疫情管控放开，旅游业触底反弹，文旅消费需求剧增．据四川省文化和旅游厅消息，2023年春主假日期间，四川省共接待游客5387.59万人次，居全国第一，实现旅游收入242.16亿元．其中数据5387.59万用科学记数法可表示为（ ）
A．5.38759×103B．5.38759×104
C．5.38759×106D．5.38759×107
【解答】解：5387.59万＝53875900＝5.38759×107．
故选：D．
3．（4分）若x≠y，下列分式化简正确的是（ ）
A．B．C．D．
【解答】解：A、≠，故本选项化简不正确，不符合题意；
B、≠，故本选项化简不正确，不符合题意；
C、≠，故本选项化简不正确，不符合题意；
D、＝＝，本选项化简正确，符合题意；
故选：D．
4．（4分）如图，在△ABC和△DCB中，∠ABC＝∠DCB，只添加一个条件能判定△ABC≌△DCB的是（ ）
A．BC＝CBB．AC＝BDC．AB＝CDD．∠ABC＝∠D
【解答】解：A、BC＝CB是图形中的隐含条件，判定△ABC≌△DCB还缺少一个条件，故A不符合题意；
B、AC＝BD，∠ABC和∠DCB分别是AC和DB的对角，不能判定△ABC≌△∠DCB，故B不符合题意；
C、由SAS判定△ABC≌△DCB，故C符合题意；
D、∠D和∠A是对应角，应该∠A＝∠D，由AAS判定△ABC≌△DCB，故D不符合题意．
故选：C．
5．（4分）某班为了解学生对党史的学习情况，随机抽取了8名学生进行调查，他们读书的本数分别是3、2、3、3、5、1、2、5，则这组数据的中位数是（ ）
A．2B．3C．4D．5
【解答】解：把这组数据从小到大排列为1、2、2、3、3、3、5、5，
排在中间的两个数分别为3，3，故中位数为＝3
故选：B．
6．（4分）如图，正六边形ABCDEF内接于⊙O，点M在上，则∠CME的度数为（ ）
A．36°B．45°C．60°D．75°
【解答】解：如图：连接OC，OD，OE，
∵多边形ABCDEF是正六边形，
∴，
∴∠COE＝2∠COD＝120°，
∴．
故选：C．
7．（4分）我国民间流传着这样一道题：只闻隔壁人分银，不知多少银和人；每人6两多6两，每人半斤少半斤．试问各位善算者，多少人分多少银？（注：在古代，1斤＝16两）设有x人，分银y两，则根据题意可列方程组为（ ）
A．B．
C．D．
【解答】解：设有x人，分银y两，则可列方程组：
．
故选：D．
8．（4分）如图，二次函数y＝ax2+bx+c的图象的对称轴是直线x＝1，下列说法正确的是（ ）
A．ac＜0
B．当x＞﹣1时，y随x的增大而增大
C．b2﹣4ac＜0
D．一元二次方程ax2+bx+c＝0的近似解为x1≈﹣0.5，x2≈3.2
【解答】解：由图象可得，
a＞0，b＜0，c＜0，
∴ac＜0，故选项A正确，符合题意；
当1＞x＞﹣1时，y随x的增大而减小，故选项B错误，不符合题意；
b2﹣4ac＞0，故选项C错误，不符合题意；
一元二次方程ax2+bx+c＝0的近似解为x1≈﹣0.5，x2≈3.5，故选项D错误，不符合题意；
故选：A．
二、填空题（共5小题，每题4分）
9．（4分）计算：（﹣a2）5＝ ﹣a10 ．
【解答】解：（﹣a2）5
＝（﹣1）5a2×5
＝﹣a10．
故答案为：﹣a10．
10．（4分）若反比例函数在每一象限内，y随x的增大而增大，则m的取值范围是 m＜ ．
【解答】解：由题意得的图象在每个象限内y随x的增大而增大，
则2m﹣1＜0，
即m＜．
故答案为：m＜．
11．（4分）如图所示的网格是正方形网格，A，B，C，D，E是网格线的交点，那么△ADE的面积与△ABC的面积的比是 1：4 ．
【解答】解：设正方形网格中的每个小正方形的边长都是1，则AD＝1，AB＝2，
根据勾股定理得AE＝＝2，AC＝＝4，
∴＝＝，
∵∠DAE＝∠BAC，
∴△ADE∽△ABC，
∴＝＝＝，
∴△ADE的面积与△ABC的面积的比是1：4，
故答案为：1：4．
12．（4分）分式方程＝﹣2的解是 x＝1 ．
【解答】解：去分母得：2+x＝﹣1﹣2x+6，
解得：x＝1，
经检验x＝1是分式方程的解，
故答案为：x＝1
13．（4分）如图，在Rt△ABC中，∠C＝90°，按以下步骤作图：①以B为圆心，以任意长为半径作弧，分别交AB，BC于点M，N；②分别以M、N为圆心，以大于MN的长为半径作弧，两弧在∠ABC内交于点P；③作射线BP，交AC于点D．若AB＝5，BC＝3，则线段AD的长为 ．
【解答】解：由作法得BD平分∠ABC，
过D点作DE⊥AB于E，如图，则DE＝DC，
在Rt△ABC中，AC＝＝＝4，
∵S△ABD+S△BCD＝S△ABC，
∴•DE×5+•CD×3＝×3×4，
即5CD+3CD＝12，
∴CD＝，
∴AD＝AC﹣CD＝4﹣＝，
故答案为：．
三、解答题
14．（6分）（1）计算：．
（2）解不等式组：．
【解答】解：（1）
＝2﹣1﹣2×+2﹣
＝2﹣1﹣+2﹣
＝（2﹣1﹣1）+（﹣1+2）
＝1；
（2），
2x+5＞3（x﹣1），
解得：x＜8，
≥﹣1，
解得：x≥﹣，
∴﹣≤x＜8．
15．（8分）第31届世界大学生运动会将于2023年7月28日在成都举行，学校为了了解学生对“大运会”的熟悉程度，在全校范围内随机抽查了部分学生进行调查统计，并将调查统计的结果分为A，B，C三类，A表示“非常熟悉”，B表示“比较熟悉”，C表示“不熟悉”，得到如下统计图（B类有70人），请根据图中提供的信息，解答下列问题：
（1）本次随机调查的人数是 150 人；扇形图中C类所对应的圆心角的度数为 120 度；
（2）若该校共有1500人，请你估计该校B类学生的人数．
（3）若参与调查的两名男生和两名女生中随机抽取2名学生进行“大运会”相关知识问答，请利用画树状图或列表的方法，求恰好抽到一名男生和一名女生的概率．
【解答】解：（1）30÷20%＝150（人），
所以本次随机调查的人数是150人；
C类的人数为150﹣30﹣70＝50（人），
所以扇形图中C类所对应的圆心角的度数为360°×＝120°；
故答案为：150，120°；
（2）1500×＝700（人），
估计该校B类学生的人数为700人；
（3）画树状图为：
共用12种等可能的结果，其中一名男生和一名女生的结果数为8种，
所以恰好抽到一名男生和一名女生的概率＝＝．
16．（8分）三角形具有稳定性，很多展架利用该原理进行设计．如图为一个展架的侧面，展架底部与支架间的距离BD为62cm，展架与地面的夹角为72°，若支架顶部C刚好支在展架的三分之一处（即AB＝3AC），且CD＝BC，那么该展架AB的长为多少．（结果精确到1cm；参考数据：sin72°≈0.95，cs72°≈0.31，tan72°≈3.08）
【解答】解：作CE⊥BD于点E．
∴∠CEB＝90°．
∵BC＝CD，BD＝62cm．
∴BE＝BD＝31cm．
∵∠B＝72°，csB＝．
∴≈0.31，
解得：BC＝100（cm）．
∵AB＝3AC，
∴BC＝AB．
∴AB＝BC＝150（cm）．
答：该展架AB的长为约为150cm．
17．（10分）如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，以CD为直径作⊙O，交BC边于点E，过点E作EF⊥AB，垂足为点F．
（1）求证：EF为⊙O的切线；
（2）若AC＝6，CD＝5，求DF的长．
【解答】（1）证明：如图，连接OE，DE，
∵CD是⊙O直径，
∴∠CED＝90°，
即DE⊥BC，
∵在Rt△ABC中，∠ACB＝90°，D为AB的中点，
∴CD＝BD，
∴点E是BC的中点，
又∵点O是CD的中点，
∴OE是△BCD的中位线，
∴OE∥AB，
∵EF⊥AB，
∴EF⊥OE，
∵OE是⊙O的半径，
∴EF是⊙O的切线；
（2）解：∵CD是直角三角形ABC斜边中线，CD＝5，
∴AB＝2CD＝10，
∵AC＝6，
∴BC＝＝8，
∵点E是BC的中点，
∴BE＝BC＝4，
在Rt△BDE中，BD＝5，BE＝4，
∴DE＝＝3，
∵S△BDE＝DE•BE＝BD•EF，即3×4＝5×EF，
∴EF＝，
在Rt△DEF中，DE＝3，EF＝，
∴DF＝＝．
18．（10分）已知一次函数y1＝x+2与反比例函数y2＝的图象交于A、B两点，交y轴于点C．
（1）当A点的横坐标为4时，求反比例函数的表达式和点B的坐标；
（2）在（1）的条件下，若点A关于原点的对称点为A'，求△AA′B的面积；
（3）探究：点P在y轴上，是否存在一点P，使得△ABP为等腰直角三角形，且直角顶点为点P．若存在，求出P点坐标及此时的k值；若不存在，请说明理由．
【解答】解：（1）设点A（4，m），
∵一次函数y1＝x+2图象过点A，
∴m＝×4+2＝4，
∴A（4，4），
∵反比例函数y2＝的图象过点A（4，4），′
∴k＝4×4＝16，
∴反比例函数的表达式为y2＝，
由，
解得或，
∴B点的坐标为（﹣8，﹣2）；
（2）如图：
∵A（4，4），
∴点A关于原点的对称点为A'的坐标为（﹣4，﹣4），
∵B（﹣8，﹣2），
∴△AA′B的面积＝（4+8+8﹣4）×（4+4）﹣×（8+4）××4×2＝24；
（3）如图，过点A作AE⊥y轴于E，BD⊥y轴于D，
∴∠AEP＝∠BDP＝90°，
设点A（a，a+2），（a＞0），
∴AE＝a，k＝a（a+2），
联立方程可得：x+2＝，
∴x1＝a，x2＝﹣a﹣4，
∴点B（﹣a﹣4，﹣a），
∴BD＝a+4，DO＝a，
∵△ABP为等腰直角三角形，
∴BP＝AP，∠APB＝90°＝∠AEP＝∠BDP，
∴∠APE+∠BPD＝90°＝∠APE+∠PAE，
∴∠BPD＝∠PAE，
∴△BPD≌△PAE（AAS），
∴BD＝PE＝a+4，AE＝PD＝a，
∵OE＝a，
∴PO＝4，
∴点P（0，﹣4），
∵OP＝OD+PD，
∴4＝a+a，
∴a＝，
∴k＝（×+2）＝．
一、填空题（共5小题，每小题4分）
19．（4分）已知x2+3x+1＝0，则代数式的值为 1 ．
【解答】解：÷
＝•
＝（x+1）（x+2）
＝x2+3x+2，
∵x2+3x+1＝0，
∴x2+3x＝﹣1，
∴原式＝﹣1+2＝1，
故答案为：1．
20．（4分）如图，平面直角坐标系中一条圆弧经过网格点A，B，C，点A在y轴上，点B的坐标为（4，4），则该圆弧AC的长为 π ．
【解答】解：如图，借助网格作AB的中垂线MN，BC的中垂线PQ，直线PQ，MN相交于点D，即弧AC所在的圆心为D，
连接AD、CD，
∵OD＝EC＝2，OA＝DE＝4，∠AOD＝∠DEC，
∴△AOD≌△DEC（SAS），
∴∠ADO＝∠ECD，
∵∠ECD+∠CDE＝90°，
∴∠ADO+∠CDE＝90°，
又∵∠ADO+∠CDE+∠ADC＝180°，
∴∠ADC＝180°﹣90°＝90°，
在Rt△AOD中，OA＝4，OD＝2，
∴AD＝＝2，
∴弧AC的长为＝π．
故答案为：π．
21．（4分）有五张正面分别写有数字﹣4，﹣3，0，2，3的卡片，五张卡片除了数字不同外其余全部相同，现将它们背面朝上，洗匀后从中随机抽取一张，记卡片上的数字为n，则抽取的n既能使关于x的方程x2﹣2（n+1）x+n（n﹣3）＝0有实数根，又能使以x为自变量的二次函数y＝﹣x2+2nx+1，当x＞2时，y随x增大而减小的概率为 ．
【解答】解：∵关于x的方程x2﹣2（n+1）x+n（n﹣3）＝0有实数根，
∴Δ＝[﹣2（n+1）]2﹣4n（n﹣3）＝20n+4≥0，
解得n≥﹣，
∵二次函数y＝﹣x2+2nx+1，当x＞2时，y随x增大而减小，
∴n≤2，
∴满足条件的n有0，2，
∴当x＞2时，y随x增大而减小的概率为2÷5＝．
故答案为：．
22．（4分）在平面直角坐标系中，以P（t，0）为圆心，单位长1为半径的圆与直线y＝kx﹣3相切于点M，直线y＝kx﹣3与x轴交于点A，与y轴交于点N，当MN取得最小值时，点A的坐标为 或 ．
【解答】解：对于y＝kx﹣3，当x＝0时，y＝﹣3，
∴直线y＝kx﹣3与y轴交于点N的坐标为（0，﹣3），
∵点P（t，0），
∴，
∵MN为⊙P的切线，M为且点，⊙P的半径为1，
∴PM⊥MN，PM＝1，
在Rt△PMN中，，PM＝1，
由勾股定理得：MN＝＝，
∵，
∴当t＝0时，为最小，最小值为，
此时点P的坐标为（0，0），如图所示：

设直线y＝kx﹣3与x轴交于点A的坐标为（a，0），
则PA＝|a|，，
由三角形的面积公式得：S△PAN＝PA•PN＝AN•PM，
即PA•PN＝AN•PM，
∴，
解得：，
∴点A的坐标为或．
故答案为：或．
23．（4分）如图，在平面直角坐标系xOy中，点A的坐标为，点C在函数的图象上，若点A绕点C顺时针旋转120°，所得对应点B刚好落在y轴的正半轴上，则线段AB的长为 ．
【解答】解：如图，
过点C作CD⊥x轴于点D，作CE⊥y轴于点E，将△CBE绕C点顺时针旋转120°，得△CAF，延长CF交x轴于点H，则∠DCF＝30°，
设，
则：CF＝CE＝c，，
∴，，
∴，
∵点，
∴，
∵∠AHF＝90°﹣∠DCH＝60°，
∴AH＝2FH，
∴，
∴，
∴OE＝CD＝5，，
∴，
∴BC2＝AC2＝CD2+AD2＝28，
∴，
∴OB＝OE+BE＝5+1＝6，
∴．
二、解答题
24．（8分）晚饭后，小萌和妈妈出门散步，两人同时从家门口出发，小萌骑上新学会的平衡车，骑行3分钟后，他发现妈妈没有跟上，于是立刻掉头，以1.5倍的速度回去接妈妈．妈妈步行的速度是60m/min，小萌与妈妈的距离y（m）与骑行的时间x（min）之间的关系如图所示．
（1）求出AB所在直线的函数关系式；
（2）小萌掉头后多久接到妈妈？
【解答】解：（1）由题意得，点M的坐标为（3，480），
小萌开始骑行的速度为：480÷3+60＝220（m/min），
∴小萌后来的速度为：220×1.5＝330（m/min），
∴点A的横坐标为：3+480÷（330+60）＝3+＝，
设AB所在直线的函数关系式为y＝kx+b，
则，
解得，
∴AB所在直线的函数关系式为y＝﹣390x+1650；
（2）480÷（330+60）＝（min），
即小萌掉头后min接到妈妈．
25．（10分）如图，在平面直角坐标系xOy中，直线y＝kx﹣2与抛物线y＝﹣x2+2相交于A，B两点（点A在点B的左侧）．若抛物线y＝﹣x2+2的顶点为C，直线y＝kx﹣2与y轴交于点D．
（1）当k＝3时，求A，B两点的坐标；
（2）当△ACD与△BCD的面积比为3：2时，k的值为多少；
（3）将抛物线位于直线AB上方部分沿AB翻折，顶点C的对应点为E，△DEC的面积是否有最大值？若有，求出最大值；若没有，请说明理由．
【解答】解：（1）当k＝3时，y＝3x﹣2，
联立，
解得或，
∴A（﹣4，﹣14），B（1，1）；
（2）过A作AK⊥y轴于K，过B作BT⊥y轴于T，如图：
联立可得x2+kx﹣4＝0，
∴xA＝，xB＝，
∵△ACD与△BCD的面积比为3：2，
∴＝，
∴＝，即＝，
∴＝，
解得k＝或k＝﹣（舍去），
∴k的值为；
（3）△DEC的面积有最大值，理由如下：
过E作EH⊥y轴于H，如图：
抛物线y＝﹣x2+2的顶点C坐标为（0，2），
在y＝kx﹣2中令x＝0得y＝﹣2，
∴D（0，﹣2），
∴CD＝2﹣（﹣2）＝4，
∴S△DEC＝CD•EH＝2EH，
∴当EH最大时，△DEC的面积最大，
∵将抛物线位于直线AB上方部分沿AB翻折，顶点C的对应点为E，
∴C，E关于直线AB对称，
∴DE＝CD＝4，
由垂线段最短可得，HE≤4，即HE的最大值为4，
∴△DEC的面积最大为2EH＝2×4＝8．
26．（12分）如图，四边形ABCD为正方形，以A为中心，将线段AB顺时针旋转α°（0°＜α＜90°）得到线段AE，连接DE，BE．
（1）求∠DEB的度数．
（2）过点B作BF⊥DE于点F，连接CF，猜想线段DE与线段CF的数量关系，并证明．
（3）设正方形的边长为m，点G是DE的中点，当CG⊥AE时，求BE的长．（用含m的代数式表示）
【解答】解：（1）∵四边形ABCD是正方形，
∴AB＝AD，∠BAD＝90°，
由旋转得：AE＝AB，∠BAE＝α，
∴∠DAE＝90°+α，
∴∠AEB＝，∠AED＝＝，
∴∠DEB＝∠AEB﹣∠AED＝﹣＝45°．
（2）猜想：DE＝CF，理由如下：
如图，过C作CH⊥CF交FD延长线于H，
∵BF⊥DE，
∴∠BFC+∠CFD＝90°，
∵CH⊥CF，
∴∠CFD+∠H＝90°，
∴∠BFC＝∠H，
∵∠BCD＝∠FCH＝90°，
∴∠BCF＝∠DCH，
∵BC＝CD，
∴△BCF≌△DCH（AAS），
∴BF＝DH，CF＝CH，
∴△FCH是等腰直角三角形，
∴FH＝CF，
由（1）知，∠DEB＝45°，
∴△BEF是等腰直角三角形，
∴BF＝EF，
∴EF＝DH，
∴EF+DF＝DH+DF，
即DE＝FH，
∴DE＝CF．
（3）如图，延长CG交AE于H，过点B作BL⊥AG于L，BT⊥DE于T，过点C作CK⊥DE于K，设DE交AB于S，
则∠EHG＝∠CKD＝90°，
∵四边形ABCD是正方形，
∴AD＝CD，∠ADC＝90°，
∵AE＝AD，点G是DE的中点，
∴∠AGE＝∠AGD＝90°，
∴∠CKD＝∠AGD，
∵∠ADG+∠DAG＝∠ADG+∠CDK＝90°，
∴∠DAG＝∠CDK，
在△ADG和△DCK中，
，
∴△ADG≌△DCK（AAS），
∴AG＝DK，DG＝CK，
由（1）知∠AED＝∠ADE＝，
∴∠CGD＝∠EGH＝90°﹣＝，
∵∠CDG＝∠ADC﹣∠ADE＝90°﹣＝，
∴∠CGD＝∠CDG，
∴CG＝CD＝m，
∵CK⊥DG，
∴DK＝GK＝DG，
∵∠AGD＝∠DAS，∠ADG＝∠SDA，
∴△ADS∽△GDA，
∴＝＝，
∴＝，
∴AS＝BS，
在△ASG和△BST中，
，
∴△ASG≌△BST（AAS），
∴BT＝AG，
由（2）知△BET是等腰直角三角形，
∴BE＝BT＝AG，
在Rt△ADG中，AG2+DG2＝AD2，
即AG2+（2AG）2＝m2，
∴AG＝m，
∴BE＝AG＝×m＝m．