2023-2024学年江苏省南京市玄武区七年级（上）期中数学试卷（含解析）

这是一份2023-2024学年江苏省南京市玄武区七年级（上）期中数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.−2023的相反数是
( )
A. 12023B. −12023C. 2023D. −2023
2.第19届亚运会在杭州举办，组委会招募志愿者约152万．将152万用科学记数法表示为( )
A. 152×104B. 15.2×105C. 1.52×106D. 0.152×107
3.在−47,1.010010001,0,π2,0.1222⋅⋅⋅,20%,−2.626626662⋅⋅⋅(每两个2之间依次多一个6)中，无理数共有
( )
A. 1个B. 2个C. 3个D. 4个
4.在跳远测试中，小明的成绩为2.1米，记作+0.5米．若小亮的成绩记作−0.2米，则小亮的成绩为
( )
A. 1.4米B. 1.6米C. 1.8米D. 1.9米
5.下列等式正确的是( )
A. −2x+1=−2x+1B. −−2x−1=−2x+1
C. −3x−2=−3x+2D. −−2x−3=2x−3
6.某工厂计划生产n个零件，原计划每天生产a个零件，实际每天比原计划多生产b个零件，则实际生产所用的天数比原计划少
( )
A. na−nb天B. nb−na天C. na+b−na天D. na−na+b天
7.如图，数轴上，点A、B表示的数分别是a、b，下列结论：①−a>−b；②1a<1b；③a2>b2；④a3( )
A. 1个B. 2个C. 3个D. 4个
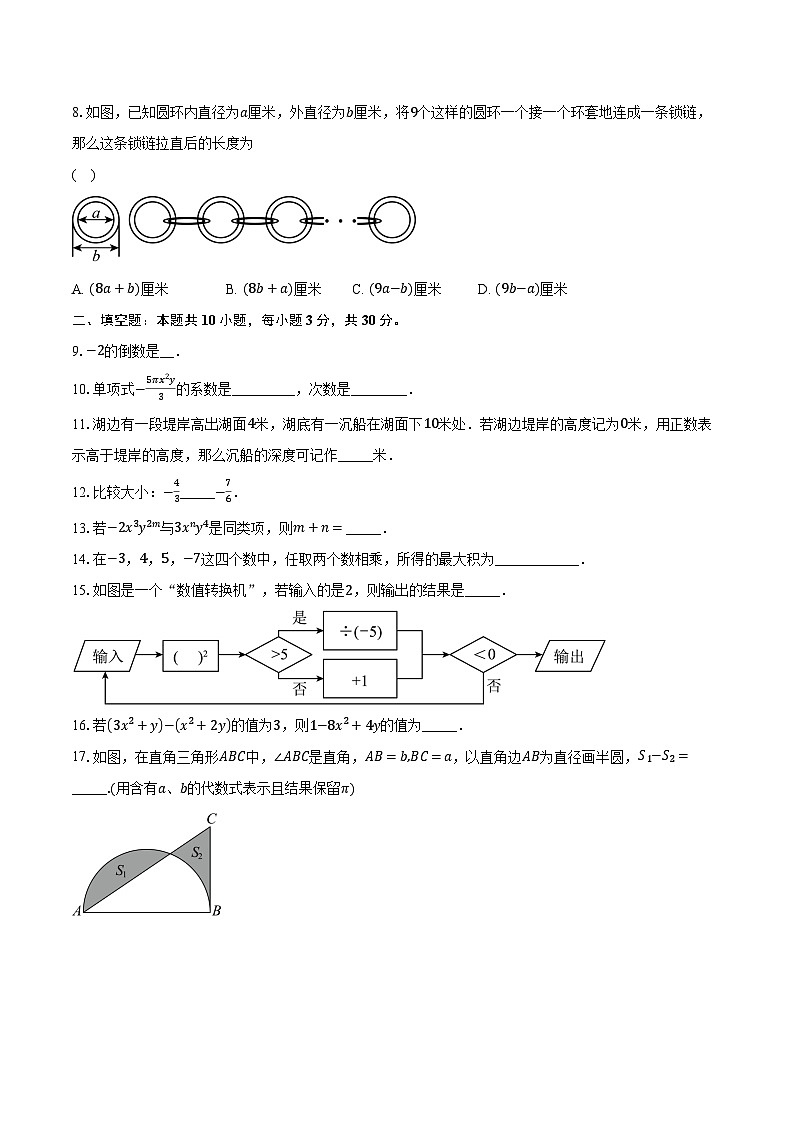
8.如图，已知圆环内直径为a厘米，外直径为b厘米，将9个这样的圆环一个接一个环套地连成一条锁链，那么这条锁链拉直后的长度为
( )
A. 8a+b厘米B. 8b+a厘米C. 9a−b厘米D. 9b−a厘米
二、填空题：本题共10小题，每小题3分，共30分。
9.−2的倒数是__．
10.单项式−5πx2y3的系数是_________，次数是________．
11.湖边有一段堤岸高出湖面4米，湖底有一沉船在湖面下10米处．若湖边堤岸的高度记为0米，用正数表示高于堤岸的高度，那么沉船的深度可记作_____米．
12.比较大小：−43_____−76．
13.若−2x3y2m与3xny4是同类项，则m+n=_____．
14.在−3，4，5，−7这四个数中，任取两个数相乘，所得的最大积为____________．
15.如图是一个“数值转换机”，若输入的是2，则输出的结果是_____．
16.若3x2+y−x2+2y的值为3，则1−8x2+4y的值为_____．
17.如图，在直角三角形ABC中，∠ABC是直角，AB=b,BC=a，以直角边AB为直径画半圆，S1−S2=_____.(用含有a、b的代数式表示且结果保留π)
18.将9个代数式填入九宫格的方格中，使得九宫格的每一横行、每一竖列以及两条对角线上的3个代数式的和都相等．已知九宫格中的部分代数式如图所示，则M−N=_____.(用含有x的代数式表示)
三、计算题：本大题共2小题，共12分。
19.计算
(1)20−17−(−7)+(−16)；
(2)5÷23×32÷(−5)；
(3)−25−2+110÷−110；
(4)−22−113÷1−43×(1−2)2023．
20.化简
(1)−x−2y2+3x+4y2；
(2)3ab−a2+2a2−2ab．
四、解答题：本题共7小题，共56分。解答应写出文字说明，证明过程或演算步骤。
21.(本小题8分)
先化简，再求值：x2+2xy−3y2−2x2+2xy−2y2，其中x=−1，y=−2．
22.(本小题8分)
甲、乙两家水果店某一周的销售金额以每天1000元为准，超过的金额记作正数，不足的金额记作负数，记录情况如下表所示．其中乙水果店周三的销售金额被墨水涂污．
(1)求甲水果店该周的销售总金额；
(2)若甲、乙两家水果店该周的销售总金额相等，求乙水果店周三的销售金额．
23.(本小题8分)
定义新运算“⊙”：对于有理数a，b(b≠0)，都有a⊙b=−a+1b.例如：2⊙3=−2+13=−53．
(1)计算：2⊙12= ，2023⊙12023⊙12023= ；
(2)化简：a⊙b⊙b⋅⋅⋅b⊙b2n+1个b= (n是正整数)．
24.(本小题8分)
如图，某体育公园有一块长为90米，宽为70米的长方形运动场地．场地中间有两块运动区域，分别记作①号和②号区域．阴影部分为人行通道，两条横向通道和三条纵向通道的宽度均相等．已知①号区域的形状是正方形，边长为a米，②号区域的形状是长方形．
(1)当a=60时，人行通道的宽度为 米；
(2)求②号区域的周长(用含a的代数式表示)．
25.(本小题8分)
数轴上，点A、B表示的数分别是a、b，请用刻度尺或圆规完成下列画图．(保留画图痕迹，写出必要的文字说明)
(1)如图①，在数轴上画出点P，且点P表示的数是a+b；
(2)如图②，点C表示的数是a+b，在数轴上画出原点O．
26.(本小题8分)
某网约车的车费由里程费、时长费、远途费三部分构成车费计价规则如下表：
(1)若行车里程为30千米，时长为40分钟，需付车费 元；
(2)若行车里程为m千米，时长为n分钟，求应付的车费；(用含m、n的代数式表示)
(3)乘坐该网约车去某地，导航显示两条路线．
路线1：行车里程为x(510)分钟；
路线2：行车里程比路线1多5千米，时长比路线1少10分钟．
请问选择哪一条路线所付车费较少？并说明理由．
27.(本小题8分)
“距离”再探究．
【概念理解】
(1)数轴上，点A、B表示的数分别是−1、2，则A、B两点之间的距离可以表示为 ．
A.2−1 B．2+−1 C．2−1 D．2−−1
【数学思考】
(2)数轴上，点C、D、E表示的数分别是2、4、10．P是数轴上的动点，设点P表示的数是x．
(Ⅰ)点P到C、D两点的距离之和的最小值为 ；
(Ⅱ)填写表格，并回答问题：
当x= 时，x−2+x−4+x−10取最小值．
【实际应用】
(3)如图，在一条笔直的道路l上分别有A、B、C、D四个停车场．为满足充电需要，在道路l上修建一个充电站P.已知A、B、C、D四个停车场分别有2m+9辆，m+1辆，m+3辆，6辆电动车需要充电，其中m为正整数．请问充电站P建在道路l上何处时，四个停车场中的所有电动车到充电站P的距离之和最小？并简要说明理由．(在停车场内移动的距离忽略不计)．
答案和解析
1.【答案】C
【解析】略
2.【答案】C
【解析】【分析】本题主要考查科学记数法，根据科学记数法的表示方法求解即可．科学记数法的表示形式为a×10n的形式，其中1≤a<10，n为整数．解题关键是正确确定a的值以及n的值．
【详解】将152万用科学记数法表示为1.52×106．
故选：C．
3.【答案】B
【解析】【分析】本题考查了无理数的识别，无限不循环小数叫无理数，初中范围内常见的无理数有：①含π类，如2π，π3等；②开方开不尽的数，如 2，35等；③具有特殊结构的数，如0.1010010001…(两个1之间依次增加1个0)，0.2121121112…(两个2之间依次增加1个1)．
【详解】解：−47,1.010010001,0,0.1222⋅⋅⋅,20%是有理数，
π2,−2.626626662⋅⋅⋅(每两个2之间依次多一个6)是无理数．
故选B．
4.【答案】A
【解析】【分析】本题考查正数和负数及有理数运算的实际应用，结合已知条件列得正确的算式是解题的关键．根据正数和负数的实际意义列式计算即可．
【详解】解：由题意可得标准为2.1−0.5=1.6(米)，
∵小亮的成绩记作−0.2米，
∴小亮的成绩为1.6−0.2=1.4(米)，
故选：A．
5.【答案】C
【解析】【分析】题考查了去括号，熟练掌握去括号法则是关键．当括号前是“+”号时，去掉括号和前面的“+”号，括号内各项的符号都不变号；当括号前是“−”号时，去掉括号和前面的“−”号，括号内各项的符号都要变号．
【详解】解：A．−2x+1=−2x−1，故不正确；
B.−−2x−1=2x+1，故不正确；
C.−3x−2=−3x+2，正确；
D.−−2x−3=2x+3，故不正确；
故选C．
6.【答案】D
【解析】【分析】本题主要考查根据实际问题列代数式，表示出原计划生产所用的天数和实际生产所用的天数，然后相减即可．根据题意表示出原来和现在所用的天数是关键．
【详解】根据题意得，
原计划生产所用的天数为na，
实际生产所用的天数为na+b，
∴实际生产所用的天数比原计划少na−na+b天．
故选：D．
7.【答案】D
【解析】【分析】本题考查了有理数在数轴上的表示，有理数的乘方法则的理解等知识，根据数轴确定a，b的符号，根据有理数的乘方法则判断即可．熟练掌握有理数的基本知识是解题的关键．
【详解】∵数轴上，点A、B表示的数分别是a、b，
∴a<0b，
∴①−a>−b，故①正确；
∴②1a<1b，故②正确；
∴③a2>b2，故③正确；
∴④a3综上所述，正确的个数有4个．
故选：D．
8.【答案】A
【解析】本题考查了图形类规律探究，正确归纳类推出一般规律是解题关键．先分别求出将2、3、4个这样的圆环一个接一个环套地连成条锁链拉直后的长度，再归纳类推出一般规律，由此即可得．
【详解】
解：根据题意可知，1个圆环的最长长度是(b−a+a=b厘米；
2个圆环套成的链条拉直后的长度是b−a+2a=b+a厘米；
3个圆环套成的链条拉直后的长度是b−a+3a=b+2a厘米；
4个圆环套成的链条拉直后的长度是b−a+4a=b+3a厘米；
…；
9个圆环套成的链条拉直后的长度是b−a+9a=b+8a厘米．
故选：A．
9.【答案】−12
【解析】【分析】直接利用倒数的定义得出答案．
【详解】根据两个数乘积是1的数互为倒数的定义，因此求一个数的倒数即用1除以这个数．
所以−2的倒数为1÷−2=−12．
故答案为：−12．
此题主要考查了倒数的定义，正确掌握相关定义是解题关键
10.【答案】 −5π3 3
【解析】【分析】直接利用单项式的次数与系数的概念分析得出即可．
【详解】单项式−5πx2y3的系数是：−5π3，次数是：3．
故答案为：−5π3，3．
【点睛】本题考查了单项式的系数和次数的定义，单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数．在判别单项式的系数时，要注意包括数字前面的符号，还要注意π不是字母．
11.【答案】−14
【解析】【分析】本题考查正数和负数，理解具有相反意义的量是解题的关键．正数和负数是一组具有相反意义的量，据此即可求得答案．
【详解】解：由题意可得沉船的深度可记作−14米，
故答案为：−14．
12.【答案】<
【解析】【分析】此题主要考查了有理数大小比较，直接利用负数比较大小的方法分析得出答案，两个负数，比较它们的绝对值大小，绝对值大的反而小．正确掌握比较方法是解题关键．
【详解】解：∵−43=43=86，−76=76，86>76，
∴−43<−76．
故答案为：<．
13.【答案】5
【解析】【分析】本题考查了利用同类项的定义求字母的值，熟练掌握同类项的定义是解答本题的关键．先根据同类项的定义求出m和n的值，再把求得的m和n的值代入所给代数式计算即可．
【详解】解：−2x3y2m与3xny4是同类项，
∴n=3,2m=4，
∴m=2，
∴m+n=3+2=5．
故答案为：5．
14.【答案】21
【解析】【分析】两个数相乘，同号得正，异号得负，且正数大于一切负数，所以找积最大的应从同号的两个数中寻找即可．
【详解】解：4×5=20，(−3)×(−7)=21，
∵21>20，
∴所得的积最大为21．
故答案为21．
【点睛】本题考查有理数的乘法及有理数大小比较，关键要明确不为零的有理数相乘的法则：两数相乘，同号得正，异号得负，并把绝对值相乘．
15.【答案】−5
【解析】【分析】本题考查了有理数的混合运算，利用程序图的程序列式计算即可．
【详解】解：若输入的是2，则22+1=4+1=5，不小于0，
∴重新输入的是5，则52÷−5=25÷−5=−5<0，
∴输出的结果是−5．
故答案为：−5．
16.【答案】−11
【解析】【分析】本题考查了整式的加减，整体代入法求代数式的值．先根据3x2+y−x2+2y的值为3求出2x2−y=3，再代入1−8x2+4y计算即可．
【详解】解：∵3x2+y−x2+2y的值为3，
∴3x2+y−x2+2y=3，
∴3x2+y−x2−2y=3，
∴2x2−y=3，
∴1−8x2+4y
=1−42x2−y
=1−4×3=−11．
故答案为：−11．
17.【答案】πa28−ab2
【解析】【分析】本题考查整式的加减，理解题意，理清数量关系是解决问题的关键．分别表示出S1,S2的面积，然后相减即可．
【详解】解：根据已知半圆面积为=12πb22=18πb2，
∴S1=18πb2−S′，
∵S▵ABC=12AB⋅BC=12ab，
∴S2=12ab−S′，
∴S1−S2=18πb2−S′−12ab−S′
=18πb2−S′−12ab+S′
=18πb2−12ab．
故答案为：18πb2−12ab．

18.【答案】−2x2+4x/4x−2x2
【解析】【分析】此题考查了整式的加减混合运算，设最中间的代数式为P，然后根据题意用含x的代数式表示出P，M，N，进而可求出M−N.解题的关键是读懂题意，用含x的代数式表示出M和N．
【详解】设最中间的代数式为P，
∵九宫格的每一横行、每一竖列以及两条对角线上的3个代数式的和都相等，
∴x2−x+x−1+N=x2−x+P+x2−x−1
∴解得P=−x2+2x+N
∴第一列中间的代数式为x2−x+x−1+N−−x2+2x+N+x=2x2−3x−1
∵第一列的三个数之和等于第三行的三个数之和，
∴M+2x2−3x−1+x2−x=x2−x+x−1+N
化简得，M−N=−2x2+4x．
故答案为：−2x2+4x．
19.【答案】(1)原式=20−17+7−16
=10−16
=−6
(2)原式=5×32×32×−15
=5×−15×32×32
=−94
(3)原式=−25−2+110×−10
=−25×−10−2×−10+110×−10
=4+20−1=23
(4)原式=−4−43÷43×−1
=−4+43×34
=−3

【解析】【分析】本题考查了有理数的混合运算，熟练掌握运算法则是解答本题的关键．
(1)先把减法统一成加法，再按加法法则计算；
(2)先把除法转化为乘法，再按乘法法则计算；
(3)先把除法转化为乘法，再按乘法分配律计算；
(4)先算乘方和绝对值，再算除法和乘法，然后算加减．
20.【答案】(1)原式=−x+3x−2y2+4y2
=2x+2y2．
(2)原式=3ab−3a2+2a2−4ab
=−3a2+2a2+3ab−4ab
=−a2−ab．

【解析】【分析】本题考查了整式的加减，整式加减的运算法则：一般地，几个整式相加减，如果有括号先去括号，然后再合并同类项．
(1)直接合并同类项即可；
(2)先去括号，再合并同类项即可．
21.【答案】解：x2+2xy−3y2−2x2+2xy−2y2
=x2+2xy−3y2−2x2−4xy+4y2
=x2−2x2+2xy−4xy−3y2+4y2
=−x2−2xy+y2
当x=−1，y=−2时，
原式=−(−1)2−2×−1×−2+(−2)2
=−1−4+4
=−1．

【解析】【分析】此题考查了整式的加减混合运算，先去括号，再合并同类项，然后将已知数据代入计算即可得出答案．熟练掌握去括号、合并同类项法则是解本题的关键．
22.【答案】(1)甲水果店的销售总额为：1000×7+0+82+60−32−60+521+479=8050(元)，
所以甲水果店的销售总额为8050元；
(2)设乙水果店周三的销售金额为x元，
1000×7+30+50+x−20+99+551+400=8050，
x=−60，
∴乙水果店周三的销售金额1000−60=940(元)．

【解析】【分析】本题考查了有理数的混合运算，一元一次方程的应用，正确秀出方程是解题关键．
(1)根据题意列出算式计算即可；
(2)根据题意列出一元一次方程，计算即可．
23.【答案】(1)2⊙12=−2+2=0，
2023⊙12023⊙12023
=−2023+2023⊙12023
=0⊙12023
=0+2023
=2023；
(2)原式=−a+1b⊙b⊙b⊙b...⊙b
=a−1b+1b⊙b⊙b...⊙b
=a⊙b⊙b...⊙b
…
=−a+1b．
故答案为：−a+1b．

【解析】【分析】本题考查新运算及有理数的运算，结合已知条件列得正确的算式是解题的关键．
(1)根据定义的新运算列式计算即可；
(2)根据定义的新运算列式计算即可．
24.【答案】(1)当a=60时，
人行通道的宽度为：70−60÷2=5(米)，
故答案为：5；
(2)因为①号区域是正方形且通道宽度都相等，矩形运动场宽70米，
所以通道的宽度可以表示为1270−a米：
因为矩形运动场的长为90米，
所以②号区域宽为90−3×1270−a−a=12a−15
因为②号区域长为a米，宽为12a−15米，
所以②号区域得周长为2a+12a−15=3a−30，
答：②号区域得周长为3a−30米．

【解析】【分析】本题主要考查了列代数式，求代数式的值，正方形与长方形的性质，熟练掌握长方形与正方形的性质是解题的关键．
(1)利用长方形与正方形的性质，利用大长方形的宽减去正方形的边长即得到两条人行通道的宽度；
(2)利用(1)中的方法求得人行通道的宽度，利用图中数据求得②号区域的宽，再利用正方形的周长公式解答即可．
25.【答案】(1)
点P即为所求．
(2)
点O即为所求．

【解析】【分析】本题考查了有理数的加法运算，数轴．
(1)以B为圆心，点A到原点的距离为半径画弧，交数轴于点P，点P即为所求．
(2)以B为圆心，AC长为半径画弧，交数轴于点O，点O即为所求．
26.【答案】(1)里程费：1.6×30=48(元)，
时长费：0.5×40=20(元)，
里程30千米>10千米，远途费：0.4×30−10=8(元)，
共计：48+20+8=76(元)，
故答案为：76；
(2)当0≤m≤10时，应付车费为1.6m+0.5n(元)
当m>10时，应付车费为1.6m+0.5n+0.4m−10=2m+0.5n−4(元)
(3)路线1的费用为1.6x+0.5y(元)；
路线2的费用为1.6x+5+0.5y−10−0.4x+5−10=2x+0.5y+1(元)；
2x+0.5y+1−1.6x+0.5y=0.4x+1，
因为50，
故2x+0.5y+1>1.6x+0.5y，
因此，路线1的费用较少．

【解析】【分析】此题考查了列代数式，分别列出两种线路应付的车费，然后用作差法比较两个代数式的大小是解本题的关键．
(1)根据网约车行车计费规则进行计算即可求解；
(2)根据m的值在10千米以内还是超过10千米，分别写出应付车费即可；
(3)分别用含x、y的代数式表示线路1和线路2应付的车费，再用作差法比较两个代数式的大小即可．
27.【答案】(1)A、B两点之间的距离可以表示为2−−1，
故选：D；
(2)(Ⅰ)点P到C、D两点的距离之和为：x−2+x−4，
当x<2时，x−2+x−4=2−x+4−x=6−2x>2，
当2≤x≤4时，x−2+x−4=2−x+x−4=2，
当x>4时，x−2+x−4=x−2+x−4=2x−6>2，
点P到C、D两点的距离之和的最小值为2，
(Ⅱ)点P到C、D、E三点的距离之和为：x−2+x−4+x−10，
当x=3时，x−2+x−4+x−10=9，
当x=4时，x−2+x−4+x−10=8，
当x<2时，x−2+x−4+x−10=2−x+4−x+10−x=16−3x>10，
当2≤x<4时，x−2+x−4+x−10=x−2+4−x+10−x=12−x，
即有8<12−x≤10，
当4≤x<10时，x−2+x−4+x−10=x−2+x−4+10−x=4+x，
即有8≤4+x<14，且当x=4时，x−2+x−4+x−10=4+x=8，
当x≥10时，x−2+x−4+x−10=x−2+x−4+x−10=3x−16≥14，
即当x=4时，x−2+x−4+x−10取最小值，最小值为8．
故答案为：(Ⅰ)2；(Ⅱ)9，8，4；
(3)充电站P建在B停车场．理由如下：
A、B、C、D四个停车场分别有2m+9辆，m+1辆，m+3辆，6辆电动车需要充电，
∵m为正整数，
∴2m+9≥11>6，2m+9>m+3>m+1，
如图，
先只考虑停车场A与停车场D，将停车场A的车辆数分为6辆和2m+3辆两个部分，
车辆数为6辆的停车场A与停车场D之间建充电站P，
根据(2)(I)的结论可知：当充电站P建在AD之间(含两端端点)时，此时停车场A与停车场D的共计12辆电动车到充电站P的距离之和最小；
现在讨论余下车辆数为2m+3辆的停车场A、停车场B、停车场C之间建充电站P的问题，
如图，
同理：再将余下停车场A的车辆数分为m辆和m+3辆两个部分，
车辆数为m+3辆的停车场A与停车场C之间建充电站P，
根据(2)(I)的结论可知：当充电站P建在AC之间(含两端端点)时，此时停车场A与停车场C的共计2m+3辆电动车到充电站P的距离之和最小；
现在讨论余下车辆数为m辆的停车场A、停车场B之间建充电站P的问题，
如图，
∵m∴再将停车场B的车辆数分为m辆和1辆两个部分，
车辆数为m辆的停车场A与车辆数为m辆的停车场B之间建充电站P，
根据(2)(I)的结论可知：当充电站P建在AB之间(含两端端点)时，此时停车场A与停车场B的共计2m辆电动车到充电站P的距离之和最小；
此时还剩下B停车场的1辆车，
当充电站P建在停车场B时，B停车场剩下的1辆车到充电站的距离为0，即距离最小，
充电站的建设范围由AD缩小至AC，再缩小至AB，最后确定在点B，
综上：充电站P建在B停车场．

【解析】【分析】(1)两数相减，再取绝对值即可作答；
(2)(Ⅰ)先得出点P到C、D两点的距离之和为：x−2+x−4，在分类讨论即可作答；(Ⅱ)点P到C、D、E三点的距离之和为：x−2+x−4+x−10，同理分类讨论即可作答；
(3)除距离外，还涉及到车的数量，总距离等于车的数量乘以单辆车所走的距离．为了运用第(2)的结论，则必须要构造出车辆数相等的点(停车场)，据此逐步缩小范围即可作答．
【点睛】本题考查了数轴，代数式与数轴的应用，问题的难点在第(3)问，构造出车辆数相等的点(停车场)，是解答本题的关键．
日期
周一
周二
周三
周四
周五
周六
周日
甲
0
+82
+60
−32
−60
+521
+479
乙
+30
+50
−20
+99
+551
+400
里程费
时长费
远途费
单价
1.6元/千米
0.5元/分钟
当里程不超过10千米，不收费用；当里程超过10千米，超过10千米的部分以0.4元/千米额外加收费用．
x
…
3
4
5
6
…
点P到C、D、E三点的距离之和
…
①
②
9
10
…