辽宁省抚顺新市抚区2023-2024学年九年级下学期3月教学质量检测数学试题（原卷版+解析版）

这是一份辽宁省抚顺新市抚区2023-2024学年九年级下学期3月教学质量检测数学试题（原卷版+解析版），文件包含辽宁省抚顺新市抚区2023-2024学年九年级下学期3月教学质量检测数学试题原卷版docx、辽宁省抚顺新市抚区2023-2024学年九年级下学期3月教学质量检测数学试题解析版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

考生注意：所有试题必须在答题卡指定区域内作答，在本试卷上作答无效
第一部分 选择题（共30分）
一、选择题（本题共10小题，每小题3分，每题四个选项中，只有一项符合题目要求）
1. 下列食品标识中，既是轴对称图形又是中心对称图形的是（ ）
A. 绿色饮品B. 绿色食品
C. 有机食品D. 速冻食品
2. 反比例函数 图象过点， 则k是（ ）
A. 6B. C. 5D. -5
3. 由大小相同的正方体搭成的几何体如图所示，其左视图是（ ）
A. B. C. D.
4. 在中，，若，则的值为（ ）
A. B. C. D.
5. 春节期间，小澎陪妈妈去爬山，如图，两人从山脚下A处沿坡前行，到达C处时，发现C处标语牌上写着“恭喜你已上升米”，若此山坡的坡度，爱思考的小澎很快告诉妈妈：“我们至少走坡路（ ）米了”．
A. B. C. D.
6. 如图，是的直径，B，D是上的两点，连接，若，则的度数为（ ）

A. B. C. D.
7. 某市举行中学生党史知识竞赛，如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率（该校优秀人数与该校参加竞赛人数的比值）与该校参加竞赛人数的情况，其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上，则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是（ ）
A. 甲B. 乙C. 丙D. 丁
8. 已知二次函数y＝x2﹣6x+1，关于该函数在﹣1≤x≤4的取值范围内，下列说法正确的是（ ）
A. 有最大值8，最小值﹣8B. 有最大值8，最小值﹣7
C. 有最大值﹣7，最小值﹣8D. 有最大值1，最小值﹣7
9. 如图，在下列网格中小正方形的边长均为1，点都在格点上，则的正弦值是（ ）
A. B. C. D.
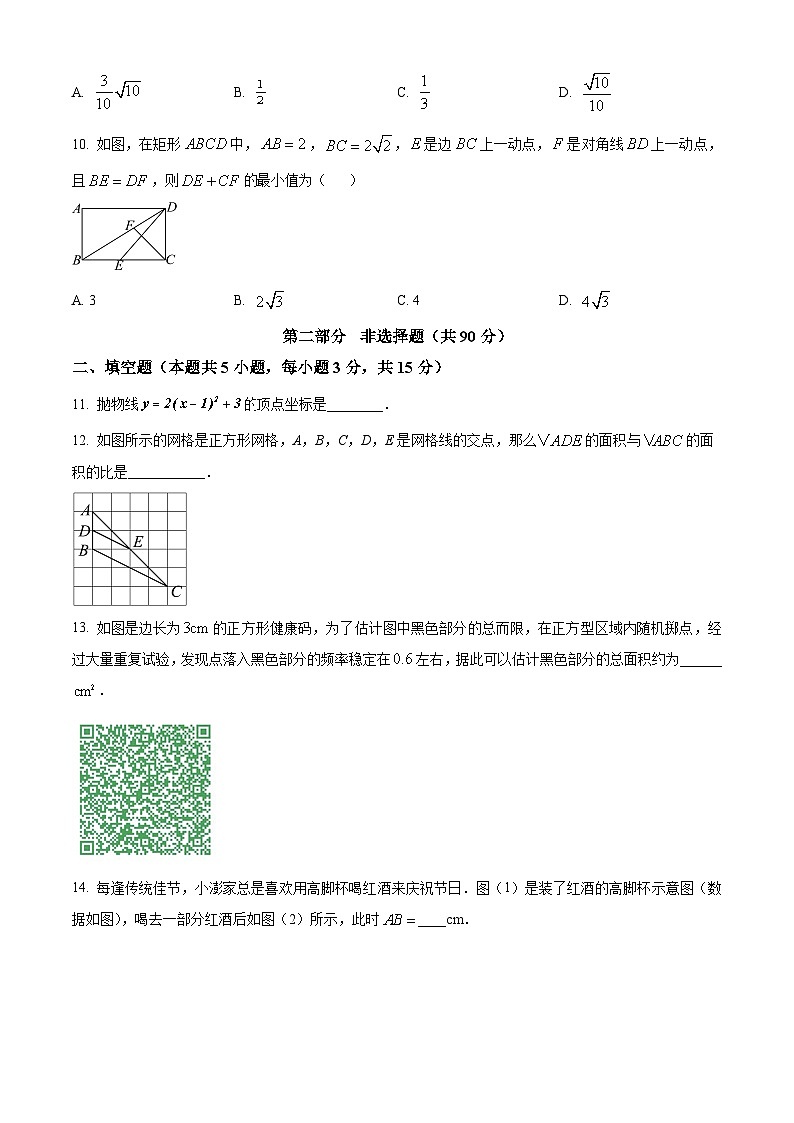
10. 如图，在矩形中，，，是边上一动点，是对角线上一动点，且，则最小值为（ ）
A. 3B. C. 4D.
第二部分 非选择题（共90分）
二、填空题（本题共5小题，每小题3分，共15分）
11. 抛物线顶点坐标是________．
12. 如图所示的网格是正方形网格，A，B，C，D，E是网格线的交点，那么的面积与的面积的比是___________．
13. 如图是边长为的正方形健康码，为了估计图中黑色部分的总而限，在正方型区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在左右，据此可以估计黑色部分的总面积约为______．
14. 每逢传统佳节，小澎家总是喜欢用高脚杯喝红酒来庆祝节日．图（1）是装了红酒的高脚杯示意图（数据如图），喝去一部分红酒后如图（2）所示，此时____cm．
15. 如图，点E是正方形对角线所在直线上一点，点F在的延长线上，连接，过点E作交的延长线于点G，连接并延长交的延长线于点P．若，，当时，则线段的长是______．
三、解答题（第16题6分，第17题10分，共计16分）
16. 计算
（1）2sin30°﹣3tan230°+tan260°；
（2）cs30°﹣sin45°+tan45°•cs60°．
17. 如图，的三个顶点的坐标分别为，，．
（1）以原点O为位似中心，画出的位似图形，使它与的相似比为；
（2）画出的外接圆，写出的外心D的坐标，并计算出弧BC的长．
四、解答题（第18题10分，第19题8分，共18分）
18. 如图，四边形为正方形，点A的坐标为，点B的坐标为，反比例函数的图象经过点C，一次函数的图象经过点C和点A．
（1）求反比例函数与一次函数的解析式；
（2）写出的解集；
（3）点P是反比例函数图象上的一点，若的面积恰好等于正方形的面积的，求P点坐标．
19. 如图，是的直径，点C是的中点，过点C作的切线交的延长线于点E，连接．
（1）求证：；
（2）若，，求半径．
五、解答题（本题8分）
20. 我们的家乡抚顺有美丽的浑河穿城而过，十里滨水公园更是成为市民休闲娱乐的风景带．某数学兴趣小组在一次课外活动中，测量十里滨水公园浑河某段的河宽．如图所示，小组成员选取的点，是桥上的两点，点，，在河岸的同一直线上，且．若，间的距离120米，在点处测得与平行于的直线间的夹角为，在点处测得与直线之间的夹角为，求这段河的宽度．（结果保留到1米，）
六、解答题（本题8分）
21. 已知抛物线与x轴交于点A，B，与y轴交于点C，连接，．
（1）求出点A，C两点的坐标和；
（2）点P是抛物线第一象限上一点，作轴交直线于点Q，若，求点P的坐标．
七、解答题（本题12分）
22. 综合与应用
如果将运动员的身体看作一点，则他在跳水过程中运动的轨迹可以看作为抛物线的一部分．建立如图2所示的平面直角坐标系，运动员从点起跳，从起跳到入水的过程中，运动员的竖直高度与水平距离满足二次函数的关系．
（1）在平时的训练完成一次跳水动作时，运动员甲的水平距离x与竖直高度y的几组数据如下表：
根据上述数据，求出y关于x的关系式；
（2）在（1）这次训练中，求运动员甲从起点A到入水点的水平距离的长；
（3）信息1：记运动员甲起跳后达到最高点B到水面高度为，从到达到最高点B开始计时，则他到水面的距离与时间之间满足．
信息2：已知运动员甲在达到最高点后需要的时间才能完成极具难度的270C动作．
问题解决：
①请通过计算说明，在（1）的这次训练中，运动员甲能否成功完成此动作？
②运动员甲进行第二次跳水训练，此时他的竖直高度与水平距离的关系为，若选手在达到最高点后要顺利完成270C动作，则a的取值范围是______．
八、解答题（本题13分）
23. 探究与实践
【问题初探】
在数学活动课上，老师给出如下问题：
如图①，在正方形中，点N、M分别在边、上，连接、、．若，将绕点A顺时针旋转，点D与点B重合，得到．
易证：，从而得．
【方法归纳】
有公共顶点，锐角等于较大的角的一半时，通过旋转，可将角进行等量转化，构造全等（相似）的三角形的几何模型．这种解法称为经典之旋转法．
【实践探究】
（1）在用图①结论下，若，，则正方形的边长是多少？
（2）如图②，点M、N分别在正方形边、上，且．点E、F分别在、上，，连接，猜想三条线段、、之间满足的数量关系，并说明理由．
【拓展延伸】
（3）如图③，在矩形中，，，点M、N分别在边、上，连接、，已知，，求的长．
水平距离x（m）
0
1
1.5
竖直高度y（m）
10
10
6.25